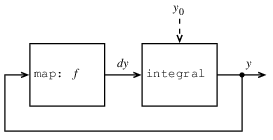
図3.34 方程式dy/dt=f(y)を解く「アナログ計算機の回路」
(define int
(cons-stream initial-value
(add-streams (scale-stream integrand dt)
int)))
このような暗黙の定義を扱う解釈系の能力はcons-streamに組み込まれているdelayに依存している. このdelayがないと, 解釈系はcons-streamの二つの引数を評価する前にintを構成することが出来ない. 引数の評価はintが既に定義されていることを要求する. 一般にdelayはループを含む信号処理システムをストリームを使ってモデル化するのに重要である. delayがないとわれわれのモデルは, 信号処理要素への入力は出力が作られる前に完全に評価されるように形式化しなけばならない. これはループには使えない.
困ったことにループのあるシステムのストリームモデルはcons-stream
に与えられる「隠れた」delayを越えてdelayの使用を要求する. 例えば図3.34はfを与えられた関数として,
微分方程式dy/dt=f(y)を解く信号処理システムを示す. この図で入力信号にfを作用させる写像部品は, こういう式を解くのに実際に使われるアナログ計算機の回路によく似た方法で, フィードバックループの中で積分器に接続されている.

図3.34 方程式dy/dt=f(y)を解く「アナログ計算機の回路」
yの初期値y0が与えられたと仮定すると, 手続き
(define (solve f y0 dt) (define y (integral dy y0 dt)) (define dy (stream-map f y)) y)を使ってこのシステムのモデル化を試みることが出来る. この手続きは, solveの第一行でintegralの呼出しが入力dyが定義されていることを要求するので動かない. 定義はsolveの第二行目まで起きない.
他方, dyを知らずともyストリームを原理的に生成し始めることが出来るので, 定義の意図は筋が通っている. 実際integralや他の多くのストリーム演算は, 引数の部分的な情報を与えられて答の一部を生成出来るという点で, cons-streamに似た性質を持つ. integralでは, 出力ストリームの第一要素は指定されたinitial-valueである. このように被積分値dyを評価することなしに, 出力ストリームの第一要素を生成することが出来る. 一旦yの第一要素が分れば, solveの第二行のstream-mapはdyの第一要素を生成するため働き始めることが出来, dyはyの次の要素を生じ, それが続く.
この考えを利用し, integralを再定義し, 被積分ストリームが 遅延引数(delayed argument)と思う. integralは出力ストリームの第一要素より先を生成するよう要求された時だけ, 被積分値を評価すべくforceする:
(define (integral delayed-integrand initial-value dt)
(define int
(cons-stream initial-value
(let ((integrand (force delayed-integrand)))
(add-streams (scale-stream integrand dt)
int))))
int)
yの定義の中のdyの評価を遅延させることで, solve手続きを実装出来る:71
(define (solve f y0 dt) (define y (integral (delay dy) y0 dt)) (define dy (stream-map f y)) y)一般に, integralの呼出し側は, 被積分引数をdelayしなければならない. y(0)=1をその初期値とする微分方程式dy/dt=yの解のy=1での値を計算し, e ≈ 2.718の近似を得ることで, solve手続きが実証出来る:
(stream-ref (solve (lambda (y) y) 1 0.001) 1000) 2.716924
(define (integral integrand initial-value dt)
(cons-stream initial-value
(if (stream-null? integrand)
the-empty-stream
(integral (stream-cdr integrand)
(+ (* dt (stream-car integrand))
initial-value)
dt))))
ループのあるシステムで使うと, この手続きにはintegralの初版と同じ問題がある. この手続きを修正し,
integrandを遅延引数としてとり, 上のsolve手続きで使えるようにせよ.
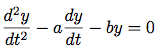
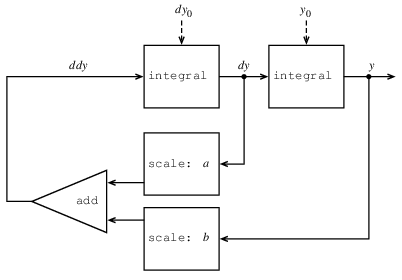
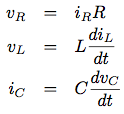
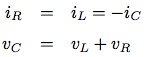
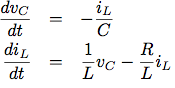
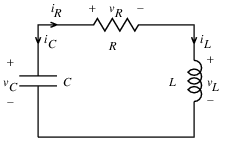
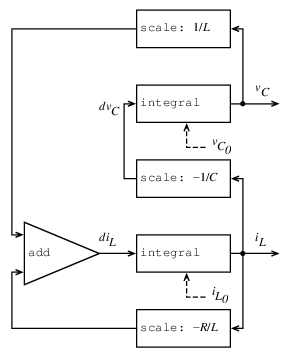
引数として回路のパラメタR, LおよびCと, 時間増分dtをとる手続きRLCを書け. 問題3.73のRC手続きと同様に, RLCは状態変数vC0とiL0の初期値をとり, 状態vCとiLのストリームの対(consを使う)を生じる手続きを生じるものとする. このRLCを使って,
R=1オーム, C=0.2ファラド, L=1ヘンリ, dt=0.1秒, 初期値iL0=0アンペア,
vC0=10ボルトの直列RLC回路の振舞いをモデル化する一対のストリームを生成せよ.
二つの異るクラスの手続きが必要になるのを避ける一つの方法は, すべての手続きが遅延引数をとるようにすることである. 手続きのすべての引数が自動的に遅延になり,本当に必要になった時(例えば基本演算が要求する時)にだけ強制される評価モデルを採用することが出来る. これはわれわれの言語を,
1.1.5節で評価の置換えモデルを話した時に述べた, 正規順序の評価を使うよう変更することだ. 正規順序への変更は, 遅延評価の使用を単純化する一様で優美な方法を提供し, ストリーム処理だけに関心があるのなら, 採用すべき自然の戦略である. 4.2節で, 評価器を学んだ後, このように言語を変換する方法を見ることにする. 困ったことに, 手続き呼出しに遅延を含ませることは,
代入を利用し, データを更新し, 入力, 出力を実行するような, 事象の順に依存するプログラムを設計する力を台無しにする. cons-streamの単一のdelayでさえ, 問題3.51や3.52に見るような大きな混乱をもたらす. 誰もが知っているように, 変更と遅延評価はプログラム言語ではうまく混ざらず,
これら二つを同時に扱う方法を工夫するのは, 研究の盛んな領域である.
71
ある実装ではこれが働くような単純な変更があるかも知れないが, この手続きはすべてのScheme実装で働くとは保証されない. 問題はSchemeの実装が内部定義を扱う方法の微妙な違いをどうにかしなければならないことにある. (問題4.1.6参照)
72
Pascalのような普通の強い型つけの言語が,
高階手続きで対処しなければならない困難さのLispへのささいな反映である. そういう言語では, プログラマは, 各手続きで, 数値, 論理値, 並びなど,
引数と結果のデータ型を指定しなければならない. 従ってstream-mapのような単一の高階手続きを使い, 「与えられた手続きprocで, 並びのすべての要素を写像する」とういような抽象を表現することは出来ない. そうではなく, procとして指定する引数と結果のデータ型の, 異る組合せ毎に異る写像手続きを必要とする. 高階手続きの面前で「データ型」の実用的な考えを維持しようとすると多くの困難な問題が起きる. この問題を扱う一つの方法は言語
ML
(Gordon,
Milnerおよび
Wadsworth 1979)によって示された. その「ポリモルフィックデータ型」はデータ型間の高階の変換の雛型を含んでいる. その上MLの殆んどの手続きのデータ型はプログラマによって明示的には宣言されない. そうではなく, MLは
型推論(type inference)機構を持ち, 環境の情報を使って新しく定義した手続きのデータ型を推論する.