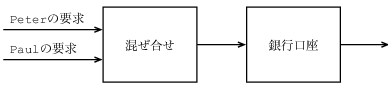
図3.38 取引き要求の二つのストリームの混合せでモデル化した共同銀行口座
鍵となる部品化の論点は, 乱数を使うプログラムから, 乱数発生のための内部状態を隠したいということだ. 手続きrand-updateから始めた. その順次の値は乱数の補給を担当し, これを乱数発生器を作るのに使った:
(define rand
(let ((x random-init))
(lambda ()
(set! x (rand-update x))
x)))
ストリームの形式化では, 乱数発生器それ自身は存在せず, rand-updateを次々と呼び出して作られた乱数のストリームがあるだけである:
(define random-numbers
(cons-stream random-init
(stream-map rand-update random-numbers)))
これをrandom-numbersストリームの相続く対で実施した, Cesàro実験の出力ストリームを構成するのに使う:
(define cesaro-stream
(map-successive-pairs (lambda (r1 r2) (= (gcd r1 r2) 1))
random-numbers))
(define (map-successive-pairs f s)
(cons-stream
(f (stream-car s) (stream-car (stream-cdr s)))
(map-successive-pairs f (stream-cdr (stream-cdr s)))))
cesaro-streamはmonte-carlo手続きに与えられ, それは確率の見積りのストリームを作り出す. 次にその結果は, πの見積りのストリームへと変換される. プログラムのこの版は, 試行を何回行うかを示すパラメタはもはや必要としない. piストリームを先の方まで眺めると, (より多くの実験から)πのよりよい見積りが得られる:
(define (monte-carlo experiment-stream passed failed)
(define (next passed failed)
(cons-stream
(/ passed (+ passed failed))
(monte-carlo
(stream-cdr experiment-stream) passed failed)))
(if (stream-car experiment-stream)
(next (+ passed 1) failed)
(next passed (+ failed 1))))
(define pi
(stream-map (lambda (p) (sqrt (/ 6 p)))
(monte-carlo cesaro-stream 0 0)))
この解決法には, 任意の実験を扱う一般的なmonte-carlo手続きを形式化出来るので, かなりの部品化度がある. しかも代入も局所状態もない.
ストリームが局所状態を持つオブジェクトをモデル化するもう一つの方法を提供することを見てきた. あるオブジェクトの局所状態のような変りゆく量を, 順次の状態の時間的歴史を表現するストリームを使ってモデル化する. 要するにストリームを使って時を明確に表現し, シミュレート中の時を評価中に起きる事象の並びから切り離す. 実際delayが存在するので, モデルのシミュレートされた時と評価中の事象の順の間にはあまり関係がない.
モデル化のこの二つの解決法を対比するため, 銀行口座の残高をモニターする 「払出し処理器」の実装を考え直そう. 3.1.3節でそのような処理器の単純化版を実装した:
(define (make-simplified-withdraw balance)
(lambda (amount)
(set! balance (- balance amount))
balance))
make-simplified-withdrawの呼出しは計算オブジェクトを作り, そのそれぞれはオブジェクトの順次の呼出しで減少する局所状態変数balance
を持っている. オブジェクトは引数としてamountをとり, 新しい残高を返す. 銀行口座の利用者がそういうオブジェクトへの一連の入力を入力し, スクリーンに映される一連の出力の値を眺めているのを想像することが出来る.
また別に, 払出し処理器を, 入力として残高と払出し額のストリームをとり, 口座の順次の残高のストリームを作る手続きでモデル化することも出来る:
(define (stream-withdraw balance amount-stream)
(cons-stream
balance
(stream-withdraw (- balance (stream-car amount-stream))
(stream-cdr amount-stream))))
stream-withdrawは出力が入力によって完全に決定される, 明確に定義された数学的関数を実装する. しかし入力\linebreakamount-streamが,
利用者が入力した順次の値のストリームであり, 結果としての残高のストリームが表示されているとしよう. すると値を入力し, 結果を眺めている利用者の見え方からは, ストリーム処理はmake-simplified-withdrawで作り出されたオブジェクトと同じ振舞いをする. ところがストリーム版には代入も局所状態変数もない.
従って3.1.3節で直面した理論的困難は一つもない. しかもシステムには状態が存在する.
これは実に注目すべきことだ. stream-withdrawが, その振舞いが変化しない, 明確に定義された数学的関数を実装したとしても, ここでの利用者の認識は, 変化する状態を持つシステムと対話しているという認識である. この矛盾を解く一つの方法は, システムに状態を持たせるのは, 利用者の時間的存在であると認めることである. 利用者が対話から一歩下って個々の取引きではなく, 残高のストリームを使って考えるとすれば, システムは状態なしに見えてくる.73
複雑なプロセスの一部の視点からは, 他の部分は時とともに変化するように見える. それは時間変化する隠れた局所状態を持つ. (その世界の一部としての視点から世界を見るように)計算機内の構造を使い, このような世界の自然な分解をモデル化するプログラムを書こうとするなら, 時とともに変化しなければならない---関数的でない計算オブジェクトを作ることになる. われわれは状態を局所状態変数でモデル化し, 状態変化をこれらの変数への代入でモデル化する. こうすることで, 計算モデルの実行時間を, われわれがその一部である世界の時間にし, 計算機の中に「オブジェクト」が出来るのである.
主としてこれがわれわれがその一部である世界との対話の認識に合っているため, オブジェクトによるモデル化は強力で直観的である. しかし本章で繰り返し見たように, これらのモデルは事象の順序の制約と, 複数のプロセスの同期という困難な問題を惹き起す. この問題の回避の可能性は, 代入と可変データの用意を持たない 関数型プログラム言語(functional programming language)の開発を促進して来た. そういう言語では, すべての手続きは振舞いが変化せず, 引数で明確に定義された数学的関数を実装する. 関数型による解決法は並列システムを扱うのに極めて魅力的である. 74
他方, よく見ると, 時に関係ある問題も関数型モデルに近づきつつあることが分る. 特に厄介な領域は, われわれが対話的システム, それも独立な実体間の対話をモデル化するシステムを設計する時に発生する. 例えばもう一度共同口座を認める銀行システムの実装を考えよう. 代入とオブジェクトを使う通常のシステムでは, 3.1.3節で見たように, PeterとPaulが取引きの要求を同一の銀行口座オブジェクトへ送ることで, 二人は口座を共有するという事実をモデル化する. 「オブジェクト」そのものが存在しないストリームの観点からは,取引き要求のストリームに操作して, 応答のストリームを生じるプロセスとして, 銀行口座はモデル化出来ると表明してきた. 従ってPeterとPaulが,
共同銀行口座を持つという事実は, Peterの取引き要求のストリームをPaulの取引き要求ストリームと混ぜ合せ, 図3.38に示すように, その結果を銀行口座ストリームへ送り込むことでモデル化出来る.

図3.38 取引き要求の二つのストリームの混合せでモデル化した共同銀行口座
この形式化の問題は, 混合せ(merge)の考え方にある. それは単にPeterからの一つの要求とPaulからの一つの要求を交互にとって, 二つのストリームを混ぜ合せるのではない. Paulが口座を殆んどアクセスしなかったとしよう. Paulが口座にアクセスするまで, Peterに次の取引きの発生を待たせるわけにはいかない. 混合せをどのように実装しても, PeterとPaulが会った時, ある取引きは会う前に処理され, 別の取引きはその会った後で処理されたことに合意出来るという意味で, PeterとPaulが認知する「実時間」に制約された, 何らかの方法で二つの取引きストリームを混ぜ合せなければならない. 75 これは3.4.1節で扱わなければならなかったのと全く同じ制約である. そこでは, 状態を持つオブジェクトの並列処理で, 事象の「正しい」順序を保証するのに, 明確な同期を導入する必要を見た. このように, 関数型スタイルを支援しようとすると, 異るエージェントからの入力を混ぜ合せる必要は, 関数型スタイルを除去するという, 同じ問題を再導入する.
本章は, モデル化しようとする実世界の認識に合致する構造を持つ, 計算モデルを構築するという目的をもって始めた. われわれは, ばらばらで, 時に縛られ, 相互作用する, 状態を持つオブジェクトの集りで世界をモデル化することも出来るし, また単一の, 時に縛られない, 状態のない個体で世界をモデル化することも出来る. どちらの見方も強力な利点があるが, どちらかだけでは完全には満足出来ない. もっとすばらしい統合が現れなければならない.
76
73
物理学でも同様で, 動いている粒子を観測する時, われわれは粒子の位置(状態)は変化しているという. しかし, 粒子の時間空間の
世界線の視点からは, 変化はない.
74
Fortranの発明者
John Backusは1978年のACM Turing賞を受賞した時, 関数型プログラミングを高く称賛した. 受賞講演(Backus 1978)は関数型解決法を強く奨励した. 関数型プログラミングの優れた解説は,
Henderson 1980,
Darlington,
Hendersonおよび
Turner 1982にある.
75
任意の二つのストリームがあり, 一般に受入れ可能な混合せの順が複数あることに注意しよう.
従って「混合せ」は技術的には関数というより関係である. ---答は入力の決定的な関数ではない. すでに述べたように(脚注39)並列性を扱う時, 非決定性は本質的である. 混合せの関係は, 関数的見方からは, 同じく本質的な非決定性を示す. 4.3節で更に別な観点から非決定性を見よう.
76
オブジェクトモデルは, 世界をばらばらな部品に分割することで, それを近似する. 関数型モデルは
オブジェクトの境界に沿っての部品化はしない. オブジェクトモデルは「オブジェクト」の非共有の状態が, 共有の状態よりずっと大きい場合に有用である.
オブジェクトの視点が失敗する場所の例は,
量子力学で, そこでは物を個々の粒子と考えると矛盾と混乱に陥る. オブジェクトの視点と関数的視点の統合は, プログラミングより基本的認識論に見るべきものがある.