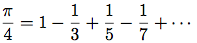
最初に級数の被加数(符号が交互になる奇数の逆数)のストリームを生成する. 次に(問題3.55のpartial-sums手続きを使い)更に多くの項の和のストリームを作り, 結果を4倍する:
ストリームによる問題解決は, 状態変数への代入の周囲に組織化されたシステムとは異る部品化の境界を持つシステムが構築出来るため, 照り輝く. 例えば各時点での状態変数の値ではなく, 全時系列(または信号)を関心の対象として考えることが出来る. これにより, 異る時点の状態の要素を組み合せたり比較したりするのが便利になる.
(define (sqrt-improve guess x) (average guess (/ x guess)))
元々のsqrtの手続きでは, これらの予測値を状態変数の順次の値とした. そうではなく最初の予測値1から始る, 予測値の無限のストリームが生成出来る:65
(define (sqrt-stream x)
(define guesses
(cons-stream 1.0
(stream-map (lambda (guess)
(sqrt-improve guess x))
guesses)))
guesses)
(display-stream (sqrt-stream 2))
1.
1.5
1.4166666666666665
1.4142156862745097
1.4142135623746899
...
更によい予測値を得るため, ストリームの次々の項が生成出来る. 希望するなら, 答が十分良好になるまで, 項を生成し続ける手続きも書ける. (問題3.64参照)
同様に扱えるもう一つの反復は, 1.3.1節でみた交代級数に基づくπの近似値の生成である:
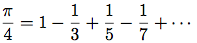
最初に級数の被加数(符号が交互になる奇数の逆数)のストリームを生成する. 次に(問題3.55のpartial-sums手続きを使い)更に多くの項の和のストリームを作り, 結果を4倍する:
(define (pi-summands n)
(cons-stream (/ 1.0 n)
(stream-map - (pi-summands (+ n 2)))))
(define pi-stream
(scale-stream (partial-sums (pi-summands 1)) 4))
(display-stream pi-stream)
4.
2.666666666666667
3.466666666666667
2.8952380952380956
3.3396825396825403
2.9760461760461765
3.2837384837384844
3.017071817071818
...
近似は緩やかに収束するが, これはπの次第に改善される近似のストリームを与える. 並びの八項でπの値は3.284と3.017の間に押えられる.
これまでは, 状態のストリームの使い方は, 状態変数の更新とあまり違わない. しかしストリームには面白いトリックをする機会がある. 例えばストリームを 並び加速(sequence accelerator)で変換し, 近似の並びを, 元々のと同じ値にずっと速く収束する新しい並びに変更することが出来る.
そういう加速の一つは十八世紀, スイスの数学者
Leonhard Eulerによるもので, 交代級数(項の符号が交互になる級数)の部分和である並びにうまく働く. Eulerの技法では, Snを元々の和の並びのn番目の項とすると, 加速される並びは
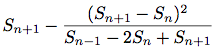
の項を持つ. つまり元々の並びが値のストリームで表現されているなら, 変換された並びは
(define (euler-transform s)
(let ((s0 (stream-ref s 0)) ; Sn-1
(s1 (stream-ref s 1)) ; Sn
(s2 (stream-ref s 2))) ; Sn+1
(cons-stream (- s2 (/ (square (- s2 s1))
(+ s0 (* -2 s1) s2)))
(euler-transform (stream-cdr s)))))
Euler加速をπの近似の並びで見ることが出来る:
(display-stream (euler-transform pi-stream)) 3.166666666666667 3.1333333333333337 3.1452380952380956 3.13968253968254 3.1427128427128435 3.1408813408813416 3.142071817071818 3.1412548236077655 ...
更に良好にするため, 加速された並びを加速し, それのまた再帰的な加速が続けられる. つまりストリームのストリーム (タブロー(tableau)という構造)を作り出し, そこでは各ストリームは直前のものの変換である:
(define (make-tableau transform s)
(cons-stream s
(make-tableau transform
(transform s))))
タブローは
(define (accelerated-sequence transform s)
(stream-map stream-car
(make-tableau transform s)))
πの並びのこの種の「超加速」を示すことが出来る:
(display-stream (accelerated-sequence euler-transform
pi-stream))
4.
3.166666666666667
3.142105263157895
3.141599357319005
3.1415927140337785
3.1415926539752927
3.1415926535911765
3.141592653589778
...
結果は印象的だ. 並びの八項をとるとπの14桁の正しい値が得られる. 元々のπの並びだけを使ったらこの大きさの精度を得るには1013の程度の項の計算を必要とする(つまり級数を各項が10-13より小さくなるまで展開する.)
ストリームを使わないでもこういう加速法を実装出来たかも知れない. しかしストリームの形式化は, 状態の全体の並びが, 一様な演算の組で操作出来るデータ構造として使えるので, 特に美しく, 便利である.
問題 3.63
Louis Reasonerは, sqrt-stream手続きは局所変数guessesを使わず, 次のように直截な方法で書けなかったかと質問した.
(define (sqrt-stream x)
(cons-stream 1.0
(stream-map (lambda (guess)
(sqrt-improve guess x))
(sqrt-stream x))))
Alyssa P. Hackerは手続きのこの版は, 冗長な計算をするので, かなり非効率だと答えた. Alyssaの答を説明せよ. delayの実装が,
memo-proc(3.5.1節)の用意した最適化を使わず(lambda ()
⟨exp⟩)だけを使ったとしたら, 二つの版の効率に違いはあるか.
(define (sqrt x tolerance) (stream-limit (sqrt-stream x) tolerance))により, 平方根を与えられた許容誤差まで計算出来る.
例えば2.2.3節のprime-sum-pairs手続きを一般化し, i ≤ jで, i + jが素数である, すべての整数(i, j)の対のストリームが作りたかったとしよう. int-pairsが i ≤ jなる整数$(i, j)のすべての対の並びなら, 要求されたストリームは単に
(stream-filter (lambda (pair)
(prime? (+ (car pair) (cadr pair))))
int-pairs)
である.66
そうするとわれわれの問題は, ストリームint-pairsを作ることである.
より一般的には二つのストリームS = (Si)とT = (Tj)があるとし,無限の正方配列
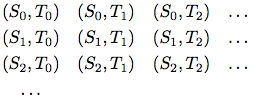
を考える. この配列の対角線上か対角線より上にある対のすべて, つまり対
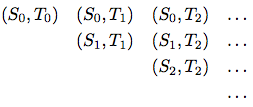
を含むストリームが作りたい. (SとTが整数のストリームだとすれば, これが望みのストリームint-pairsである.)
対の一般的なストリームを(pairs S T)と呼び, それが三つの部分: 対(S0, T0), 第一行の残りの対, および残りの対から出来ているとする:67

この分解の三番目のもの(第一行に入らない対)は(再帰的に)
(stream-cdr S)と(stream-cdr T)から作られた対であることに注意しよう. また第二部(第一行の残り)は
(stream-map (lambda (x) (list (stream-car s) x))
(stream-cdr t))
に注意する. そこで対のストリームを次のように作ることが出来る.
(define (pairs s t)
(cons-stream
(list (stream-car s) (stream-car t))
(⟨何らかの方法で組み合わせる⟩
(stream-map (lambda (x) (list (stream-car s) x))
(stream-cdr t))
(pairs (stream-cdr s) (stream-cdr t)))))
手続きを完成するために, 二つの内部ストリームを組み合せる何らかの方法を選ぶ必要がある. 一つの考えは2.2.1節のappend手続きに似たストリーム版を使うことである:
(define (stream-append s1 s2)
(if (stream-null? s1)
s2
(cons-stream (stream-car s1)
(stream-append (stream-cdr s1) s2))))
しかしこれは, 第二のストリームを取り込む前に, 第一のストリームからすべての要素をとるので, 無限ストリームには不適当である. 特に(pairs integers integers)を使い, 正の整数のすべての対を生成しようとする時, 結果のストリームは, 最初の整数が1に等しいすべての対を作ろうとし, それ以外の値を最初の整数とする対は決して作られない.
無限のストリームを扱うには, プログラムを十分長く走らせると, すべての要素に遂にはたどり着けるということが確かな組合せの順を考える必要がある. これを達成する優美な方法は次のinterleave手続きを使うものである:68
(define (interleave s1 s2)
(if (stream-null? s1)
s2
(cons-stream (stream-car s1)
(interleave s2 (stream-cdr s1)))))
interleaveは二つのストリームから要素を交互にとるので, 第一のストリームが無限であっても, 第二のストリームのすべての要素は, いつかは混ぜ合されたストリームへ行く道を見つける.
要求された対のストリームは
(define (pairs s t)
(cons-stream
(list (stream-car s) (stream-car t))
(interleave
(stream-map (lambda (x) (list (stream-car s) x))
(stream-cdr t))
(pairs (stream-cdr s) (stream-cdr t)))))
のように生成出来る.
(define (pairs s t)
(interleave
(stream-map (lambda (x) (list (stream-car s) x))
t)
(pairs (stream-cdr s) (stream-cdr t))))
これは動くか. Louisのpairsの定義を使って(pairs integers integers)を評価すると, 何が起きるか考えよ.
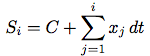
(define (integral integrand initial-value dt)
(define int
(cons-stream initial-value
(add-streams (scale-stream integrand dt)
int)))
int)
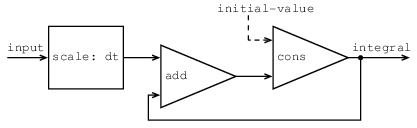
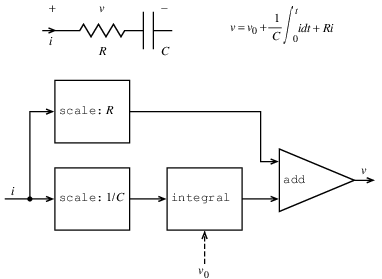
この回路をモデル化する手続きRCを書け. RCは入力としてR,
Cとdtの値をとり, 入力として電流iを表現するストリームとキャパシタの電圧の初期値v0をとり, 出力として電圧vのストリームを返す手続きを返すものとする. 例えば(define RC1 (RC 5 1 0.5))を評価することでR
= 5オーム, C = 1ファラド, 0.5秒の時間間隔のRC回路をモデル化するのにRCが使えなければならない. これは電流の時系列を表すストリームキャパシタの初期電圧をとり, 電圧の出力ストリームを生じる手続きとしてRC1を定義する.
問題 3.74
Alyssa P. Hackerは物理的検出器からの信号を処理するシステムを設計している. 彼女が作ろうとしている一つの重要な機能は, 入力信号の零交差
(zero crossing)を記述する信号である. つまり結果の信号は, 入力信号が負から正に変った時は+1, 入力信号が正から負へ変った時は-1, それ以外は0とする. (0入力の符号は正と仮定する.) 例えば典型的な入力信号と対応する零交差信号は
... 1 2 1.5 1 0.5 -0.1 -2 -3 -2 -0.5 0.2 3 4 ... ... 0 0 0 0 0 -1 0 0 0 0 1 0 0 ...となる. Alyssaのシステムでは検出器からの信号はストリーム sense-dataで表現され, ストリームzero-crossingsが対応する零交差のストリームである. Alyssaはまず手続きsign-change-detectorを書いた. これは引数として二つの値をとり, それらの値の符号を比較し, 適切な0, 1または-1を生じる. 彼女はそれから零交差ストリームを次のように構成した.
(define (make-zero-crossings input-stream last-value)
(cons-stream
(sign-change-detector (stream-car input-stream) last-value)
(make-zero-crossings (stream-cdr input-stream)
(stream-car input-stream))))
(define zero-crossings (make-zero-crossings sense-data 0))
Alyssaの上司のEva Lu Atorは通りかかり, このプログラムは問題3.50のstream-mapの一般化した版を使う次のと大体同じだといった:
(define zero-crossings (stream-map sign-change-detector sense-data ⟨expression⟩))⟨expression⟩を補ってプログラムを完成せよ.
(define (make-zero-crossings input-stream last-value)
(let ((avpt (/ (+ (stream-car input-stream) last-value) 2)))
(cons-stream (sign-change-detector avpt last-value)
(make-zero-crossings (stream-cdr input-stream)
avpt))))
これはAlyssaの計画を正しくは実装していない. Louisが入れた虫を見つけ,
プログラムの構造を変えずに修正せよ. (ヒント: make-zero-crossingsの引数の個数を増やす必要がある.)
65
内部変数guessesを束縛するletは, guessesの値はguessesそれ自身に依存するので, 使えない. 問題3.63は, なぜ局所変数が必要かを考える.
66
2.2.3節のように, 整数の対をLispの対ではなく, リストで表現する.
67
なぜこういう分解を選んだかは問題3.68に洞察があるのを見よ.
68
組合せの順に関して要求される性質の正確な表現は次の通り: 第一のストリームの要素iと, 第二のストリームの要素jに対応する対が, 出力ストリームのf(i,j)番目現れるような二引数関数fが存在すべきである. これを達成すべく, interleaveを使うトリックは, それを言語
KRC(Turner 1981)で使った
David Turnerによって示された.
69
重み関数には, 対の配列の行を右へ, 並びを下へ進むに従い,対の重みが増えるよう, 要求する.
70
HardyのRamanujan追悼文(Hardy 1921)から引用すると「『すべての正の整数は彼の友人であった』といったのはLittlewoodだった(と思う.) 彼がパトニーで療養していた時, 見舞いにいったのを覚えている. 1729番というタクシーに乗ったので, その数には何の面白味もないといい, それが悪い予兆でないことを望むといった. 『いや』彼は答えた『それは非常に興味のある数だ. それは二通りで二つの立方数の和で表現出来る最小の数だ』」. 重みつきの対を使ってRamanujan数を作るトリックは
Charles Leisersonが示した.