(define (integers-starting-from n) (cons-stream n (integers-starting-from (+ n 1)))) (define integers (integers-starting-from 1))integersはcarが1で, cdrが2で始る整数を生じる約束の対だから, これはまともである. これは無限に長いストリームであるが, いつでもその有限な部分だけを調べることが出来る. そこでわれわれのプログラムは, 無限のストリームがそこに存在しないことは知らない.
integersを使うと, 他の無限ストリーム, 例えば7で割り切れない整数のストリームのようなものを定義出来る:
(define (divisible? x y) (= (remainder x y) 0))
(define no-sevens
(stream-filter (lambda (x) (not (divisible? x 7)))
integers))
するとこのストリームの要素にアクセスすることで, 7で割り切れない整数を見つけることが出来る:
(stream-ref no-sevens 100) 117
integersとの類推で, Fibonacci数の無限のストリームが定義出来る:
(define (fibgen a b) (cons-stream a (fibgen b (+ a b)))) (define fibs (fibgen 0 1))fibsはそのcarが0, cdrが(fibgen 1 1)を評価する約束の対である. この遅延した(fibgen 1 1)を評価すると, それは carが1, cdrが(fibgen 1 2)を評価する約束の対を生じ, このように続く.
もっと衝撃的な無限ストリームを見るため, no-sevensの例を一般化し, Eratosthenesの篩(sieve of Eratosthenes)として知られる方法を使い, 素数の無限ストリームを作る.60 まず最初の素数である2から始る整数で開始する. 残りの素数を得るため, 残りの整数から2の倍数をフィルタする. 3から始るストリームが残る. 3は次の素数である. このストリームの残りから, 3の倍数をフィルタする. すると5から始るストリームが残り, 5は次の素数である. これを続ける. いい替えれば, 素数を次に述べる篩のプロセスで構成する: ストリームSを篩うには, 最初の要素がSの最初の要素であり, 残りがSの残りをSの最初の要素の倍数をフィルタし, 結果を篩って得られるストリームを作る. このプロセスはストリーム演算ですぐ書くことが出来る:
(define (sieve stream)
(cons-stream
(stream-car stream)
(sieve (stream-filter
(lambda (x)
(not (divisible? x (stream-car stream))))
(stream-cdr stream)))))
(define primes (sieve (integers-starting-from 2)))
ある素数を見つけるには, それを尋ねるだけでよい.
(stream-ref primes 50) 233
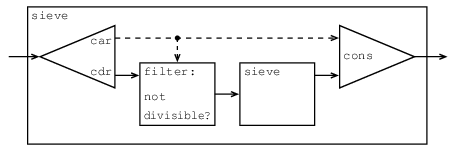
図3.31 「Henderson図」で示すsieveで設定された信号処理系を眺めると面白いことが分る.61 入力ストリームはストリームの最初と残りを分離する「逆cons器」へ送られる. 第一の要素は整除可能のフィルタを構成するのに使う. そのフィルタを残りが通過し, フィルタの出力はもう一つの篩の箱へ送られる. 元々の最初の要素は, 内部の篩の出力とconsされ, 出力ストリームが出来る. このようにストリームが無限なだけでなく, 篩がその中に篩を含んでいる故, 信号処理も無限である.
(define ones (cons-stream 1 ones))これは再帰的手続きの定義のように働く: onesはそのcarが1で, そのcdrがonesを評価する約束の対である. cdrの評価は再び1とonesを評価する約束の対を返し, これが続く.
与えられた二つのストリームの要素毎の和を生じるadd-streamsのような演算でストリームを操作すると, 更に面白いことが出来る:62
(define (add-streams s1 s2) (stream-map + s1 s2))integersを次のように定義出来る:
(define integers (cons-stream 1 (add-streams ones integers)))integersを第一要素が1で, 残りはonesとintegersの和であるストリームと定義している. そこでintegersの第二要素は1足すintegersの第一要素, つまり2; integersの第三要素は1足す integersの第二要素, つまり3; と続く. この定義はintegersストリームの十分なだけがいつでも生成されていて, 次の整数を生じる定義へフィードバック出来るのでうまく働く.
Fibonacci数を同じスタイルで定義出来る:
(define fibs
(cons-stream 0
(cons-stream 1
(add-streams (stream-cdr fibs)
fibs))))
この定義は, fibsは0と1で始るストリームで, ストリームの残りは
fibsを, 一個シフトした自分に足して生成出来るという:
scale-streamはこういうストリーム定義を作るもう一つの有用な手続きである. これはストリームの各要素に与えられた定数を掛ける:
(define (scale-stream stream factor) (stream-map (lambda (x) (* x factor)) stream))例えば
(define double (cons-stream 1 (scale-stream double 2)))は2のべき乗のストリーム: 1, 2, 4, 8, 16, 32, ... を生じる.
素数のストリームのもう一つの定義は, 整数列から始め, それを素数性のフィルタでテストして得られる. 出発するのに最初の素数2を必要とする:
(define primes (cons-stream 2 (stream-filter prime? (integers-starting-from 3))))この定義はnが素数かどうかを, nを
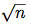 に等しいかより小さい(整数ではなく)素数での整除可能性でテストするので, 見かけほど簡明ではない:
に等しいかより小さい(整数ではなく)素数での整除可能性でテストするので, 見かけほど簡明ではない:
(define (prime? n)
(define (iter ps)
(cond ((> (square (stream-car ps)) n) true)
((divisible? n (stream-car ps)) false)
(else (iter (stream-cdr ps)))))
(iter primes))
primesはprime?述語を使って定義してあり, prime?は
primesストリームを使うので, これは再帰的定義である. この手続きが働く理由は, 次に素数性をチェックしようとする数に対して, いつでもテストするのに十分なだけのprimesストリームが生成されているからである. つまり,
素数性をテストしようとするあらゆるnに対して, nは素数でないか(この場合, nを割り切る素数は既に生成されている.) nは素数であるか(この場合, 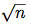 より大きい素数---nよりは小さい---が生成されている.)である.63
より大きい素数---nよりは小さい---が生成されている.)である.63
(define s (cons-stream 1 (add-streams s s)))で定義するストリームの要素を述べよ.
(define factorials (cons-stream 1 (mul-streams ⟨??⟩ ⟨??⟩)))
(define (merge s1 s2)
(cond ((stream-null? s1) s2)
((stream-null? s2) s1)
(else
(let ((s1car (stream-car s1))
(s2car (stream-car s2)))
(cond ((< s1car s2car)
(cons-stream s1car (merge (stream-cdr s1) s2)))
((> s1car s2car)
(cons-stream s2car (merge s1 (stream-cdr s2))))
(else
(cons-stream s1car
(merge (stream-cdr s1)
(stream-cdr s2)))))))))
すると要求されたストリームはmergeを使い, 次のように構成出来る.
(define S (cons-stream 1 (merge ⟨??⟩ ⟨??⟩)))上の⟨??⟩ で記された場所の欠けた式を補え.
(define (expand num den radix) (cons-stream (quotient (* num radix) den) (expand (remainder (* num radix) den) den radix)))(quotientは二つの整数の, 整数の商を返す基本関数である.) (expand 1 7 10)が次々と生じる要素は何か. (expand 3 8 10)は何を生じるか.
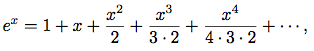
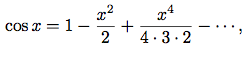
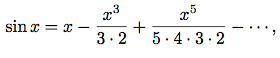
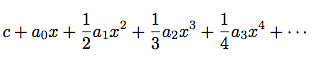
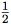 a1,
a1, 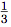 a2, ... を返す手続き
integrate-seriesを定義せよ.
a2, ... を返す手続き
integrate-seriesを定義せよ.  exは自分と同じ微分を持つ. つまりexとexの積分は, e0 = 1の定数項を除いて同じ級数である. 従ってexの級数を
exは自分と同じ微分を持つ. つまりexとexの積分は, e0 = 1の定数項を除いて同じ級数である. 従ってexの級数を(define exp-series (cons-stream 1 (integrate-series exp-series)))で生成出来る. 正弦の微分が余弦であり, 余弦の微分が正弦の符号を変えたものであるという事実から出発し, 正弦と余弦の級数を生成する方法を示せ.
(define cosine-series (cons-stream 1 ⟨??⟩)) (define sine-series (cons-stream 0 ⟨??⟩))
(define (mul-series s1 s2) (cons-stream ⟨??⟩ (add-streams ⟨??⟩ ⟨??⟩)))この手続きは問題3.59の級数を使い, sin2x + cos2 x = 1を確認することでテスト出来る.
60
Eratosthenesは紀元前三世紀のアレキサンドリアギリシャの哲学者で,
地球の周囲の長さを初めて正確に測ったので有名である. 夏至の日の正午の影を観測して計算した. Eratosthenesの篩は, 古典的ではあるが, 特別目的のハードウェア「篩」の基礎を作った. それは最近まで大きな素数を探す, 存在する最も強力な道具であった. 70年代からはしかし, 1.2.6節で論じた
統計的技法の発展で置き換えられている.
61
ストリーム処理を考える方法として, こういう図を初めて書いた
Peter Hendersonから名づけた. 実線は転送される値のストリームを表現する.
carからconsとfilterへの破線はストリームではなく, 一個の値であることを示す.
62
これは問題3.50のstream-mapの一般化版を使う.
63
最後の点は微妙で, pn+1 ≤ pn2という事実による.
(pkはk番目の素数を表す.) このような見積りは達成が非常に難しい.
Euclidによる素数が無限に存在するという古典的な証明は, pn+1 ≤ p1
p2 ... pn + 1を示すが, それより実質的によい証明は1851年にロシアの数学者P. L.
Chebyshevの任意のnについてpn+1 ≤ 2pnであるという証明までなかった. この結果は元々1845年に推測であったが,
Bertrandの仮説 (Bertrand's hypothesis)として知られている. 証明は
Hardy and
Wright 1960の22.3節にある.
64
この問題は必要呼びが問題3.27に述べた
通常のメモ化に非常に関係あることを示している. あの問題では, 局所表を明確に構成するのに代入を使った. 必要呼びのストリーム最適化は値をストリームの以前に強制された部分に格納するので, 実質的にそういう表を自動的に構成する.