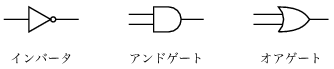
図3.24 ディジタル回路シミュレータの基本的機能
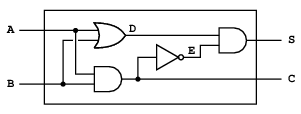
図3.25 半加算器の回路
回路の計算モデルは, 回路を構成する基本部品に対応するオブジェクトで組み立てられている. そこには
ディジタル信号(digital signals)を伝える
回線(wires)がある. ディジタル信号はある瞬間には二つの可能な値0と1の一つをとる. またいろいろな種類のディジタルな
機能箱(function boxes)があり, 入力信号を伝える回線と出力回線を繋ぐ. こういう箱は入力信号から計算した出力信号を出す. 出力信号は, 機能箱の型に対応した時間だけ
遅延する. 例えば
インバータ(inverter)は, 入力を反転する基本的な機能箱である. インバータへの入力信号が0に変ると, 一インバータ遅延の後, インバータは出力信号を1に変える. インバータへの入力信号が1に変ると, 一インバータ遅延の後, インバータは出力信号を0に変える. インバータを記号的に図3.24のように描く. やはり図3.24に示す
アンドゲート(and-gate)も二入力一出力の基本的機能箱である. 出力信号を入力信号の
論理積(logical and)の値に駆動する. つまり入力信号の両方が1になると, 一アンドゲート遅延の後, アンドゲートは出力信号を1に変える; そうでなければ, 出力は0である.
オアゲート(or-gate)も同様な二入力の基本的機能箱で, 出力信号を入力信号の
論理和(logical or)になるように駆動する. つまり, 少なくとも信号の一つが1になると, 出力は1になる; そうでなければ出力は0になる.

図3.24 ディジタル回路シミュレータの基本的機能

図3.25 半加算器の回路
基本機能を接続し, 更に複雑な機能が構成出来る. そのためには機能箱の出力を他の機能箱の入力に回線接続する. 例えば図3.25に示す 半加算器(half-adder)回路は, 一つのオアゲート, 二つのアンドゲートと一つのインバータで出来ている. それは二つの入力信号AとBをとり, 二つの出力信号SとCを出す. SはAとBの一方だけが1の時, 1となり, CはAとBの両方が1の時, 1になる. 図から分るように遅延が絡むので, 出力は別の時刻に生成される. ディジタル回路の設計の難しさの多くはこの事実から生じる.
これから学ぼうとするディジタル論理回路をモデル化するプログラムを作ろう. プログラムは信号を「保持」する回線をモデル化する計算オブジェクトを構成する. 機能箱は信号間の正しい関係を実現する手続きでモデル化する.
シミュレーションの基本要素の一つは, 回線を構成する手続き make-wireであろう. 六本の回線を次のように構成する:
(define a (make-wire)) (define b (make-wire)) (define c (make-wire)) (define d (make-wire)) (define e (make-wire)) (define s (make-wire))機能箱を一群の回線に接続するには, その箱の種類を構成する手続きを呼び出す. 構成子手続きへの引数は, その箱に接続する回線である. 例えばアンドゲート, オアゲートおよびインバータが構成出来るとして, 図3.25に示す半加算器が結線出来る:
(or-gate a b d) ok (and-gate a b c) ok (inverter c e) ok (and-gate d e s) ok
更にうまいことに, 半加算器に接続する四本の外部の回線に対し, この回路を構成する手続きhalf-adderを定義し, この演算に名前をつけることが出来る:
(define (half-adder a b s c)
(let ((d (make-wire)) (e (make-wire)))
(or-gate a b d)
(and-gate a b c)
(inverter c e)
(and-gate d e s)
'ok))
こう定義する利点は, half-adder自身を構成要素として使い, 更に複雑な回路が作り出せることだ. 例えば図3.26は二つの半加算器と一つのオアゲートを使って組み立てた
全加算器(full-adder)を示す.26
全加算器を次のように構成出来る:
(define (full-adder a b c-in sum c-out)
(let ((s (make-wire))
(c1 (make-wire))
(c2 (make-wire)))
(half-adder b c-in s c1)
(half-adder a s sum c2)
(or-gate c1 c2 c-out)
'ok))
full-adderを手続きとして定義したので, それを構成要素に使い, 更により複雑な回路を作り出すことが出来る. (例えば問題3.30参照)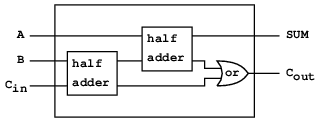
要するにわれわれのシミュレータは回路の言語を構成する道具を提供する. 1.1節でLispの勉強に利用した言語の一般的な視点を採用するなら, 基本的な機能箱は言語の組込み要素であり, 箱の結線は, 組合せの手段を用意することであり, 結線のパターンを手続きとして規定するのは, 抽象の手段として役立つ.
これらの手続きを使って基本的なディジタル論理関数が定義出来る. インバータを通して入力を出力に接続するには, add-action!を使い, 入力回線と, 入力回線の信号が値を変えた時に走るべき手続きを対応づける. 手続きは入力信号のlogical-notを計算し, 一inverter-delay後に出力信号を新しい値に設定する:
(define (inverter input output)
(define (invert-input)
(let ((new-value (logical-not (get-signal input))))
(after-delay inverter-delay
(lambda ()
(set-signal! output new-value)))))
(add-action! input invert-input)
'ok)
(define (logical-not s)
(cond ((= s 0) 1)
((= s 1) 0)
(else (error "Invalid signal" s))))
アンドゲートは多少複雑だ. アクション手続きはゲートへの入力のいずれかが変ったら走らなければならない. それは(logical-notに似た手続きを使い)入力回線の値のlogical-andを計算し, 一and-gate-delay後に出力回線に新しい値への変化が起きるように設定する.
(define (and-gate a1 a2 output)
(define (and-action-procedure)
(let ((new-value
(logical-and (get-signal a1) (get-signal a2))))
(after-delay and-gate-delay
(lambda ()
(set-signal! output new-value)))))
(add-action! a1 and-action-procedure)
(add-action! a2 and-action-procedure)
'ok)
(define (make-wire)
(let ((signal-value 0) (action-procedures '()))
(define (set-my-signal! new-value)
(if (not (= signal-value new-value))
(begin (set! signal-value new-value)
(call-each action-procedures))
'done))
(define (accept-action-procedure! proc)
(set! action-procedures (cons proc action-procedures))
(proc))
(define (dispatch m)
(cond ((eq? m 'get-signal) signal-value)
((eq? m 'set-signal!) set-my-signal!)
((eq? m 'add-action!) accept-action-procedure!)
(else (error "Unknown operation -- WIRE" m))))
dispatch))
局所手続きset-my-signal!は, 新しい信号の値が, その回線の信号を変えるかをテストする. そうであれば, 引数なしの手続きのリストの中の各項目を呼び出す次の手続きcall-eachを使い, アクション手続きのそれぞれを走らせる:
(define (call-each procedures)
(if (null? procedures)
'done
(begin
((car procedures))
(call-each (cdr procedures)))))
局所手続きaccept-action-procedure!は, 与えられた手続きを, 走らせるべき手続きのリストに追加し, 新しい手続きを一回走らせる. (問題3.31参照)
指定通りに設定された局所のdispatch手続きにより, 回線上の局所演算にアクセスする次の手続きを用意出来る: 27
(define (get-signal wire) (wire 'get-signal)) (define (set-signal! wire new-value) ((wire 'set-signal!) new-value)) (define (add-action! wire action-procedure) ((wire 'add-action!) action-procedure))
時と共に変る信号を持ち, 順次に装置に接続される回線は可変オブジェクトの代表である. われわれはそれを, 代入で修正する局所状態を持つ手続きとしてモデル化した. 新しい回線が作り出されると, 状態変数の新しい組が( make-wireのlet式で)割り当てられ, 環境に新しい状態変数を取り込んだ新しいdispatch手続きが構成され, 返される.
回線はそれに接続した多くの装置によって共有される. そこで, 一つの装置との相互作用で生じた変化は, その回線に継っているすべての装置に影響を及ぼす. 回線は接続が達成した時に貰ったアクション手続きを呼び出して, この変化をその近隣に通信する.
われわれの使う特定の次第書きをthe-agendaということにする. 手続きafter-delayは新しい要素をthe-agendaに追加する:
(define (after-delay delay action)
(add-to-agenda! (+ delay (current-time the-agenda))
action
the-agenda))
シミュレーションは, the-agendaを操作し, 次第書きにある各手続きを順次に実行する手続きpropagateが駆動する. 一般に, シミュレーションが進むにつれ, 新しい項目が次第書きに追加され, propagateは次第書きに項目がある限り, シミュレーションを継続する:
(define (propagate)
(if (empty-agenda? the-agenda)
'done
(let ((first-item (first-agenda-item the-agenda)))
(first-item)
(remove-first-agenda-item! the-agenda)
(propagate))))
(define (probe name wire)
(add-action! wire
(lambda ()
(newline)
(display name)
(display " ")
(display (current-time the-agenda))
(display " New-value = ")
(display (get-signal wire)))))
初めに次第書きを初期化し, 基本的な機能箱の遅延を指定する:
(define the-agenda (make-agenda)) (define inverter-delay 2) (define and-gate-delay 3) (define or-gate-delay 5)次に四本の回線を定義し, そのうち二本にプローブを置く:
(define input-1 (make-wire)) (define input-2 (make-wire)) (define sum (make-wire)) (define carry (make-wire)) (probe 'sum sum) sum 0 New-value = 0 (probe 'carry carry) carry 0 New-value = 0次に回線を(図3.25のように)半加算器に接続し, input-1の信号を1に設定し, シミュレーションを走らせる.
(half-adder input-1 input-2 sum carry) ok (set-signal! input-1 1) done (propagate) sum 8 New-value = 1 donesumの信号は時刻8に1に変った. 今はシミュレーションの開始から八単位時間のところにいる. ここでinput-2の信号を1に設定し, この値を伝播させることが出来る:
(set-signal! input-2 1) done (propagate) carry 11 New-value = 1 sum 16 New-value = 0 donecarryは時刻11に1に変り, sumは時刻16に0に変った.
(define (accept-action-procedure! proc) (set! action-procedures (cons proc action-procedures)))のように定義したら, システムの応答はどう違うかを述べよ.
次第書きは 時間区分(time segment)で出来ている. 各時間区分は数値(時刻)と, その時間区分の間に起きるように計画された手続きを保持する キュー(問題3.32参照)の対である.
(define (make-time-segment time queue) (cons time queue)) (define (segment-time s) (car s)) (define (segment-queue s) (cdr s))3.3.2節で述べたキュー演算を使い, 時間区分にあるキューを操作する.
次第書きそのものは時間区分の一次元の表である. これは3.3.3節に述べた表とは, 区分が時刻の増える順に格納されている点で違っている. その上 現在時刻(current time)(つまり処理された最後のアクションの時刻)を次第書きの先頭に格納する. 新しく構成した次第書きには, 時間区分が一個もなく, 現在時刻は0である:28
(define (make-agenda) (list 0)) (define (current-time agenda) (car agenda)) (define (set-current-time! agenda time) (set-car! agenda time)) (define (segments agenda) (cdr agenda)) (define (set-segments! agenda segments) (set-cdr! agenda segments)) (define (first-segment agenda) (car (segments agenda))) (define (rest-segments agenda) (cdr (segments agenda)))
時間区分が一つもなければ, 次第書きは空である:
(define (empty-agenda? agenda) (null? (segments agenda)))
アクションを次第書きに追加するには, まず次第書きが空かを見る. そうであれば, そのアクションのために時間区分を作り出し, それを次第書きに設定する. そうでなければ, 各区分の時刻を調べながら, 次第書きを走査する. 指定の時刻の区分を見つけたら, アクションを対応するキューに追加する. 指定の時刻より遅い時刻に達したら, 次第書きのその直前に, 新しい時間区分を挿入する. 次第書きの最後に達したら, 最後に新しい時間区分を作り出さなければならない.
(define (add-to-agenda! time action agenda)
(define (belongs-before? segments)
(or (null? segments)
(< time (segment-time (car segments)))))
(define (make-new-time-segment time action)
(let ((q (make-queue)))
(insert-queue! q action)
(make-time-segment time q)))
(define (add-to-segments! segments)
(if (= (segment-time (car segments)) time)
(insert-queue! (segment-queue (car segments))
action)
(let ((rest (cdr segments)))
(if (belongs-before? rest)
(set-cdr!
segments
(cons (make-new-time-segment time action)
(cdr segments)))
(add-to-segments! rest)))))
(let ((segments (segments agenda)))
(if (belongs-before? segments)
(set-segments!
agenda
(cons (make-new-time-segment time action)
segments))
(add-to-segments! segments))))
次第書きから先頭の項目を除去する手続きは, 最初の時間区分のキューの先頭の項目を削除する. この削除で, 時間区分が空になれば, それを区分のリストから除去する:29
(define (remove-first-agenda-item! agenda)
(let ((q (segment-queue (first-segment agenda))))
(delete-queue! q)
(if (empty-queue? q)
(set-segments! agenda (rest-segments agenda)))))
次第書きの最初の項目は, 最初の時間区分のキューの先頭で見つかる. 項目を取り出した時には, 現在時刻も更新する:30
(define (first-agenda-item agenda)
(if (empty-agenda? agenda)
(error "Agenda is empty -- FIRST-AGENDA-ITEM")
(let ((first-seg (first-segment agenda)))
(set-current-time! agenda (segment-time first-seg))
(front-queue (segment-queue first-seg)))))
26
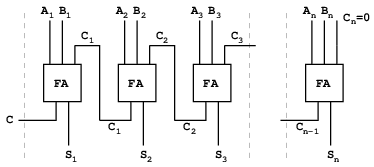
全加算器は二つの二進数を足すのに使う基本的な回路素子である. AとBは足すべき二つの数の対応する位置のビットで, Cinは一桁右の加算からの繰上りビットである. 回路は対応する位置の和のビットであるSUMと, 左へ伝播する繰上りビットのCoutを生成する.
27
これらの手続きは, オブジェクトの局所手続きにアクセスするのに, 通常の手続きの構文を使うための, 構文シュガーである. こういう単純な方法で「手続き」と「データ」の役割が交換出来るのは驚きである. 例えば(wire 'get-signal)と書けば, wireは, メッセージget-signal
を入力として呼び出された手続きと思ってしまう. また(get-signal wire)の書き方はwireは手続きget-signalへの入力になるオブジェクトだと思わせる. 本当のところは, 手続きをオブジェクトとして扱うことの出来る言語では, 「手続き」と「データ」の間に基本的な違いはなく, 構文シュガーを選んで,
選んだ流儀のプログラムを書くことが出来る.
28
次第書きは, 3.3.3節の表のような
頭つきリストであるが, リストには時刻の頭がついているので, (表で使った*table*記号のような)余計なダミーの頭は必要ない.
29
この手続きのif式には⟨alternative⟩がないことに注意しよう.
こういう「隻腕if文」は, 二つの式から選択するのではなく, 何かをするかしないかを決めるのに使う. 述語が偽で, ⟨alternative⟩がない時は,
if式は特には指定しない値を返す.
30
このようにして現在時刻は最も最近に処理したアクションの時刻になっている. この時刻を次第書きの先頭に格納するので, 対応する時間区分が削除されても, そこにあることが保証される.