まずそれぞれの値が一つのキーで格納される一次元の表を考える. 表をレコードのリストとして実装し, 各レコードはキーと対応づけられた値からなる対として実装する. レコードは, carが順次のレコードを指している対で糊づけされたリストとなる. 糊づけした対は表の 背骨(backbone)という. 新しいレコードを表に追加する時に, 変更する場所が必要なので, 表を 頭つきリスト(headed list)にする. 頭つきリストには先頭に特別な背骨の対があり, ダミーのレコード---今の場合は任意に選んだ記号 *table*---を持っている. 図3.22は表
a: 1 b: 2 c: 3の箱とポインタ図を示す.
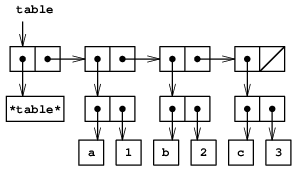
表から情報を取り出すには, 引数としてキーをとり, 対応づけられた値を返す(または, そのキーで格納した値がなければ, 偽となる.)lookup手続きを使う. lookup手続きは, 引数としてキーとレコードのリストをとるassoc演算を使って定義する. assocはダミーのレコードを見ないことに注意しよう. assocはcarに与えられたキーを持つレコードを返す.~24 lookupはassocが返した結果のレコードが偽でないことを見, レコードの値(cdr)を返す.
(define (lookup key table)
(let ((record (assoc key (cdr table))))
(if record
(cdr record)
false)))
(define (assoc key records)
(cond ((null? records) false)
((equal? key (caar records)) (car records))
(else (assoc key (cdr records)))))
指定したキーで値を表に挿入するには, assocを使い, 表に既にこのレコードが存在するかを見る. なければ, キーと値をconsして新しいレコードを作り, これを表のレコードのリストの先頭にあるダミーのレコードの後に挿入する. このキーのレコードが既に存在していれば, そのレコードの cdrを, 指示した新しい値に設定する. 表の先頭は新しいレコードを挿入するために修正する固定の場所を用意する.25
(define (insert! key value table)
(let ((record (assoc key (cdr table))))
(if record
(set-cdr! record value)
(set-cdr! table
(cons (cons key value) (cdr table)))))
'ok)
新しい表を構成するには, 記号*table*を含むリストを作り出すだけでよい.
(define (make-table) (list '*table*))
math:
+: 43
-: 45
*: 42
letters:
a: 97
b: 98
の箱とポインタ図を示す. (下位の表を識別するキーがその目的を果すので,
下位の表には特別の頭部の記号は必要ない.)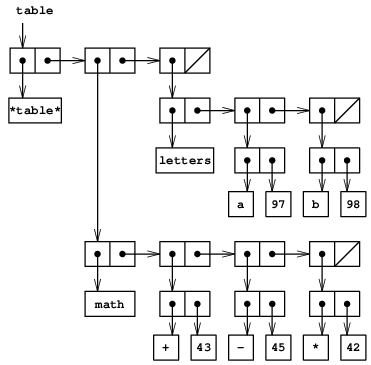
項目を探すには, 第一のキーを使い正しい下位の表を見つける. 次に第二のキーを使い,下位の表からレコードを見つける.
(define (lookup key-1 key-2 table)
(let ((subtable (assoc key-1 (cdr table))))
(if subtable
(let ((record (assoc key-2 (cdr subtable))))
(if record
(cdr record)
false))
false)))
一対のキーで新しい項目を挿入するにはassocを使い, 第一のキーで格納した下位の表があるかを見る. なければ, 唯一のレコード(key-2, value)を含む新しい下位の表を作り, 第一のキーで表に挿入する. 下位の表が既に存在すれば, 上に述べた一次元の挿入法を使い, この下位の表に新しいレコードを挿入する:
(define (insert! key-1 key-2 value table)
(let ((subtable (assoc key-1 (cdr table))))
(if subtable
(let ((record (assoc key-2 (cdr subtable))))
(if record
(set-cdr! record value)
(set-cdr! subtable
(cons (cons key-2 value)
(cdr subtable)))))
(set-cdr! table
(cons (list key-1
(cons key-2 value))
(cdr table)))))
'ok)
(define (make-table)
(let ((local-table (list '*table*)))
(define (lookup key-1 key-2)
(let ((subtable (assoc key-1 (cdr local-table))))
(if subtable
(let ((record (assoc key-2 (cdr subtable))))
(if record
(cdr record)
false))
false)))
(define (insert! key-1 key-2 value)
(let ((subtable (assoc key-1 (cdr local-table))))
(if subtable
(let ((record (assoc key-2 (cdr subtable))))
(if record
(set-cdr! record value)
(set-cdr! subtable
(cons (cons key-2 value)
(cdr subtable)))))
(set-cdr! local-table
(cons (list key-1
(cons key-2 value))
(cdr local-table)))))
'ok)
(define (dispatch m)
(cond ((eq? m 'lookup-proc) lookup)
((eq? m 'insert-proc!) insert!)
(else (error "Unknown operation -- TABLE" m))))
dispatch))
make-tableを使うと, 2.4.3節のデータ主導プログラミングで使ったgetとputの演算を次のように実装出来る:
(define operation-table (make-table)) (define get (operation-table 'lookup-proc)) (define put (operation-table 'insert-proc!))getは引数として二つのキーを, putは引数として二つのキーと一つの値をとる. どちらの演算も, make-tableの呼出しが作り出したオブジェクトにカプセル化された, 同じ局所表にアクセスする.
(define (fib n)
(cond ((= n 0) 0)
((= n 1) 1)
(else (+ (fib (- n 1))
(fib (- n 2))))))
同じ手続きのメモ化版は
(define memo-fib
(memoize (lambda (n)
(cond ((= n 0) 0)
((= n 1) 1)
(else (+ (memo-fib (- n 1))
(memo-fib (- n 2))))))))
で, そのメモ化手続きは
(define (memoize f)
(let ((table (make-table)))
(lambda (x)
(let ((previously-computed-result (lookup x table)))
(or previously-computed-result
(let ((result (f x)))
(insert! x result table)
result))))))
で定義する. (memo-fib 3)の計算を解析する環境の図を描け.
memo-fibがn番目のFibonacci数をnに比例したステップ数で計算出来る理由を説明せよ. この方式はmemo-fibを単に(memoize fib)と定義してもやはり働くだろうか.
24
assocはequal?を使うので, キーが記号, 数値,リスト構造のいずれでも判別する.
25
背骨の最初の対は, 表「自身」を表現するオブジェクトである; つまり表へのポインタはこの対へのポインタである. この背骨の対は, 常に表の先頭である. 表をこのように配置しないと,
insert!は新しいレコードを追加すると, 表の先頭としての新しい値を返さなければならない.