[ 目次, 前節, 次節, 索引 ]

   キュー(queue)は項目を一方の端 (キューの後尾(rear)という)から挿入し, 他方の端 (先頭(front))から削除する並びである. 図3.18は最初は空のキューに, 項目aとbを挿入したものである. 次にaを削除, cとdを挿入, bを削除する. 項目は常に挿入した順に削除するので, キューは FIFO(first in first out)バッファということがある.



図3.18 キュー演算

  データ抽象を使い, キューを次の演算で定義したと考える:

• 構成子:
(make-queue)
空のキュー(項目の一つもないキュー)を返す.

• 二つの選択子:
(empty-queue? ⟨queue⟩)
キューが空であることをテストする.

(front-queue ⟨queue⟩)
キューの先頭のオブジェクトを返す. キューが空ならエラーとする. キューは修正しない.

• 二つの変更子:
(insert-queue! ⟨queue⟩  ⟨item⟩)
キューの後尾に項目を挿入し, 修正したキューを値として返す.

(delete-queue! ⟨queue⟩)
キューの先頭の項目を削除し, 修正したキューを値として返す. 削除の前にキューが空ならエラーとする.

   キューは項目の並びだから, 当然これを通常のリストとして表現出来る; キューの先頭はリストのcarである. キューに項目を挿入するには, 新しい項目をリストの最後に挿入連結することになる. キューからの項目の削除は, 単にリストのcdrをとることだ. しかしこの表現は, 項目を挿入するのに, リストを最後まで走査しなければならず, 非効率である. リストを走査するための唯一の手段はcdr演算の繰返しだから, n項目のリストでは, 走査にΘ(n)のステップが必要である. リスト表現の単純な修正が, この欠点を克服し, キュー演算をΘ(1)ステップを必要とするように, 実装出来る; つまり必要なステップ数は, キューの長さと無関係にある.

   リスト表現の困難は, リストの最後を見つけるための走査が必要なことである. 走査が必要な理由は, リストを対の鎖で表現する標準的方法では, リストの最初へのポインタは, 容易に得られるが, 最後へアクセスするポインタは容易には得られないことだ. この不利を避ける修正は, キューをリストで表現し, 同時にリストの最後の対を指示するポインタを追加することである. 項目を挿入しようとする時は, 後尾ポインタを見ればよく, リストの走査は避けられる.

   そこでキューはそれぞれ通常のリストの最初と最後の対を指示する一対のポインタfront-ptrとrear-ptrで表現する. キューを一まとまりのオブジェクトにしたいので, consを使って二つのポインタを組み合せる. つまりキュー自身は二つのポインタのconsとなる. 図3.19にこの表現を示す.



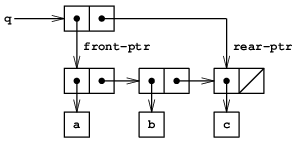
図3.19 先頭と後尾のポインタつきリストによるキューの実装

   キュー演算を次の手続きを使って定義する. これにより, キューと先頭と後尾のポインタを選択し, 修正出来る:

(define (front-ptr queue) (car queue))


(define (rear-ptr queue) (cdr queue))


(define (set-front-ptr! queue item) (set-car! queue item))


(define (set-rear-ptr! queue item) (set-cdr! queue item))

   これで実際のキュー演算が実装出来る. 先頭のポインタが空リストなら, キューは空だと考える:

(define (empty-queue? queue) (null? (front-ptr queue)))

(define (make-queue) (cons '() '()))

(define (front-queue queue)
  (if (empty-queue? queue)
      (error "FRONT called with an empty queue" queue)
      (car (front-ptr queue))))

   キューに項目を挿入するには, その結果が図3.20に示すものになる方法をとる. まずcarが挿入すべき項目で, cdrが空リストである新しい対を作り出す. キューが初めから空なら, キューの先頭と後尾のポインタをこの対へ設定する. そうれなければ, キューの最後の対を, この新しい対を指すように修正し, また後尾ポインタを新しい対へ設定する.



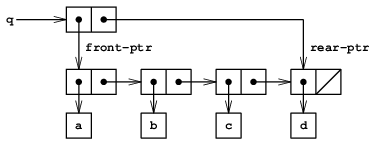
図3.20 図3.19のキューに(insert-queue! q 'd)を使った結果

(define (insert-queue! queue item)
  (let ((new-pair (cons item '())))
    (cond ((empty-queue? queue)
           (set-front-ptr! queue new-pair)
           (set-rear-ptr! queue new-pair)
           queue)
          (else
           (set-cdr! (rear-ptr queue) new-pair)
           (set-rear-ptr! queue new-pair)
           queue)))) 

   キューの先頭の項目を削除するには, 先頭のポインタを, 先頭の項の cdrポインタを辿ると見つかるキューの二番目の項目を指すように変更するだけである(図3.21参照):22



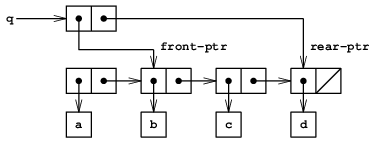
図3.21 図3.20のキューに(delete-queue! q)を使った結果

(define (delete-queue! queue)
  (cond ((empty-queue? queue)
         (error "DELETE! called with an empty queue" queue))
        (else
         (set-front-ptr! queue (cdr (front-ptr queue)))
         queue))) 

(define q1 (make-queue))

(insert-queue! q1 'a)
((a) a)

(insert-queue! q1 'b)
((a b) b)

(delete-queue! q1)
((b) b)

(delete-queue! q1)
(() b)

(define (make-queue)
  (let ((front-ptr ... )
        (rear-ptr ... ))
    ⟨内部手続きの定義⟩
    (define (dispatch m) ...)
    dispatch))

22 先頭の項目がキューの最後の項目なら, 先頭のポインタは削除の後, 空リストになり, キューは空になる; 後尾ポインタは依然として削除した項目を指してはいるが, empty-queue?は先頭のポインタだけ見ているので, 更新を気にする必要はない.

23 解釈系に循環を含む構造を印字させないよう注意せよ. (問題3.13参照)

[ 目次, 前節, 次節, 索引 ]