[ 目次, 前節, 次節, 索引 ]

   対の基本変更子はset-car!とset-cdr!である. set-car!は二つの引数をとり, 第一の引数は対でなければならない. それは, car ポインタをset-car!の第二引数へのポインタで取り替え, 対を修正する. 16

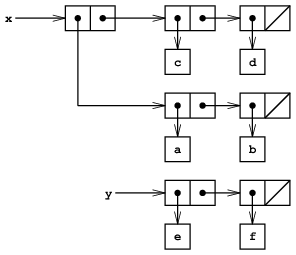
   例として図3.12に示すように, xがリスト((a b) c d), y がリスト(e f)に束縛されているとする. 式(set-car! x y)の評価はxが束縛されている対を, そのcarをyの値で取り替えて, 修正する. 演算の結果を図3.13に示す. xの構造は修正され, 今は((e f) c d)と印字されるであろう. 取り替えられたポインタが指していたリスト(a b)を表現していたいくつかの対は, 今は元の構造から切り離されている.17

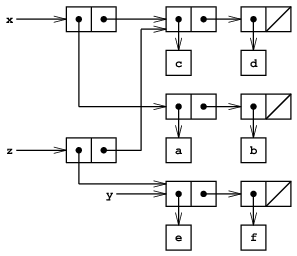
   図3.13と, xとyは図3.12の元のリストに束縛されているとし, (define z (cons y (cdr x)))を実行した結果の図3.14を比べよう. 変数zはcons演算で作り出した新しい対に束縛されている; x が束縛されているリストは変らない.

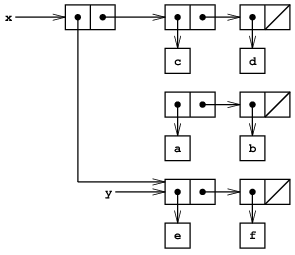
   set-cdr!は演算set-car!に似ている. 違いは対のcarポインタでなく, cdrポインタを取り替える. 図3.12のリストに (set-cdr! x y)を実行した効果を図3.15に示す. ここではxのcdrポインタが(e f)へのポインタに取り替っている. 又リスト(c d)はxのcdrであったが, 今は構造から切り離されている.

   consは新しい対を作り出して新しいリスト構造を作るが, set-car!とset-cdr!は現存の対を修正する. 実際consは二つの変更子と, 既存のリスト構造の部分にはない新しい対を返す手続きget-new-pairを使って実装出来る. 新しい対を貰い, そのcarとcdrのポインタを, 指定するオブジェクトに設定し, 新しい対をconsの結果として返す.18

(define (cons x y)
  (let ((new (get-new-pair)))
    (set-car! new x)
    (set-cdr! new y)
    new))

(define (append x y)
  (if (null? x)
      y
      (cons (car x) (append (cdr x) y))))

(define (append! x y)
  (set-cdr! (last-pair x) y)
  x)

(define (last-pair x)
  (if (null? (cdr x))
      x
      (last-pair (cdr x))))

(define x (list 'a 'b))

(define y (list 'c 'd))

(define z (append x y))

z
(a b c d)

(cdr x)
⟨応答⟩

(define w (append! x y))

w
(a b c d)

(cdr x)
⟨応答⟩

(define (make-cycle x)
  (set-cdr! (last-pair x) x)
  x)

(define z (make-cycle (list 'a 'b 'c)))

(define (mystery x)
  (define (loop x y)
    (if (null? x)
        y
        (let ((temp (cdr x)))
          (set-cdr! x y)
          (loop temp x))))
  (loop x '()))

共有と同一

(define x (list 'a 'b))
(define z1 (cons x x))

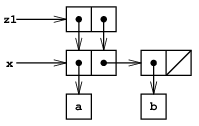
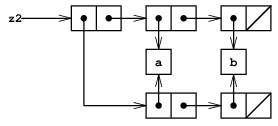
   図3.16に対し, 図3.17は

(define z2 (cons (list 'a 'b) (list 'a 'b)))

   リストとして考えると, z1とz2は「同じ」リスト((a b) a b)を表現する. 一般にリストをcons, carおよびcdrだけを使って演算すると, 共有は検出不能である. しかしリスト構造に変更を認めると, 共有は重要になる. 共有の作る違いの例として, それを作用させる構造のcarを修正する次の手続き

(define (set-to-wow! x)
  (set-car! (car x) 'wow)
  x)

z1
((a b) a b)

(set-to-wow! z1)
((wow b) wow b)

z2
((a b) a b)

(set-to-wow! z2)
((wow b) a b)

   リスト構造での共有を検出する一つの方法は, 2.3.1節で二つの記号が等価かどうかをテストする方法として説明した述語eq?を使うことである. 更に一般には, (eq? x y)はxとyは同じオブジェクトであるか(つまりxとyはポインタとして同じか)をテストする. そこで図3.16と3.17で定義したz1とz2では(eq? (car z1) (cdr z1)) は真であり, (eq? (car z2) (cdr z2))は偽である.

   後の節で見るように対により表現出来るデータ構造のレパートリを大いに拡張するのに, 共有が利用出来る. 一方, 構造の修正は, たまたま修正した部分を共有していた他の構造にも影響するので, 危険でもある. 変更演算子set-car!とset-cdr!は注意して使うべきである: データオブジェクトがどう共有されているかの十分な理解がないと, 変更は予期せぬ結果をもたらす.20

問題 3.15

上の構造z1とz2へのset-to-wow!の効果を説明する箱とポインタ図を描け.

問題 3.16

Ben Bitdiddleはリスト構造中の対の個数を数える手続きを書こうと決心した. 「簡単だ」と考えた. 「任意の構造の対の個数はcarにある個数足すcdrにある個数足す今いる対の1である.」そこでBenは次の手続きを書いた:

(define (count-pairs x)
  (if (not (pair? x))
      0
      (+ (count-pairs (car x))
         (count-pairs (cdr x))
         1)))

変更は単なる代入

(define (cons x y)
  (define (dispatch m)
    (cond ((eq? m 'car) x)
          ((eq? m 'cdr) y)
          (else (error "Undefined operation -- CONS" m))))
  dispatch)


(define (car z) (z 'car))


(define (cdr z) (z 'cdr))

(define (cons x y)
  (define (set-x! v) (set! x v))
  (define (set-y! v) (set! y v))
  (define (dispatch m)
    (cond ((eq? m 'car) x)
          ((eq? m 'cdr) y)
          ((eq? m 'set-car!) set-x!)
          ((eq? m 'set-cdr!) set-y!)
          (else (error "Undefined operation -- CONS" m))))
  dispatch)


(define (car z) (z 'car))


(define (cdr z) (z 'cdr))


(define (set-car! z new-value)
  ((z 'set-car!) new-value)
  z)


(define (set-cdr! z new-value)
  ((z 'set-cdr!) new-value)
  z)

   可変データの振舞いを説明するには, 理論的には代入だけが必要だ. われわれの言語にset!を認めると, 代入だけではなく, 一般の可変データの問題も浮び上ってくる.21

問題 3.20

上の対の手続き実装を使って一連の式

(define x (cons 1 2))
(define z (cons x x))
(set-car! (cdr z) 17)

(car x)
17

16 set-car!とset-cdr!は実装に依存した値を返す. set!と同様に, これらは効果のためにだけ使う.

17 このことから, リストの変更演算は, アクセス可能な構造の部分ではない「ごみ」を作り出すことがあるのを知る. 5.3.2節のLispの記憶管理システムには, 不要になった対の使っているスペースを探し再生する ごみ集め(garbage collection)があることを見る.

18 get-new-pairはLispの実装に必要な記憶管理の一部として実装しなければならない演算の一つである. 5.3.1節でこれを議論する.

19 二つの対が別なのはconsは呼出し毎に新しい対を作るからである. 記号は共有する; Schemeではどの名前でも 記号は唯一である. Schemeには記号を変化させる手段はなく, この共有は検出不能である. 共有の故に単にポインタの等価を調べるeq?を使って記号が比べられる.

20 可変データオブジェクトの共有に関する難しさは, 3.1.3節で持ち上った「同一」と「変更」の基盤の論点を思い起す. そこでは言語に変更を認めると合成オブジェクトは, それが作られた部品とは何か違う「同一性」を持たなければならないと述べた. Lispではこの「同一性」はeq?でテスト出来る等価性(つまりポインタの等価性)と考える. 大抵のLispの実装ではポインタは本質的に記憶装置のアドレスだから, オブジェクトの同一性の定義という「問題を解決する」のに, データオブジェクト「自身」は, 計算機の記憶場所の特別な部分に記憶された情報であると規定すればよい. これは単純なLisp システムでは十分だが, 計算モデルの「同じ」ことの論点を解決する一般的方法にはなりえない.

21 他方, 実装の観点から, 代入はそれ自身可変データ構造である環境の修正を必要とする. つまり代入と変更は同能力なもので, 一方は他方を使って実装出来る.

[ 目次, 前節, 次節, 索引 ]