[ 目次, 前節, 次節, 索引 ]

   本節では関係そのものを使って仕事が出来るような言語の設計を眺めよう. この言語の基本要素は, 量の間にはある関係が成り立つことを述べる 基本制約(primitive constraints)である. 例えば(adder a b c) は, 量a, bおよびcは方程式a + b = cで関係づけられていることを規定し, (multiplier x y z)は制約xy = zを表し, (constant 3.14 x) はxの値は3.14でなければならないといっている.

   われわれの言語は, 基本制約を組み合せ, 更に複雑な関係を表す手段を提供する. 制約は 制約ネットワーク(constraint networks)を構成して組み合せる. 制約は コネクタ(connectors)で接続する. コネクタは一つか複数の制約に関る値を「保持する」オブジェクトである. 例えばカ氏[Fahrenheit]の温度Fとセ氏[Celsius]の温度Cの間には

9C = 5(F - 32)

の関係があることを知っている. こういう関係は, 基本加算器, 乗算器と定数の制約から出来ているネットワークと考えることが出来る(図3.28). この図の左には, m1, m2およびpでラベルした三つの端子を持つ乗算器があり, それらは乗算器を次のようにネットワークの他の部分へ接続している: m1端子は, セ氏の温度を保持するコネクタCに結合されている. m2端子はコネクタwに結合され, それはまた9を保持する定数箱に結合されている. 乗算箱がm1とm2の積だと制約を与えているp端子は, もう一つの乗算箱のp端子に結合され, そちらのm2は定数5に, m1は和の一つの項へ繋いである.



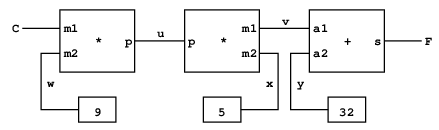
図3.28 制約ネットワークで表した関係9C = 5(F - 32)

   こういうネットワークの計算は次のように進行する: (利用者または, それに結合している制約箱により)コネクタに値が与えられると, (自分を起した制約以外の)関係あるすべての制約を起し, 値を持ったことを知らせる. 起された各制約箱は, コネクタを見回し, コネクタの値を決めるのに十分な情報があるかを見る. そうであれば, 箱はコネクタを設定し, そのコネクタは, 関係する制約をすべて起す. これを繰り返す. 例えばセ氏とカ氏の間の変換では, w, xおよびyは, それぞれ定数箱9, 5および32により直ちに設定される. これらのコネクタは乗算器と加算器を起すが, それらは進むには十分な情報がないことを知る. 利用者(またはネットワークの他の部分)がCをある値(例えば25)に設定すると, 左端の乗算器は起され, uを25 ... 9 = 225に設定する. するとuは二番目の乗算器を起すが, それはvを45に設定し, vは加算器を起し, それはFを77に設定する.

制約システムの使い方

(define C (make-connector))
(define F (make-connector))
(celsius-fahrenheit-converter C F)
ok

(define (celsius-fahrenheit-converter c f)
  (let ((u (make-connector))
        (v (make-connector))
        (w (make-connector))
        (x (make-connector))
        (y (make-connector)))
    (multiplier c w u)
    (multiplier v x u)
    (adder v y f)
    (constant 9 w)
    (constant 5 x)
    (constant 32 y)
    'ok))

   ネットワークの動作を見るため, 3.3.4節で回線を監視するのに使ったのと似たprobe手続きを使い, コネクタCとFにプローブを置く. コネクタにプローブを置くと, コネクタに値が与えられる度にメッセージが印字される:

(probe "Celsius temp" C)
(probe "Fahrenheit temp" F)

(set-value! C 25 'user)
Probe: Celsius temp = 25
Probe: Fahrenheit temp = 77
done

   ところでFを新しい値, 例えば212に設定して見ることが出来る.

(set-value! F 212 'user)
Error! Contradiction (77 212)

(forget-value! C 'user)
Probe: Celsius temp = ?
Probe: Fahrenheit temp = ?
done

   今やFには値がないので, それを212に設定するのは自由だ:

(set-value! F 212 'user)
Probe: Fahrenheit temp = 212
Probe: Celsius temp = 100
done

制約システムの実装

   コネクタの基本演算は次の通り:

• (has-value? ⟨connector⟩)
コネクタが値を持つかどうかを告げる.

• (get-value ⟨connector⟩)
コネクタの現在の値を返す.

• (set-value! ⟨connector⟩  ⟨new-value⟩  ⟨informant⟩)
通知者はコネクタに新しい値を設定するよう要求していることを示す.

• (forget-value! ⟨connector⟩  ⟨retractor⟩)
撤回者がその値を忘れるように要求していることをコネクタに告げる.

• (connect ⟨connector⟩  ⟨new-constraint⟩)
コネクタに新しい制約に関るよう告げる.

   コネクタは, コネクタが値を持つことを制約に告げる手続き inform-about-valueと, コネクタは値を持たないと制約に告げるinform-about-no-valueを使い, 制約と通信する.

   adderはa1とa2の被加算コネクタとsumコネクタの間に加算制約を構成する. 加算器は局所状態(次の手続きme)を持つ手続きとして実装される:

(define (adder a1 a2 sum)
  (define (process-new-value)
    (cond ((and (has-value? a1) (has-value? a2))
           (set-value! sum
                       (+ (get-value a1) (get-value a2))
                       me))
          ((and (has-value? a1) (has-value? sum))
           (set-value! a2
                       (- (get-value sum) (get-value a1))
                       me))
          ((and (has-value? a2) (has-value? sum))
           (set-value! a1
                       (- (get-value sum) (get-value a2))
                       me))))
  (define (process-forget-value)
    (forget-value! sum me)
    (forget-value! a1 me)
    (forget-value! a2 me)
    (process-new-value))
  (define (me request)
    (cond ((eq? request 'I-have-a-value)  
           (process-new-value))
          ((eq? request 'I-lost-my-value) 
           (process-forget-value))
          (else 
           (error "Unknown request -- ADDER" request))))
  (connect a1 me)
  (connect a2 me)
  (connect sum me)
  me)

(define (inform-about-value constraint)
  (constraint 'I-have-a-value))


(define (inform-about-no-value constraint)
  (constraint 'I-lost-my-value))

   乗算器も加算器に非常に似ている. 因子のいずれかが0なら, もう一方の因子が分らなくてもproductを0に設定する.

(define (multiplier m1 m2 product)
  (define (process-new-value)
    (cond ((or (and (has-value? m1) (= (get-value m1) 0))
               (and (has-value? m2) (= (get-value m2) 0)))
           (set-value! product 0 me))
          ((and (has-value? m1) (has-value? m2))
           (set-value! product
                       (* (get-value m1) (get-value m2))
                       me))
          ((and (has-value? product) (has-value? m1))
           (set-value! m2
                       (/ (get-value product) (get-value m1))
                       me))
          ((and (has-value? product) (has-value? m2))
           (set-value! m1
                       (/ (get-value product) (get-value m2))
                       me))))
  (define (process-forget-value)
    (forget-value! product me)
    (forget-value! m1 me)
    (forget-value! m2 me)
    (process-new-value))
  (define (me request)
    (cond ((eq? request 'I-have-a-value)
           (process-new-value))
          ((eq? request 'I-lost-my-value)
           (process-forget-value))
          (else
           (error "Unknown request -- MULTIPLIER" request))))
  (connect m1 me)
  (connect m2 me)
  (connect product me)
  me)

(define (constant value connector)
  (define (me request)
    (error "Unknown request -- CONSTANT" request))
  (connect connector me)
  (set-value! connector value me)
  me)

(define (probe name connector)
  (define (print-probe value)
    (newline)
    (display "Probe: ")
    (display name)
    (display " = ")
    (display value))
  (define (process-new-value)
    (print-probe (get-value connector)))
  (define (process-forget-value)
    (print-probe "?"))
  (define (me request)
    (cond ((eq? request 'I-have-a-value)
           (process-new-value))
          ((eq? request 'I-lost-my-value)
           (process-forget-value))
          (else
           (error "Unknown request -- PROBE" request))))
  (connect connector me)
  me)

コネクタの表現

(define (make-connector)
  (let ((value false) (informant false) (constraints '()))
    (define (set-my-value newval setter)
      (cond ((not (has-value? me))
             (set! value newval)
             (set! informant setter)
             (for-each-except setter
                              inform-about-value
                              constraints))
            ((not (= value newval))
             (error "Contradiction" (list value newval)))
            (else 'ignored)))
    (define (forget-my-value retractor)
      (if (eq? retractor informant)
          (begin (set! informant false)
                 (for-each-except retractor
                                  inform-about-no-value
                                  constraints))
          'ignored))
    (define (connect new-constraint)
      (if (not (memq new-constraint constraints))
          (set! constraints 
                (cons new-constraint constraints)))
      (if (has-value? me)
          (inform-about-value new-constraint))
      'done)
    (define (me request)
      (cond ((eq? request 'has-value?)
             (if informant true false))
            ((eq? request 'value) value)
            ((eq? request 'set-value!) set-my-value)
            ((eq? request 'forget) forget-my-value)
            ((eq? request 'connect) connect)
            (else (error "Unknown operation -- CONNECTOR"
                         request))))
    me))

   コネクタの局所手続きset-my-valueはコネクタの値を設定する要求がある時に呼び出される. 現在コネクタが値を持っていなければ, その値を設定し, informantとしてその値の設定を要求した制約を記憶する. 32 次にコネクタは, 値の設定を要求した制約を除き, すべての関りのある制約に知らせる. これは 指示した手続きを, 与えられたものを除き, リストのすべての項目に作用させる, 次の反復子を使って達成する:

(define (for-each-except exception procedure list)
  (define (loop items)
    (cond ((null? items) 'done)
          ((eq? (car items) exception) (loop (cdr items)))
          (else (procedure (car items))
                (loop (cdr items)))))
  (loop list))

   コネクタが値を忘れるよう頼まれると, 局所手続きforget-my-valueを呼び出す. この手続きはまず要求が確かに値を元々設定したのと同じオブジェクトから来ているかを調べる. そうであればコネクタは関りある制約に, 値のなくなったことを知らせる.

   局所手続きconnectは, リストにまだ存在していなければ指示された新しい制約を制約のリストに追加する. 次にコネクタが値を持てば, 新しい制約にこの事実を知らせる.

   コネクタの手続きmeは, 他の内部手続きへの振分けとして役立ち, またコネクタをオブジェクトとして表現する. 次の手続きは振分けの構文インターフェースを提供する:

(define (has-value? connector)
  (connector 'has-value?))


(define (get-value connector)
  (connector 'value))


(define (set-value! connector new-value informant)
  ((connector 'set-value!) new-value informant))


(define (forget-value! connector retractor)
  ((connector 'forget) retractor))


(define (connect connector new-constraint)
  ((connector 'connect) new-constraint))

(define (squarer a b)
  (multiplier a a b))

(define (squarer a b)
  (define (process-new-value)
    (if (has-value? b)
        (if (< (get-value b) 0)
            (error "square less than 0 -- SQUARER" (get-value b))
            ⟨代替部1⟩)
        ⟨代替部2⟩))
  (define (process-forget-value) ⟨本体1⟩)
  (define (me request) ⟨本体2⟩)
  ⟨定義の残り⟩
  me)

(define a (make-connector))
(define b (make-connector))
(set-value! a 10 'user)

(for-each-except setter inform-about-value constraints)

(define (celsius-fahrenheit-converter x)
  (c+ (c* (c/ (cv 9) (cv 5))
          x)
      (cv 32)))

(define C (make-connector))
(define F (celsius-fahrenheit-converter C))

(define (c+ x y)
  (let ((z (make-connector)))
    (adder x y z)
    z))

31 制約拡散は Ivan Sutherland(1963)の信じ難いほどの先見性を持った SKETCHPADに初めて現れた. Smalltalk言語に基づいた美しい制約拡散システムは Xerox Palo Alto研究所で Alan Borning(1977)が開発した. Sussman, Stallmanと Steeleは制約拡散を電気回路解析に応用した(Sussman and Stallman 1975; Sussman and Steele 1980). TK!Solver (Konopasek and Jayaraman 1984)は制約に基づいた強力なモデリング環境である.

32 setterは制約でないかも知れない. 温度の例では, userをsetterに使った.

33 式主導の形式は計算の中間の式に名前をつける必要がないから便利である. 多くの言語が合成データを扱おうとすると煩わしくなるように, 制約言語の初めの形式化も煩わしい. 例えば, 変数がベクタを表すとして, 積(a + b) ... (c + d)を計算する時, 指示したベクタの値を設定するが, 値としてはベクタを返さない手続きを使い, 「命令的流儀で」仕事をすることが出来る:

(v-sum a b temp1)
(v-sum c d temp2)
(v-proc temp1 temp2 answer)

一方値としてベクタを返す手続きを使って式を扱い, temp1やtemp2といちいちいわないで済むこともある.

(define answer (v-prod (v-sum a b) (v-sum c d)))

Lispは手続きの値として合成オブジェクトを返すことが出来るので, 命令形流儀の制約言語をこの問題のような式主導の流儀に変換出来る. Algol, Basic, Pascal(Pascalのポインタ変数を使わない時)のような, 合成オブジェクトの扱いの貧弱な言語では, 合成オブジェクトを扱おうとすると, よく命令形の流儀にはまってしまう. 式主導の書式の利点が使えれば, この節でやったように, システムを命令形の流儀で実装しなければならない理由があるか問うかも知れない. 一つの理由は, 非式主導の制約言語には, コネクタオブジェクトの他に, 制約オブジェクトのハンドル(例えばadder手続きの値)があることだ. このことはコネクタの演算を通して間接的にではなく, 制約と直接通信する新しい演算でシステムを拡張しようと思えば, 有用である. 命令形の実装を使って式主導の流儀の実装をするのは容易だが, その逆は極めて困難である.

[ 目次, 前節, 次節, 索引 ]