[ 目次, 前節, 次節, 索引 ]

   最小責任の原則はもっと先まで延ばすことが出来る. 望むなら, 表現の曖昧さを選択子と構成子を設計した後まで残し, Benの表現とAlyssaの表現の両方を使おうと決めることも出来る. しかし両方の表現が一つのシステムに組み込まれたら, 極座標形式のデータと直交座標形式のデータを区別する方法が必要になる. そうでなければ, 例えば(3,4)のmagnitudeを見つけたいといわれたら, 答が(直交座標形式の数と解釈して)5か, (極座標形式の数と解釈して)3か分らない. この区別を実施する直截な方法は, ---記号 ractangularかpolarの--- 型タグ(type tag)をそれぞれの複素数の一部として含ませることである. そうすれば複素数を操作しようとした時, どちらの選択子を使うかをタグを使って決定出来る.

   タグつきデータを操作するには, データオブジェクトからタグと実際の内容(複素数の時は極座標か直交座標)と取り出す手続きtype-tagとcontentsがあると仮定する. 更にタグと内容をとり, タグつきデータを作る手続きattach-tagを仮定する. これを実装する直截な方法は, 通常のリスト構造を使うことである:

(define (attach-tag type-tag contents)
  (cons type-tag contents))


(define (type-tag datum)
  (if (pair? datum)
      (car datum)
      (error "Bad tagged datum -- TYPE-TAG" datum)))


(define (contents datum)
  (if (pair? datum)
      (cdr datum)
      (error "Bad tagged datum -- CONTENTS" datum)))

   これらの手続きを使い, それぞれ直交座標形式と極座標形式の数を認識する手続きrectangular?とpolar?が定義出来る:

(define (rectangular? z)
  (eq? (type-tag z) 'rectangular))


(define (polar? z)
  (eq? (type-tag z) 'polar))

   型タグを使い, BenとAlyssaは自分のプログラムを修正し, 二つの表現が一つのシステムに共存出来るようにした. Benが複素数を構成する時, 彼は直交座標とタグづけする. Alyssaが複素数を構成する時, 彼女は極座標とタグづけする. その上BenとAlyssaは, 手続きの名前が衝突しないようにしなければならない. 一つの方法はBenは各表現手続きの名前にrectangularの添字をつけ, Alyssaは名前にpolarをつけることだ. これが2.4.1節のBenの改定版直交座標表現である:

(define (real-part-rectangular z) (car z))


(define (imag-part-rectangular z) (cdr z))


(define (magnitude-rectangular z)
  (sqrt (+ (square (real-part-rectangular z))
           (square (imag-part-rectangular z)))))


(define (angle-rectangular z)
  (atan (imag-part-rectangular z)
        (real-part-rectangular z)))


(define (make-from-real-imag-rectangular x y)
  (attach-tag 'rectangular (cons x y)))


(define (make-from-mag-ang-rectangular r a) 
  (attach-tag 'rectangular
              (cons (* r (cos a)) (* r (sin a)))))

(define (real-part-polar z)
  (* (magnitude-polar z) (cos (angle-polar z))))


(define (imag-part-polar z)
  (* (magnitude-polar z) (sin (angle-polar z))))


(define (magnitude-polar z) (car z))


(define (angle-polar z) (cdr z))


(define (make-from-real-imag-polar x y) 
  (attach-tag 'polar
               (cons (sqrt (+ (square x) (square y)))
                     (atan y x))))


(define (make-from-mag-ang-polar r a)
  (attach-tag 'polar (cons r a)))

   各汎用選択子は引数のタグを調べ, その型のデータを扱う適切な手続きを呼ぶ手続きとして実装される. 例えば複素数の実部をとるのに, real-part はタグを調べてBenのreal-part-rectangularを使うかAlyssaの real-part-polarを使うか決定する. いずれにしろ裸のタグなしデータをとるのにcontentsを使い, これを必要に応じて直交座標か極座標の手続きに送る.

(define (real-part z)
  (cond ((rectangular? z) 
         (real-part-rectangular (contents z)))
        ((polar? z)
         (real-part-polar (contents z)))
        (else (error "Unknown type -- REAL-PART" z))))


(define (imag-part z)
  (cond ((rectangular? z)
         (imag-part-rectangular (contents z)))
        ((polar? z)
         (imag-part-polar (contents z)))
        (else (error "Unknown type -- IMAG-PART" z))))


(define (magnitude z)
  (cond ((rectangular? z)
         (magnitude-rectangular (contents z)))
        ((polar? z)
         (magnitude-polar (contents z)))
        (else (error "Unknown type -- MAGNITUDE" z))))


(define (angle z)
  (cond ((rectangular? z)
         (angle-rectangular (contents z)))
        ((polar? z)
         (angle-polar (contents z)))
        (else (error "Unknown type -- ANGLE" z))))

   複素数算術演算を実装するのに, 2.4.1節と同じ手続きadd-complex, sub-complex, mul-complexおよびdiv-complexが使えるが, それらが呼ぶ選択子が汎用だからである. そしてどちらの表現も使うことが出来る. 例えば手続きadd-complexは依然として

(define (add-complex z1 z2)
  (make-from-real-imag (+ (real-part z1) (real-part z2))
                       (+ (imag-part z1) (imag-part z2))))

   最後に複素数を構成するのにBenの表現を使うかAlyssaの表現を使うか決めなければならない. 一つの合理的な決め方は実部と虚部があれば直交座標数を構成し, 絶対値と偏角があれば極座標数を構成することだ:

(define (make-from-real-imag x y)
  (make-from-real-imag-rectangular x y))


(define (make-from-mag-ang r a)
  (make-from-mag-ang-polar r a))

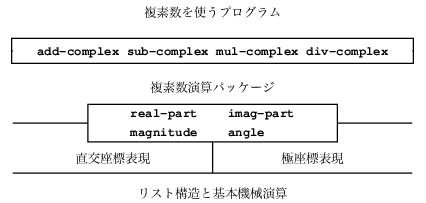
   最終的な複素数システムは, 図2.21に示す構造をしている. システムは三つの相互に独立な部分: 複素数の算術演算, Alyssaの極座標実装, Benの直交座標実装に分割される. 直交座標と極座標の実装は, 別々に作業するBenとAlyssa によって書かれた. これらは複素数算術演算の手続きを, 抽象的な構成子/選択子のインターフェースを使って実装しようとする, 第三プログラマにより, 基盤の表現として利用される.

   各データオブジェクトは, その型でタグづけられているので, 選択子はデータに汎用として演算出来る. 各選択子は, それが作用しようとしている特定の型に従って振舞うように定義されている. 異る表現のインターフェースとなる汎用機構に注意しよう: ある表現実装では(例えばAlyssaの極座標パッケージでは)複素数は型タグなしの対(絶対値, 偏角)である. 汎用選択子がpolar 型の数に演算する時は, タグを剥して, 内容をAlyssaのプログラムに渡す. 逆にAlyssaが, 一般利用のために数を構成する時は, 彼女はそれにタグをつけ, 高レベルの手続きに適切に認識出来るようにする. データオブジェクトをレベルからレベルへ渡す時, タグをつけ剥しするのは, 2.5節で見るように重要な組織化戦略である.

[ 目次, 前節, 次節, 索引 ]