[ 目次, 前節, 次節, 索引 ]

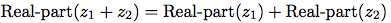
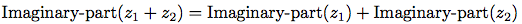
   有理数と同様, 複素数も順序づけられた対で自然に表現出来る. 複素数の集合は直交した二つの軸, 「実」軸と「虚」軸が張る二次元空間と考えることが出来る. (図2.20参照.) この見方では, 複素数z = x + iy(ここにi² = -1) は, 実座標がx, 虚座標がyの平面上の点と考えることが出来る. 複素数の加算は, この表現では, 座標毎の加算になる:

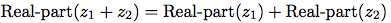
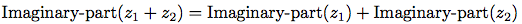
   複素数を掛ける時は, 複素数の絶対値と偏角(図2.20のrとA)による極座標形式での表現を使っての考え方が自然である. 二つの複素数の積は, 一つの複素数をもう一つの複素数の長さで延長し, もう一つの偏角で回転して得たベクトルである:

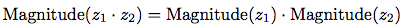
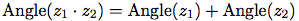
   このように複素数にはそれぞれ異る演算に適した二つの異る表現がある. しかも, 複素数を利用するプログラムを書く人の観点からは, データ抽象の原則により, 複素数を操作する演算は, 計算機がどの表現を使っているかに無関係に使えなければならない. 例えば直交座標で指定してある複素数の絶対値を見ることが出来れば有用なことが多い. 同様に極座標で指定した複素数の実部が分れば有用なことも多い.



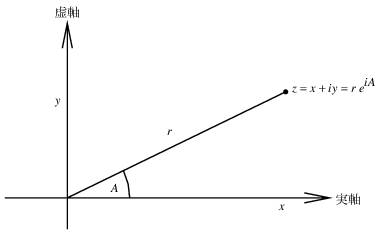
図20 平面上の点としての複素数

   こういうシステムの設計には, 2.1.1節の有理数パッケージの設計で採用したのと同じ データ抽象戦略を採用しよう. 複素数の演算が四つの選択子: real-part, imag-part, magnitudeおよびangleを使って実装してあると仮定しよう. また複素数を構成する二つの手続きがあるとする: make-from-real-imagは実部と虚部で指定した複素数を返し, make-from-mag-angは絶対値と偏角で指定した複素数を返す. この手続きは任意の複素数zについて

(make-from-real-imag (real-part z) (imag-part z))

(make-from-mag-ang (magnitude z) (angle z))

   これらの構成子と選択子を使い, 2.1.1節でやったのと同じように, 構成子と選択子で指定される「抽象データ」を使った複素数の算術演算を実装出来る. 上の式が示すように, 実部と虚部を使って複素数を足し, 引きし, 絶対値と偏角を使って複素数を掛け, 割りする:

(define (add-complex z1 z2)
  (make-from-real-imag (+ (real-part z1) (real-part z2))
                       (+ (imag-part z1) (imag-part z2))))


(define (sub-complex z1 z2)
  (make-from-real-imag (- (real-part z1) (real-part z2))
                       (- (imag-part z1) (imag-part z2))))


(define (mul-complex z1 z2)
  (make-from-mag-ang (* (magnitude z1) (magnitude z2))
                     (+ (angle z1) (angle z2))))


(define (div-complex z1 z2)
  (make-from-mag-ang (/ (magnitude z1) (magnitude z2))
                     (- (angle z1) (angle z2))))

   複素数のパッケージを完成するには, 表現を選び, 素材の数と素材のリスト構造を使って構成子と選択子を実装しなければならない. 二つの明瞭なやり方がある: 複素数を(実部, 虚部)の対で「直交座標形式」でも, (絶対値, 偏角)の対で「極座標形式」でも表現出来る. どちらに決めるか.

   この選択を具体的にするため, 複素数システムの表現を独立に設計している二人のプログラマ, Ben BitdiddleとAlyssa P. Hackerがいるとしよう. Benは複素数を直交座標形式で表現することに決めた. この方法では複素数の実部と虚部の選択は, 複素数を与えられた実部と虚部から構成するのと同様に一目瞭然である. 絶対値と偏角を見つけたり, 与えられた絶対値と偏角から複素数を構成するには, 彼は実部と虚部(x, y)を絶対値と偏角(r, A)に関係づける三角法の関係





を使う.44 そこでBenの表現はそれぞれ次の選択子と構成子で与えられる:

(define (real-part z) (car z))


(define (imag-part z) (cdr z))


(define (magnitude z)
  (sqrt (+ (square (real-part z)) (square (imag-part z)))))


(define (angle z)
  (atan (imag-part z) (real-part z)))


(define (make-from-real-imag x y) (cons x y))


(define (make-from-mag-ang r a) 
  (cons (* r (cos a)) (* r (sin a))))

   一方Alyssaは複素数を極座標形式で表現することに決めた. 彼女にとり, 絶対値と偏角の選択は直截であるが, 実部と虚部を得るのに 三角法の関係を使わなければならない. Alyssaの表現は:

(define (real-part z)
  (* (magnitude z) (cos (angle z))))


(define (imag-part z)
  (* (magnitude z) (sin (angle z))))


(define (magnitude z) (car z))


(define (angle z) (cdr z))


(define (make-from-real-imag x y) 
  (cons (sqrt (+ (square x) (square y)))
        (atan y x)))


(define (make-from-mag-ang r a) (cons r a))

   データ抽象のやり方では, add-complex, sub-complex, mul-complexおよびdiv-complexの同じ実装がBenの表現でもAlyssaの表現でも働くことを保証する.

43 実際のシステムでは直交座標と極座標形式での変換の 丸め誤差のため, 殆んどの場合, 極座標形式より直交座標形式の方が好まれる. これが複素数の例が非現実的である理由である. しかし汎用演算を使うシステムの分りやすい例と, 本章の後の方で開発する, より実質的なシステムへの絶好な導入となる.

44 ここで使う逆正接関数は, Schemeの atan手続きで計算するが, 二つの引数x, yをとり, その正接がy/xになる角度を返す. 引数の符号が角度の象限を決める.

[ 目次, 前節, 次節, 索引 ]