図2.19 複素数システムのデータ抽象の壁
これらのデータ抽象の壁は, 複雑さを制御する強力な道具である. データオブジェクトの基盤の表現を隔離することで, 大きいプログラムを設計する作業を, 分割して行える小さい作業に分けることが出来る. しかし, この種のデータ抽象はまだ十分に強力ではない. データオブジェクトの「基盤の表現」を持ち出すのは, 必ずしもうまくはいかないかも知れない.
一つには, データオブジェクトの有用な表現は複数あるだろうし, 複数の表現を使うシステムが設計したくなるかも知れない. 単純な例をとれば, 複素数は二つの殆んど等価な方法: 直交座標形式(実部と虚部)と極座標形式(絶対値と偏角)で表現出来る. ある時は直交座標形式が適切であり, またある時は極座標形式が適切である. 実際複素数を両方の方式で表現したシステムを考えることは可能で, そこでは複素数を操作する手続きはいずれの表現でも働く.
更に重要なことに, プログラムシステムは長期にわたり, 大勢の人で設計することが多く, 要求は時間と共に変り勝ちである. そういう環境では, データ表現についての選択を誰もが前もって同意することは出来ない. そこで表現を使用から隔離するデータ抽象の壁に加え, 異る設計選択を相互に隔離し, 一つのプログラムの中に, 異る選択が共存出来るようにする抽象の壁が必要になる. その上, 大きいプログラムはしばしば別々に設計された既存の部品を組み合せて作り出すから, プログラマが部品を 加法的に(additively), つまり部品を再設計, 再実装せずに, より大きいシステムへと組み立てる方法が必要である.
本節では, プログラムの異る部分では, 異る方法で表現されているかも知れないデータにどう対処するかを勉強する. そのためには 汎用手続き(generic procedure)---複数の方法で表現されているかも知れないデータに演算する手続き---を構成する必要がある. 汎用手続きを作る主要な技法は, 型タグ(type tag)を持つデータオブジェクト, つまりそれをどう処理すべきかの明示的な表示を持つデータオブジェクトを使って作業することだ. また汎用演算による加法的組立てシステムの強力で便宜的実装戦略である, データ主導(data directed)プログラミングについても論じる.
単純な複素数の例から始めよう. 抽象的「複素数」データオブジェクトの考えを維持しつつ, 型タグとデータ主導流によって複素数の直交座標形式と極座標形式を別々に設計する方法を見よう.
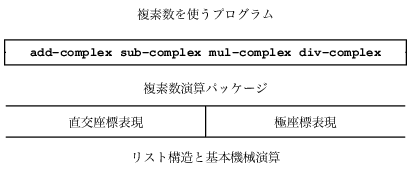
これを行うには, 数がどう表現されているかと独立に, 複素数の部分にアクセスする汎用選択子を使い, 複素数の算術演算(add-complex, sub-complex, mul-complexおよび
div-complex)を定義する. 図2.19に示すように, 結果の複素数システムにはこの別種の壁が出来る.
「水平な」抽象の壁は図2.1に示したものと同じ役割を果す. これは「高レベル」演算を「低レベル」表現から隔離する. それに加え「垂直な」壁があり,
それがいろいろな表現の別々の設計と実装を可能にする.

図2.19 複素数システムのデータ抽象の壁
2.5節では汎用算術演算パッケージ開発のための型タグとデータ主導流の使い方を示す. そこで用意する手続き(add, mul等)は, あらゆる種類の「数」を操作するのに使え, 新しい種類の数が必要になった時, 容易に拡張出来る. 2.5.3節では, 記号代数を実行するシステムでの汎用算術演算の使い方を示す.