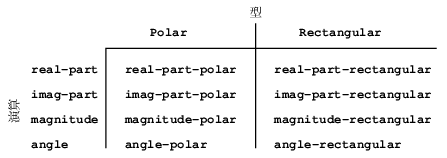
図2.22 複素数システムの演算の表
この技法のもう一つの弱点は, それぞれの表現は別々に設計することは出来るが, システム全体でどの二つの手続きも同じ名前を持たない保証をしなければならないことである. これがBenとAlyssaが2.4.1節の元々の手続きの名前を変えなければならなかった理由である.
これらの弱点が意味するところは, 汎用インターフェースのこの実装法は加法的(additive)ではないということだ. 汎用選択手続きを実装する人は, 新しい表現が組み込まれる度に, 手続きを修正しなければならず, 個々の表現とインターフェースをとる人は, 名前の衝突を避けるため, プログラムを変更しなければならない. これらの場合, プログラムに施すべき変更は一目瞭然ではあるが, とにかくやらなければならず, 不便とエラーの元凶である. これは複素数システムにとり, 現状では大した問題ではないが, 複素数の表現が二つではなく, 数百もあったとしよう. そして抽象データインターフェースで保守すべき, 汎用選択子も多数あるとしよう. 実際, すべてのインターフェース手続き, すべての表現を理解しているプログラマは一人もいないとしよう. 大規模データベース管理システムのようなプログラムでは, このような問題は実在し, 解決しなければならない.
われわれに必要なのは, システム設計を更に部品化する手段である. これにはデータ主導プログラミング(data-directed programming)というプログラム技法が用意されている. データ主導プログラミングがどう働くかを理解するには, 一群の型に共通な一群の汎用演算を扱う時は, 実効的には一方の軸に演算をとり, 他方の軸に型をとった二次元の表を扱っているという見方から始めよう. この表の項目は, 各引数の型に対し, 各演算が実装する手続きである. 前の節で開発したシステムでは, 演算名, 型名と実際の手続きに対応は, 汎用インターフェース手続きの中に拡散されていた. これと同じ情報は, 図2.22に示すように表にまとめることが出来る.
データ主導プログラミングは, このような表で直接働くプログラム設計技法である. 前には, 複素演算プログラムを二つの表現パッケージとインターフェースをとる機構を, 型に従って明白に振り分ける一群の手続きとして実装した. ここでは表から演算名と引数の型の組合せを探し, 作用させるべき正しい手続きを見つけ, それを引数の内容に作用させる単一の手続きとしてインターフェースを実装する. このようにすれば, 新しい表現をパッケージに追加するにも, 既存の手続きを変更する必要はなく, 表に新しい項目を追加するだけでよい.

図2.22 複素数システムの演算の表
この計画を実装するには, 演算対型の表を操作する, 二つの手続きput
とgetがあると仮定する.
•
(put ⟨op⟩ ⟨type⟩ ⟨item⟩)
は⟨item⟩を表の⟨op⟩と⟨type⟩のところに設定する.
•
(get ⟨op⟩ ⟨type⟩)
は表の⟨op⟩と⟨type⟩を探し, そこに見つけたものを返す. なにもなければgetは偽を返す.
ここではputとgetは言語に組み込まれていると仮定しよう. 3章(3.3.3節)で, 表を操作するこの演算や他の演算の実装を見よう.
データ主導プログラミングは複素数システムでは次のように使う. 直交座標表現を開発したBenは, 初め通りにプログラムを実装する. 彼は手続きの集り, つまり パッケージ(package)を定義し, システムの他の部分とはシステムが直交座標数にどう演算するかを指示する表の項目を加えてインターフェースをとる. このことは次の手続きを呼び出すことで実現出来る:
(define (install-rectangular-package)
;; 内部手続き
(define (real-part z) (car z))
(define (imag-part z) (cdr z))
(define (make-from-real-imag x y) (cons x y))
(define (magnitude z)
(sqrt (+ (square (real-part z))
(square (imag-part z)))))
(define (angle z)
(atan (imag-part z) (real-part z)))
(define (make-from-mag-ang r a)
(cons (* r (cos a)) (* r (sin a))))
;; システムの他の部分とのインターフェース
(define (tag x) (attach-tag 'rectangular x))
(put 'real-part '(rectangular) real-part)
(put 'imag-part '(rectangular) imag-part)
(put 'magnitude '(rectangular) magnitude)
(put 'angle '(rectangular) angle)
(put 'make-from-real-imag 'rectangular
(lambda (x y) (tag (make-from-real-imag x y))))
(put 'make-from-mag-ang 'rectangular
(lambda (r a) (tag (make-from-mag-ang r a))))
'done)
この内部手続きは2.4.1節でBenが一人で作業した時に書いたものと同じ手続きであることに注意しよう. システムの他の部分とインターフェースをとるのに, 変更は全く必要ない. 更にこれらの手続き定義は設定手続きの内部にあるので, Benは直交座標パッケージの外の手続きとの名前の衝突を気にすることはない. システムの他の部分とのインターフェースをとるのに, Benはreal-part 手続きを手続き名real-partと型(rectangular)の下に設定した. 他の選択子についても同様である.45 インターフェースは外部のシステムが使う構成子も定義している.46 これらはタグを追加する他はBenの内部で定義した構成子と同じである.
(define (install-polar-package)
;; 内部手続き
(define (magnitude z) (car z))
(define (angle z) (cdr z))
(define (make-from-mag-ang r a) (cons r a))
(define (real-part z)
(* (magnitude z) (cos (angle z))))
(define (imag-part z)
(* (magnitude z) (sin (angle z))))
(define (make-from-real-imag x y)
(cons (sqrt (+ (square x) (square y)))
(atan y x)))
;; システムの他の部分とのインターフェース
(define (tag x) (attach-tag 'polar x))
(put 'real-part '(polar) real-part)
(put 'imag-part '(polar) imag-part)
(put 'magnitude '(polar) magnitude)
(put 'angle '(polar) angle)
(put 'make-from-real-imag 'polar
(lambda (x y) (tag (make-from-real-imag x y))))
(put 'make-from-mag-ang 'polar
(lambda (r a) (tag (make-from-mag-ang r a))))
'done)
BenとAlyssaはお互いに同じ名前(例えばreal-part)で定義した元々の手続きを使っているが, それらの定義は今や異る手続きの内部にあり(1.1.8節参照) 名前の衝突はない.
複素数の算術演算の選択子は, 汎用演算を引数に作用させる apply-genericという一般「演算」手続きを使って表にアクセスする. apply-genericは演算の名前と引数の型から表を探し, 得られた手続きがあればそれを作用させる:47
(define (apply-generic op . args)
(let ((type-tags (map type-tag args)))
(let ((proc (get op type-tags)))
(if proc
(apply proc (map contents args))
(error
"No method for these types -- APPLY-GENERIC"
(list op type-tags))))))
apply-genericを使えば, 汎用選択子を次のように定義出来る:
(define (real-part z) (apply-generic 'real-part z)) (define (imag-part z) (apply-generic 'imag-part z)) (define (magnitude z) (apply-generic 'magnitude z)) (define (angle z) (apply-generic 'angle z))新しい表現がシステムに追加されても, これらは全く変らないことに注意しよう.
またパッケージの外部のプログラムが実部と虚部から, また絶対値と偏角から複素数を作るのに表から構成子を取り出して使うことが出来る. 2.4.2節のように, 実部と虚部がある時には直交座標数を, 絶対値と偏角がある時には極座標数を構成する:
(define (make-from-real-imag x y) ((get 'make-from-real-imag 'rectangular) x y)) (define (make-from-mag-ang r a) ((get 'make-from-mag-ang 'polar) r a))
(define (deriv exp var)
(cond ((number? exp) 0)
((variable? exp) (if (same-variable? exp var) 1 0))
((sum? exp)
(make-sum (deriv (addend exp) var)
(deriv (augend exp) var)))
((product? exp)
(make-sum
(make-product (multiplier exp)
(deriv (multiplicand exp) var))
(make-product (deriv (multiplier exp) var)
(multiplicand exp))))
⟨更に多くの規則をここに追加出来る.⟩
(else (error "unknown expression type -- DERIV" exp))))
このプログラムは微分する式の型による振分けを実行するプログラムと見ることが出来る. その状況ではデータの「型タグ」は(+のような)代数演算の記号で, 実行する演算はderivである. 元の微分手続きを
(define (deriv exp var)
(cond ((number? exp) 0)
((variable? exp) (if (same-variable? exp var) 1 0))
(else ((get 'deriv (operator exp)) (operands exp)
var))))
(define (operator exp) (car exp))
(define (operands exp) (cdr exp))
のように書き直し, このプログラムをデータ主導の形に変換出来る. ((get (operator exp) 'deriv) (operands exp) var)のようにしたとしよう. 微分システムには対応したどのような変更が必要か.
データ主導プログラミングにより, そういう戦略を実装する方法を示せ. 例として各事業所の従業員レコードが, 従業員の名前でキーをつけたレコードの集合からなる一つのファイルで出来ているとする. 集合の構造は事業所毎に異る.
更に各従業員のレコード自体が(事業所毎に異った構造の)集合で,
addressとかsalaryという識別子でキーをつけた情報を含んでいる.
a. 本部のために, 指定した従業員ファイルから, 指定した従業員のレコードを検索するget-record手続きを実装せよ. この手続きはどの事業所のファイルに対しても使えなければならない. それぞれの事業所ファイルはどう構造化すべきか説明せよ. 特にどんな型情報が追加されるべきか.
b. 本部のために, いずれの事業所の従業員ファイルからでも与えられた従業員のレコードから, 給与の情報を返すget-salary手続きを実装せよ. この演算が働くためには, レコードをどう構造化すべきか.
c. 本部のために, find-employee-record手続きを実装せよ. すべての事業所ファイルから与えられた従業員のレコードを探し, それを返すものとする. この手続きは引数として従業員の名前と全事業所ファイルのリストをとるものと仮定せよ.
d. この企業が, 別の会社を合併した時, 新しい従業員情報を中央システムに組み込むには, どういう変更をすべきか.
もう一つの実装戦略は, 表を列方向に分割することで, データの型によって振り分ける「賢明な手続き」を使う代りに, 手続き名によって振り分ける「賢明なデータオブジェクト」で仕事をすることである. それには直交座標数のようなデータオブジェクトを, 入力として必要な演算名をとり, 指示された演算を実行する手続きとして表現するようにする. このやり方では, make-from-real-imagは
(define (make-from-real-imag x y)
(define (dispatch op)
(cond ((eq? op 'real-part) x)
((eq? op 'imag-part) y)
((eq? op 'magnitude)
(sqrt (+ (square x) (square y))))
((eq? op 'angle) (atan y x))
(else
(error "Unknown op -- MAKE-FROM-REAL-IMAG" op))))
dispatch)
のように書ける. これに対応し, 汎用演算を引数に作用させる
apply-generic手続きは, 単に演算の名前をデータオブジェクトに渡し, オブジェクトに仕事をさせるだけである:48
(define (apply-generic op arg) (arg op))make-from-real-imagが返す値は内部のdispatch手続きであることに注意しよう. apply-genericが演算を実行するよう要求した時, この手続きが呼び出される.
このプログラミングの流儀はメッセージパッシング(message passing)
という. この名前はデータオブジェクトが必要な演算の名前を「メッセージ」として受け取る実体であるという連想から来ている. メッセージパッシングの一つの例は2.1.3節のcons, carおよびcdrがデータオブジェクトでなく, 手続きとして定義出来るのを見たところにあった. メッセージパッシングは, 数学的トリックではなく, 汎用演算を使ったシステムを作る有用な技法である. 本章の残りでは, メッセージパッシングではなく, データ主導プログラミングを使って汎用算術演算の議論を続けよう. 3章でメッセージパッシングに戻り, シミュレーションプログラムを構成するのに有用な道具になり得ることを見る.
問題 2.75
構成子make-from-mag-angをメッセージパッシングの流儀で実装せよ. この手続きは上のmake-from-real-imagに似ている筈だ.
問題 2.76
汎用演算を使った巨大システムが発展すると, 新しいデータオブジェクトの型や, 新しい演算が必要になる. 三つの戦略---明白な振分けを持つ汎用演算, データ主導流, メッセージパッシング流---のそれぞれにつき, 新しい型や新しい演算を追加する時, システムに施すべき変更につき述べよ. 新しい型が絶えず追加されるシステムにはどの方法が最も適切か. 新しい演算が絶えず追加されるシステムには, どれが最も適切か.
45
記号rectangularでなく,
リスト(rectangular)を使ったのは, 同一型でない複数個の引数の演算があるかも知れないためだ.
46
構成子が設定される型は, 構成子は常に一つの型のオブジェクトを作るために使うので, リストである必要はない.
47
apply-genericは問題2.20に述べた
ドット末尾記法を使っているが, 異る汎用演算は引数の個数が異るかも知れぬからである. apply-genericではopの値はapply-genericの最初の引数であり, argsの値は残り引数のリストである.
apply-genericは基本手続き
applyを使う. applyは手続きとリストの二つの引数をとる.
applyはリストの要素を引数として手続きを作用させる. 例えば
(apply + (list 1 2 3 4))
は10を返す.
48
この方法の一つの制限は一引数の汎用演算しか出来ないことである.