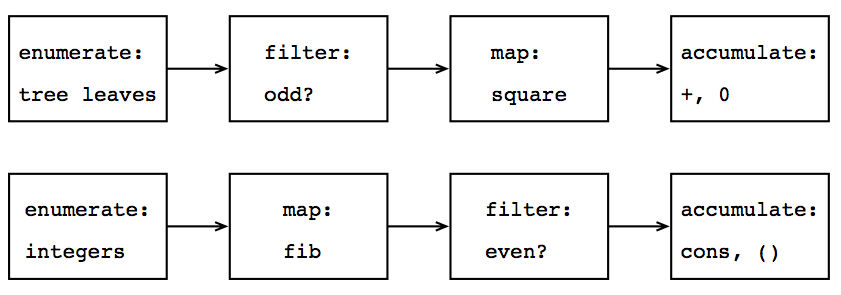
図2.7 手続きsum-odd-squares(上段)とeven-fibs(下段)の信号処理図式は, 両プロセスの間の共通性を浮び上らせる
1.3節で, 高階手続きとして実装したプログラム抽象が, 数値データを扱うプログラムの共通パターンを取り込む様子を見た. 合成データを扱うための類似の演算を形式化する能力は, われわれがデータ構造を操作するスタイルに決定的に依存している. 例えば, 2.2.2節のcount-leaves手続きに類似の, 引数として木をとり, 奇数である葉の二乗の和を計算する手続きを考えよう:
(define (sum-odd-squares tree)
(cond ((null? tree) 0)
((not (pair? tree))
(if (odd? tree) (square tree) 0))
(else (+ (sum-odd-squares (car tree))
(sum-odd-squares (cdr tree))))))
この手続きは次の, 与えられた整数nより小さいか等しいkに対して, 偶数のFibonacci数Fib(k)のリストを作る手続きとは, 一見して非常に違っている:
(define (even-fibs n)
(define (next k)
(if (> k n)
nil
(let ((f (fib k)))
(if (even? f)
(cons f (next (+ k 1)))
(next (+ k 1))))))
(next 0))
この二つの手続きが, 構造的に非常に違っているという事実にも拘らず, 両方の計算のより抽象的な記述から, かなりの類似性が見えてくる. 始めのプログラムは
• 木の葉を数え上げる[enumerate];
• フィルタを通し, 奇数のものを選ぶ;
• 選ばれたものをそれぞれ二乗する;
• 0の初期値に結果を+を使いアキュムレート[accumulate]する.
後のプログラムは
• 整数を0からnまで数え上げる;
• 整数のそれぞれのFibonacci数を計算する;
• フィルタを通し, 偶数のものを選ぶ;
• 空リストの初期値に結果をconsを使いアキュムレートする.
信号処理の技術者は, これらの処理を数珠つなぎの段を流れる信号と考えるのが自然と思うであろう. 各段では, 図2.7のように, プログラムの計画の一部を実装している. sum-odd-squaresでは, 木の葉からなる「信号」を発生する
数え上げ(enumerator)から始る. この信号は奇数でない要素を除去する
フィルタ(filter)を通過する. 出てきた信号は次に
写像(map)を通過するが,これは各要素にsquare手続きを作用させる「変換器」である. 写像の出力は,
アキュムレータ(accumulator)へ入力され, 0から始り, +を使って組み合される. even-fibsの計画も同様である.

図2.7 手続きsum-odd-squares(上段)とeven-fibs(下段)の信号処理図式は, 両プロセスの間の共通性を浮び上らせる
困ったことに上の二つの手続きは, この信号処理構造を示していない. 例えばsum-odd-squares手続きを調べてみると, 数え上げは一部はnull? とpair?テストで, また一部は手続きの木構造再帰を使って実装してある. 同様にアキュムレーションも一部はテストで, また一部は再帰の加算に見ることが出来る. 一般に, どの手続きにも信号処理の記述の要素に対応する, はっきりとした部分はない. この二つの手続きは計算を異る形に分解する. 数え上げを手続き全体にまき散し, 写像, フィルタ, アキュムレータを使って混ぜ合せる. 手続きの中で, 信号処理の構造が明白になるように, プログラムが構成出来れば, 出来上ったプログラムの概念としての明晰性は増大するであろう.
(map square (list 1 2 3 4 5)) (1 4 9 16 25)
与えられた述語を満す要素だけ選択する並びのフィルタは
(define (filter predicate sequence)
(cond ((null? sequence) nil)
((predicate (car sequence))
(cons (car sequence)
(filter predicate (cdr sequence))))
(else (filter predicate (cdr sequence)))))
で達成される. 例えば(filter odd? (list 1 2 3 4 5)) (1 3 5)
アキュムレーションは
(define (accumulate op initial sequence)
(if (null? sequence)
initial
(op (car sequence)
(accumulate op initial (cdr sequence)))))
(accumulate + 0 (list 1 2 3 4 5))
15
(accumulate * 1 (list 1 2 3 4 5))
120
(accumulate cons nil (list 1 2 3 4 5))
(1 2 3 4 5)
と実装される.
信号処理方式の実装で残っているのは処理すべき要素の並びを数え上げることだけだ. even-fibsでは, 与えられた範囲の整数の並びを発生する必要があり, 次のようにする:
(define (enumerate-interval low high)
(if (> low high)
nil
(cons low (enumerate-interval (+ low 1) high))))
(enumerate-interval 2 7)
(2 3 4 5 6 7)
木の葉を数え上げるには
(define (enumerate-tree tree)
(cond ((null? tree) nil)
((not (pair? tree)) (list tree))
(else (append (enumerate-tree (car tree))
(enumerate-tree (cdr tree))))))
(enumerate-tree (list 1 (list 2 (list 3 4)) 5))
(1 2 3 4 5)
が使える.14
さて, sum-odd-squaresとeven-fibsを信号処理方式に形式化し直すことが出来る. sum-odd-squaresでは木の葉の並びを数え上げ, 並びの奇数のものだけを残してフィルタし, 要素のそれぞれを二乗し, 結果の和をとる:
(define (sum-odd-squares tree)
(accumulate +
0
(map square
(filter odd?
(enumerate-tree tree)))))
even-fibsでは0からnまでの整数を数え上げ, これらの整数のそれぞれのFibonacci数を作り, 結果の並びを偶数のものだけを残してフィルタし,
結果をリストにアキュムレートする:
(define (even-fibs n)
(accumulate cons
nil
(filter even?
(map fib
(enumerate-interval 0 n)))))
プログラムを並びの演算として表す価値は, 部品化されたプログラム設計, つまり比較的独立な部品を組み合せて作り上げる設計を可能とすることだ. われわれは,標準部品のライブラリと, 部品を柔軟に接続するための公認インターフェースを用意することで, 部品化された設計を奨励する.
標準部品化された組立ては, 工学設計では, 複雑さを制御する強力な戦略である. 例えば実際の信号処理の応用では, 設計者は通常フィルタや変換器の標準化された部品群の中から選択した素子を, 数珠つなぎにすることでシステムを構築する. 同様に並びの演算は, われわれが取り替え引き替えすることの出来る標準プログラム素子のライブラリを用意する. 例えば sum-odd-squaresとeven-fibsの手続きの部品を, 最初のn+1個のFibonacci数の二乗のリストを作るのに再利用出来る.
(define (list-fib-squares n)
(accumulate cons
nil
(map square
(map fib
(enumerate-interval 0 n)))))
(list-fib-squares 10)
(0 1 1 4 9 25 64 169 441 1156 3025)
部品を再配置し, 並びの中の奇数の二乗の積の計算に使える:
(define (product-of-squares-of-odd-elements sequence)
(accumulate *
1
(map square
(filter odd? sequence))))
(product-of-squares-of-odd-elements (list 1 2 3 4 5))
225
慣習的データ処理も並びの演算を使って形式化出来る. 個人レコードの並びがあり, 最高収入のプログラマの給料を見つけたいとしよう. レコードから給料を返す選択子salaryと, レコードがプログラマのものかをテストする述語programmer?があると仮定する. こういうプログラムが書ける.
(define (salary-of-highest-paid-programmer records)
(accumulate max
0
(map salary
(filter programmer? records))))
以上の例は並びの演算で表すことの出来る, 広範囲の処理のヒントに過ぎない.15
ここでリストとして実装した並びは, 処理部品を組み合せるのを可能にする公認インターフェースとして役立つ. その上, 構造を並びとして一様に表現すると, プログラムのデータ構造依存性を, 少数の並びの演算の中に局所化出来る.
これらを変更して, 並びの別の表現の実験が出来るが, プログラム全体の設計には手をつけないで済む. この能力を3.5節で活用するが, そこでは並びの処理のパラダイムを, 無限の並びが扱えるよう一般化する.
問題 2.33
リスト操作の基本演算の, アキュムレーションとしての定義が以下にある. 欠けた部分を補って完成せよ.
(define (map p sequence) (accumulate (lambda (x y) ⟨??⟩) nil sequence)) (define (append seq1 seq2) (accumulate cons ⟨??⟩ ⟨??⟩)) (define (length sequence) (accumulate ⟨??⟩ 0 sequence))
(define (horner-eval x coefficient-sequence)
(accumulate (lambda (this-coeff higher-terms) ⟨??⟩)
0
coefficient-sequence))
例えばx=2で, 1+3x+5x3+x5の計算は(horner-eval 2 (list 1 3 0 5 0 1))と評価する.
(define (count-leaves t) (accumulate ⟨??⟩ ⟨??⟩ (map ⟨??⟩ ⟨??⟩)))
(define (accumulate-n op init seqs)
(if (null? (car seqs))
nil
(cons (accumulate op init ⟨??⟩)
(accumulate-n op init ⟨??⟩))))

(dot-product v w) 総和∑i viwiを返す;内積は
(matrix-*-vector m v) ti =∑jmijvjであるようなベクタtを返す;
(matrix-*-matrix m n) pij=∑k miknkjであるようなマトリックスpを返す;
(transpose m) nij=mjiであるようなマトリックスnを返す.
(define (dot-product v w) (accumulate + 0 (map * v w)))と定義出来る.17 他のマトリクス演算を計算する次の手続きの欠けた式を補え. (手続きaccumulate-nは問題2.36で定義してある.)
(define (matrix-*-vector m v)
(map ⟨??⟩ m))
(define (transpose mat)
(accumulate-n ⟨??⟩ ⟨??⟩ mat))
(define (matrix-*-matrix m n)
(let ((cols (transpose n)))
(map ⟨??⟩ m)))
(define (fold-left op initial sequence)
(define (iter result rest)
(if (null? rest)
result
(iter (op result (car rest))
(cdr rest))))
(iter initial sequence))
次の値は何か.
(fold-right / 1 (list 1 2 3)) (fold-left / 1 (list 1 2 3)) (fold-right list nil (list 1 2 3)) (fold-left list nil (list 1 2 3))fold-rightとfold-leftが, どのような並びに対しても同じ値を生じるためにopが満たすべき性質は何か.
(define (reverse sequence) (fold-right (lambda (x y) ⟨??⟩) nil sequence)) (define (reverse sequence) (fold-left (lambda (x y) ⟨??⟩) nil sequence))
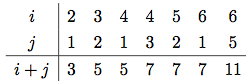
対の並びを作る方法はこうだ: i ≤ nの各整数に, 整数j < iを数え上げ,そういうiとjに対(i, j)を生成する. 並びの演算を使い, 並び (enumerate-interval 1 n)を写像する. この並びの各iに対し, 並び (enumerate-interval 1 (- i 1))を写像する. 後の並びの各jに対(list i j)を生成する. 各iについて対の並びが出来た. すべてのiについての並びを(appendでアキュムレートして)組み合せると望みの対の並びが出来る:19
(accumulate append
nil
(map (lambda (i)
(map (lambda (j) (list i j))
(enumerate-interval 1 (- i 1))))
(enumerate-interval 1 n)))
写像とappendによるアキュムレーションの組合せは, この種のプログラムによくあることだから, 別の手続きとして独立させよう:
(define (flatmap proc seq) (accumulate append nil (map proc seq)))次にその和が素数であるものを見つけるため, 対の並びをフィルタに通す. フィルタの述語は並びの各要素から呼び出される; 引数は対なので, 対から整数を取り出さなければならない. そこで並びの各要素に作用させる述語は
(define (prime-sum? pair) (prime? (+ (car pair) (cadr pair))))最後にフィルタされた対を, 対の二つの要素とその和からなる三つ組を作る次の手続きで写像して, 結果の並びを生成する:
(define (make-pair-sum pair) (list (car pair) (cadr pair) (+ (car pair) (cadr pair))))これらの段取りをすべて結合すると, 完全な手続きが出来る:
(define (prime-sum-pairs n)
(map make-pair-sum
(filter prime-sum?
(flatmap
(lambda (i)
(map (lambda (j) (list i j))
(enumerate-interval 1 (- i 1))))
(enumerate-interval 1 n)))))
写像の入れ子は区間を数え上げるもの以外の並びについても有用である. 集合Sのすべての 順列, つまり集合の要素のすべての並べ方を生成したいとする. 例えば{1, 2, 3}の順列は{1, 2, 3}, {1, 3, 2}, {2, 1, 3}, {2, 3, 1}, {3, 1, 2}, {3, 2, 1}である. Sの順列を生成する計画はこうだ: Sの各要素xに対し, S - xの順列の並びを再帰的に生成し,20 その前にxを連結する. これはSの各xにつき, Sのxで始まる順列の並びを生成する. すべてのxについてこの並びを組み合せると, Sのすべての順列が出来る:21
(define (permutations s)
(if (null? s) ; 空集合?
(list nil) ; 空集合を含むリスト
(flatmap (lambda (x)
(map (lambda (p) (cons x p))
(permutations (remove x s))))
s)))
この戦略が, Sの順列生成問題をSより少ない要素の集合の順列生成問題へ引き下げることに注意しよう. 最後の段階では, 要素の一つもない集合を表す空リストにまで辿りつく. そこでは要素のない集合が一個だけの並び,
(list nil)を生成する. permutationsで使った手続きremoveは並びから指定したものを除いたものを返す. これはフィルタで表せる:
(define (remove item sequence)
(filter (lambda (x) (not (= x item)))
sequence))
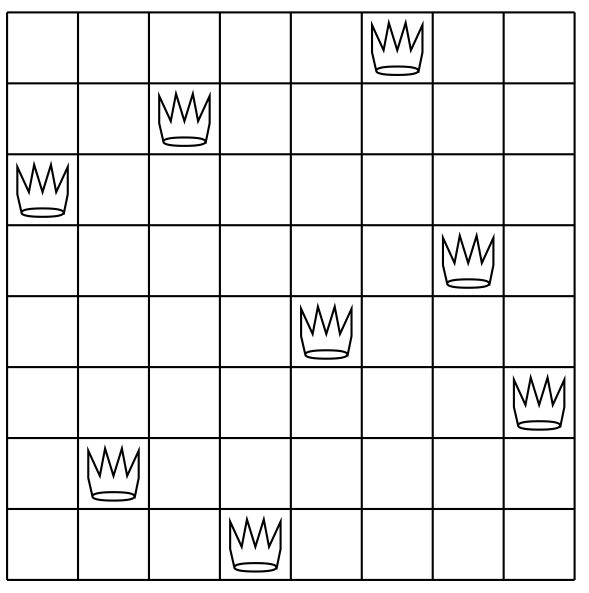
この解の手続きをqueensとして実装する. これはn × nのチェス盤上にnクィーンを置く問題のすべての解の並びを返す. queensの内部手続きqueen-colsは盤の最初のk列にクィーンを置くすべての方法の並びを返す.
(define (queens board-size)
(define (queen-cols k)
(if (= k 0)
(list empty-board)
(filter
(lambda (positions) (safe? k positions))
(flatmap
(lambda (rest-of-queens)
(map (lambda (new-row)
(adjoin-position new-row k rest-of-queens))
(enumerate-interval 1 board-size)))
(queen-cols (- k 1))))))
(queen-cols board-size))
この手続きで, rest-of-queensは最初のk-1列にk-1個のクィーンを置く方法であり, new-rowはk列目にクィーンの置ける行の案である. 盤上の位置の集合の表現を実装し, 位置の集合に新しい場所の座標を連結する手続きadjoin-position, 場所の空集合を表現するempty-boardと合せてプログラムを完成せよ. また, 他のクィーンに対し, k番目のクィーンが安全な場所を決める手続きsafe?を書かなければならない. (他のクィーンは互いに安全であることが保証されているので,
新しいクィーンが安全なことだけ調べればよい.)
(flatmap
(lambda (new-row)
(map (lambda (rest-of-queens)
(adjoin-position new-row k rest-of-queens))
(queen-cols (- k 1))))
(enumerate-interval 1 board-size))
と書いていると指摘した. この入替えがプログラムの実行を遅くする理由を説明せよ. 問題2.42のプログラムがパズルを解く時間をTとし, Louisのプログラムがエイトクィーンパズルを解くのにどのくらいかかるか推定せよ.
14
これはまさに問題2.28の
fringe手続きである. これは一般の並び操作の手続きの一員であることを強調して, 名前をつけ替えた.
15
Richard Waters(1979)は, 写像, フィルタ, アキュムレーションを使って眺めることで, 伝統的な
Fortranプログラムを, 自動的に解析するプログラムを開発した. 彼の発見したところによると, Fortranの科学計算パッケージの90パーセントは, このパラダイムに適している. Lispがプログラム言語として成功した理由の一つは,
高階演算を使って操作出来る順序づけられた集まり[ordered collection]を表す標準媒体を用意したからである. プログラム言語APLも, その能力と人気の多くは似た性格のためである.
APLでは, すべてのデータは配列で表現され, あらゆる配列演算に対して, 万能かつ便利な汎用演算子の集合がある.
16
Knuth(1981)によれば, この方法は十九世紀の初め,
W.G.Hornerが形式化したが, 百年以上も前にNewtonがこの方法を実際に使っている. Hornerの方法は, 最初にanxnを計算し, それにan-1xn-1を足していくなどの直截的方法より少ない回数の加算と乗算で多項式を評価する.
実際, 任意の多項式を評価するどのアルゴリズムも, 少なくてもHornerの方法と同じだけの加算と乗算を使わなければならないことが証明出来, 従ってHornerの方法は多項式評価の
最適アルゴリズムである. (加算の回数については)これは1954年の論文で,
A.M.Ostrowskiが証明し, これが近年の最適アルゴリズム研究を実際に創設した. 乗算について似たような定理は, 1966年に
V.Y.Panが証明した.
Borodinと
Munroの本(1975)には, この最適アルゴリズムや他の結果の概説がある.
17
この定義は脚注12で述べたmapの拡張形を使っている.
18
写像の入れ子のやり方は
David
Turnerが示した. 彼の言語,
KRCと
Mirandaにはこの方法を扱う優美な方式が用意してある. 本節の例(と問題2.42)は, Turner 1981からとった. 3.5.3節で,この解決法を無限の並びへどう一般化するかを示す.
19
ここでは対をLispの対ではなく, 二つの要素のリストで表現している. 「対」(i, j)は, (cons i j)ではなく, (list i j)
で表現してある.
20
集合S - xは,
xを除いたSの要素からなる集合である.
21
Schemeのプログラムでセミコロンは注釈を表す. セミコロンから行の終りまでを解釈形は無視する. 本書では注釈はあまり使わない. プログラムは説明的な名前を使い, 自己文書的にしようと努めている.