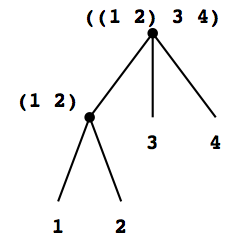
図2.6 木として見た図2.5のリスト構造
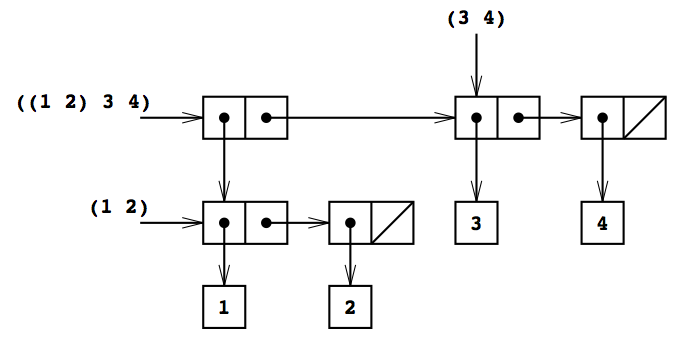
(cons (list 1 2) (list 3 4))で作ったオブジェクト((1 2) 3 4)は, その最初がそれ自身リスト(1 2)である三つの項のリストと見ることが出来る. 実際これは解釈系が印字した形からも分る. 図2.5は, この構造の対を使った表現を示す.
その要素自身が並びであるような並びのもう一つの見方が木(tree)である. 並びの要素は木の枝であり, それ自身並びである要素は部分木である. 図2.6は木として見た図2.5の構造を示す.

図2.6 木として見た図2.5のリスト構造
木に対する演算を, その枝に対する演算へ引き下げ, 更に枝の枝の演算へ引き下げ, 木の葉に至るまで繰り返すことが多いので, 再帰は木構造を扱う自然な道具である. 例えば2.2.1節のlengthの手続きを, 木にある葉の全数を返す count-leaves手続きと比べてみよう.
(define x (cons (list 1 2) (list 3 4))) (length x) 3 (count-leaves x) 4 (list x x) (((1 2) 3 4) ((1 2) 3 4)) (length (list x x)) 2 (count-leaves (list x x)) 8
count-leavesを実装するには, lengthを計算する再帰的計画を思い出してみよう:
• リストxのlengthはxのcdrの
length足す1である.
• 空リストのlengthは0である.
count-leavesも同様である. 空リストに対する値も同じ:
• 空リストのcount-leavesは0.
しかし, 引き下げステップでリストのcarを取り出す時, carはその葉を数えるべき木かも知れないことに注意がいる. そこで適切な引き下げのステップは
• 木xのcount-leavesはxのcarの
count-leaves足すxのcdrのcount-leavesである.
最後にcarをとりながら葉に至るので, もう一つ基本の場合がある:
• 葉のcount-leavesは1である.
木の再帰的手続きを書くのに役立つよう, Schemeには引数が対であるかどうかテストする基本的述語
pair?が用意してある. これが完成した手続きである:13
(define (count-leaves x)
(cond ((null? x) 0)
((not (pair? x)) 1)
(else (+ (count-leaves (car x))
(count-leaves (cdr x))))))
(1 3 (5 7) 9) ((7)) (1 (2 (3 (4 (5 (6 7))))))
(define x (list 1 2 3)) (define y (list 4 5 6))次の式のそれぞれの評価に応じて, 解釈系が印字する結果は何か:
(append x y) (cons x y) (list x y)
(define x (list (list 1 2) (list 3 4))) x ((1 2) (3 4)) (reverse x) ((3 4) (1 2)) (deep-reverse x) ((4 3) (2 1))
(define x (list (list 1 2) (list 3 4))) (fringe x) (1 2 3 4) (fringe (list x x)) (1 2 3 4 1 2 3 4)
(define (make-mobile left right) (list left right))一つの枝はlength(数でなければならない)と, (単なる錘を表現する)数か別のモービルかであるstructureで構成する:
(define (make-branch length structure) (list length structure))a. これに対応する選択子(モービルの枝を返す)left-branchと right-branchと, (枝の部品を返す)branch-lengthと branch-structureを書け.
(define (make-mobile left right) (cons left right)) (define (make-branch length structure) (cons length structure))となるようにモービルの表現を変更したとする. 新しい表現に対応するにはプログラムをどのくらい変更しなければならないか.
(define (scale-tree tree factor)
(cond ((null? tree) nil)
((not (pair? tree)) (* tree factor))
(else (cons (scale-tree (car tree) factor)
(scale-tree (cdr tree) factor)))))
(scale-tree (list 1 (list 2 (list 3 4) 5) (list 6 7))
10)
(10 (20 (30 40) 50) (60 70))
scale-treeを実装するもう一つの方法は, 木を部分木の並びと見, mapを使うことだ. われわれは並びを写像し, 部分木のそれぞれを順に係数倍し,結果のリストを返す. 基底の場合, 木は葉になっているが, 単に係数を掛ける:
(define (scale-tree tree factor)
(map (lambda (sub-tree)
(if (pair? sub-tree)
(scale-tree sub-tree factor)
(* sub-tree factor)))
tree))
木の演算の多くは, 同様な並びの演算と再帰の組合せで実装出来る.
(square-tree
(list 1
(list 2 (list 3 4) 5)
(list 6 7)))
(1 (4 (9 16) 25) (36 49))
square-treeを直接に(つまり高階手続きを使わずに), またmapと再帰を使って定義せよ.
(define (square-tree tree) (tree-map square tree))と定義出来るように, 手続き tree-mapを作れ.
(define (subsets s)
(if (null? s)
(list nil)
(let ((rest (subsets (cdr s))))
(append rest (map ⟨??⟩ rest)))))
13
condの初めの二つの節の順には, 意味がある. 空リストはnull?を満足すると同時に対でもない.