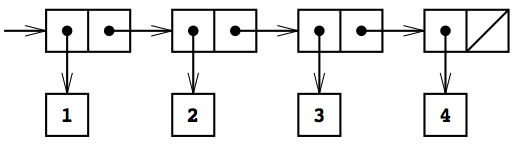
(cons 1
(cons 2
(cons 3
(cons 4 nil))))
入れ子のconsで作られた対の並びを
リスト(list)といい, Schemeはリストを作るのに役立つ
listという基本的手続きを提供する.8
上の並びは(list 1 2 3 4)で作ることが出来る. 一般に
(list ⟨a1⟩ ⟨a2⟩ ...
⟨an⟩)
は
(cons ⟨a1⟩ (cons ⟨a2⟩ (cons
... (cons ⟨an⟩ nil) ... )))
と等価である.
Lispシステムはリストを印字する時は便宜的にかっこで囲まれた要素の並びを印字する. そこで図2.4のデータオブジェクトは(1 2 3 4)と印字される.
(define one-through-four (list 1 2 3 4)) one-through-four (1 2 3 4)式(list 1 2 3 4)と, その式を評価して得たリスト(1 2 3 4)を混同しないよう注意しよう. 式(1 2 3 4)を評価しようとすると, 解釈系が手続き1を引数2, 3と4に作用しようとしたというエラーになる.
carはリストの最初の項を選択し, cdrは先頭の項以外からなる部分リストを選択すると考えてよい. carとcdrの入れ子の作用はリストの二番目, 三番目, それに続く項を取り出すのに使う.9 構成子consは, 先頭に追加の項がつく他は元と同じリストを作る.
(car one-through-four) 1 (cdr one-through-four) (2 3 4) (car (cdr one-through-four)) 2 (cons 10 one-through-four) (10 1 2 3 4) (cons 5 one-through-four) (5 1 2 3 4)対の鎖を終端するのに使うnilの値は要素の一つもない並び, 空リスト(empty list)と考えてよい. nilという言葉はラテン語の「何もない」という意味の語nihilの短縮形である.10
(define (list-ref items n)
(if (= n 0)
(car items)
(list-ref (cdr items) (- n 1))))
(define squares (list 1 4 9 16 25))
(list-ref squares 3)
16
リスト全体をcdrダウンすることもよくある. これに役立つようにSchemeには null?という基本手続きがあり, 引数が空リストかどうかテストする. リストの中にある項の個数を返す手続き lengthは, その典型的な使い方を示す:
(define (length items)
(if (null? items)
0
(+ 1 (length (cdr items)))))
(define odds (list 1 3 5 7))
(length odds)
4
length手続きは単純な再帰的計画で実装してある. 簡約ステップは:
(define (length items)
(define (length-iter a count)
(if (null? a)
count
(length-iter (cdr a) (+ 1 count))))
(length-iter items 0))
もう一つの慣習的プログラミングは, 引数として二つのリストをとり, その要素を結合して新しいリストを作る手続きappendのように, リストを cdrダウンしつつ, 「consアップ」するものである:
(append squares odds) (1 4 9 16 25 1 3 5 7) (append odds squares) (1 3 5 7 1 4 9 16 25)appendは再帰的計画を使っても実装出来る. リストlist1と list2をappendするには, 次を行う:
(define (append list1 list2)
(if (null? list1)
list2
(cons (car list1) (append (cdr list1) list2))))
(last-pair (list 23 72 149 34)) (34)
(reverse (list 1 4 9 16 25)) (25 16 9 4 1)
手続きccを書き直し, その第二引数を, どの硬貨を使うかでなく, 使う硬貨の値のリストとする. 硬貨の種類を定義するリストが作れる.
(define us-coins (list 50 25 10 5 1)) (define uk-coins (list 100 50 20 10 5 2 1 0.5))ccを次のように呼び出す:
(cc 100 us-coins) 292こうするには, プログラムccを多少変える必要がある. 同じ恰好をしているが, 第二引数のアクセスが次のように変る:
(define (cc amount coin-values)
(cond ((= amount 0) 1)
((or (< amount 0) (no-more? coin-values)) 0)
(else
(+ (cc amount
(except-first-denomination coin-values))
(cc (- amount
(first-denomination coin-values))
coin-values)))))
手続きfirst-denomination, except-first-denominationおよびno-more?をリスト構造の基本的演算を使って定義せよ. リスト
coin-valuesの順は, ccの答に影響があるか. なぜか.
(f 1 2 3 4 5 6)を評価すると, fの本体でxは1, yは2, zはリスト(3 4 5 6)になる.
(g 1 2 3 4 5 6)を評価すると, gの本体でwはリスト(1 2 3 4 5 6)になる.11
この記法を使って, 一つかそれを超える個数の整数をとり, 先頭と同じ偶奇性を持つ引数のリストを返す手続きsame-parityを書け. 例えば
(same-parity 1 2 3 4 5 6 7) (1 3 5 7) (same-parity 2 3 4 5 6 7) (2 4 6)
(define (scale-list items factor)
(if (null? items)
nil
(cons (* (car items) factor)
(scale-list (cdr items) factor))))
(scale-list (list 1 2 3 4 5) 10)
(10 20 30 40 50)
この一般的考えを抽象化し, 1.3節のように, 高階手続きとして表した共通パターンに取り込むことが出来る. この高階手続きをmapという. mapは引数として一引数の手続きとリストをとり, その手続きをリストの各要素に作用させて出来た結果のリストを返す:12
(define (map proc items)
(if (null? items)
nil
(cons (proc (car items))
(map proc (cdr items)))))
(map abs (list -10 2.5 -11.6 17))
(10 2.5 11.6 17)
(map (lambda (x) (* x x))
(list 1 2 3 4))
(1 4 9 16)
mapを使ってscale-listを新しく定義出来る:
(define (scale-list items factor)
(map (lambda (x) (* x factor))
items))
mapは共通パターンを取り込んだだけでなく, リストを扱うより高いレベルの抽象化を達成するが故に重要な構成要素である. scale-listの初めの定義では, プログラムの再帰的構造のため, リストの要素ごとの処理に注目させた. mapを使ったscale-listの定義では, そのレベルでの細部を押し隠し, 係数倍が要素のリストを結果のリストに変換することを強調する. 二つの定義の違いは, 計算機が異るプロセスを実行すること(そんなことはないが)ではなく, われわれがプロセスを異って考えることにある. 実際mapは抽象の壁を建て, リストを変換する手続きの実装を, リストの要素をどう取り出し, どう組み合せるかのような細部から隔離する. 図2.1の壁と同様に, この抽象は並びを並びに変換する操作の考え方は保存したまま, 並びをどう実装するかの低レベルの詳細を変更する柔軟さをもたらす. 2.2.3節では, プログラムを構成する枠組として並びの使い方を拡大する.
問題 2.21
手続きsquare-listは引数として数のリストをとり, これらの数の二乗のリストを返す.
(square-list (list 1 2 3 4)) (1 4 9 16)ここにsquare-listの二つの定義がある. 欠けている式を補い, それぞれを完成せよ:
(define (square-list items)
(if (null? items)
nil
(cons ⟨??⟩ ⟨??⟩)))
(define (square-list items)
(map ⟨??⟩ ⟨??⟩))
(define (square-list items)
(define (iter things answer)
(if (null? things)
answer
(iter (cdr things)
(cons (square (car things))
answer))))
(iter items nil))
困ったことにこのsquare-listの定義は, 考えていたのと逆の順に答のリストを作った. なぜか.
Louisはconsの引数を交換して虫をとろうとした:
(define (square-list items)
(define (iter things answer)
(if (null? things)
answer
(iter (cdr things)
(cons answer
(square (car things))))))
(iter items nil))
これも動かなかった. なぜか.
(for-each (lambda (x) (newline) (display x))
(list 57 321 88))
57
321
88
for-eachの呼出しが返す値(上には示さない)は真のような任意のものであってよい. for-eachを実装せよ.
8
本書では, リスト
(list)はリスト終りの印で終端した対の鎖を意味する.
リスト構造(list structure)は反対に, リストだけでなく, 対で作られた任意のデータ構造を指す.
9
carとcdrの入れ子の作用は書くのが煩わしいので, Lispの方言はその省略形を用意している. 例えば
(cadr ⟨arg⟩) = (car (cdr ⟨
arg⟩))
こういう手続きの名前はcで始りrで終る. その間の
aはcar演算, dはcdr演算を表し, 名前に現れる順に作用させる. 名前carとcdrは, cadrのような単純な組合せが発音出来るために生き延びている.
10
注意すべきはLisp方言の標準化で, いかに多くのエネルギーが, 文字通り何もないものの議論に費されたかである. nilは普通の名前であるべきか, nilの値は記号であるべきか, それはリストであるべきか, 対であるべきか.
Schemeではnilは普通の名前であり, 本節ではその値がリスト終りの印である変数として使う. (ちょうどtrueが真の値を持つ普通の変数であるのと同じ.)
CommonLispを含むLispの他の方言では, nilを特別な記号として扱う. 多くの言語の標準化口論に耐えてきた本書の筆者は, この問題を避けて通りたい. 2.3節でクォートを紹介すると, 空リストを'()と書き, 変数nilを完全に排除する.
11
lambdaを使ってfやgを定義するには
(define f (lambda (x y . z) ⟨body⟩))
(define g (lambda w ⟨body⟩))
と書く.
12
Schemeが標準的に用意しているmap手続きは, ここに述べたものより一般的である. より一般的
mapは, n引数の手続きとn個のリストをとり, 手続きをリストのすべての第一要素に作用させ, リストのすべての第二要素に作用させ, 等々させて, 結果のリストを返す. 例えば
(map + (list 1 2 3) (list 40 50 60) (list 700 800 900))
(741 852 963)
(map (lambda (x y) (+ x (* 2 y)))
(list 1 2 3)
(list 4 5 6))
(9 12 15)