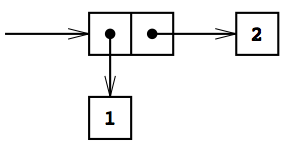
図2.2 (cons 1 2)の箱とポインタ表現

図2.3 対を使って1, 2, 3, 4を組み合せる二つの方法
consは数値だけでなく, 対さえも組み合せることを見た. (問題2.2と2.3でこれを使(うべきであ)った.) 従って, 対はあらゆる種類のデータ構造を構成するための万能構成部品を提供する. 図2.3は対を使って数値1, 2, 3, 4
を組み合せる二つの方法を示す.

図2.2 (cons 1 2)の箱とポインタ表現

図2.3 対を使って1, 2, 3, 4を組み合せる二つの方法
要素が対であるような対を作る能力は, 表現用の道具としてのリスト構造の重要性の本質である. この能力をconsの 閉包性(closure property)という. 一般に, データオブジェクトを組み合せる演算は, その演算を使って何かを組み合せた結果がまた同じ演算を使って組み合せられるという時, 閉包性を満足する.6 閉包はそれにより 階層的(hierarchical)構造---部品から出来た構造で, その部品がまた部品から出来ている---を作ることが出来るために, 組合せのあらゆる面で力の鍵である.
1章の初めから, 非常に単純なプログラム以外は組合せの要素自身がまた組合せであり得るという事実に依っていたから, 手続きを扱うのに閉包性を実質的に使ってきた. 本節では, 合成データの閉包性の重要さを話すことにしよう. 対を使って並びや木を表現する通常の技法を述べ, 閉包性を生き生きと示す図形言語を見せることにしよう.7
6
「閉包」ということばは抽象代数からきている. 集合の要素にある演算を作用させて得られた要素が, またその集合の要素であるなら, 要素の集合はその演算のもとで閉じているという. Lispの社会でも(困ったことに)「閉包」という用語を全く無関係な概念を表すのに使う: そこでは, 閉包は手続きを自由変数と一緒に表現する実装上の技法である. 本書では, 第二の意味での「閉包」という言葉は使わない.
7
組合せのやり方が閉包性を満足すべきだというのは, 直截的な考えだ.
困ったことに多くの普通のプログラム言語にあるデータ組合せ演算は閉包性を満足せず, 閉包性を活用するのは煩わしい.
Fortranや
Basicでは, データ要素を配列にまとめて組み合せられる. しかしその要素が配列であるような配列は作ることが出来ない.
Pascalや
Cでは, その要素が構造である構造は許される. しかしプログラマはポインタをはっきり操作する必要があり, 構造の各フィールドは, 前もって規定した型の要素しか入れることが出来ないという制限を守らなければならない. 対の使えるLispと違って, これらの言語には合成データを一様に操作するのが容易になる基本の汎用の糊はない. この制限が本書の序文にある
Alan Perlisの意見「Pascalでは, 宣言可能なデータ構造の多さが関数の特殊化を惹き起し, それが行きがかりの協調を禁止し処罰する. 一つのデータ構造に働く100個の関数の方が, 10種のデータ構造のそれぞれに働く10個ずつの関数よりありがたい.」の背後にある.