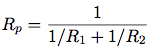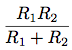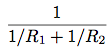電気工学者は, 電気的諸量の計算にAlyssaのシステムを使うとしよう. 二つの抵抗値R1とR2を並列にした等価抵抗値Rpを公式
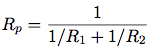
を使って計算することが必要になる時がある. 抵抗値は抵抗の製造者が保証した
許容誤差が判っているのが普通だ. 例えば「10パーセントの許容誤差で6.8オーム」と書いてある抵抗を買えば, 抵抗値は6.8 - 0.68 = 6.12と6.8 + 0.68
= 7.48オームの間の抵抗値を持っているということしか確かでない. そこで6.8オーム10パーセントの抵抗と4.7オーム5パーセントの抵抗を並列にすれば,
合成抵抗は(両抵抗が下限値にある場合)約2.58オームと, (両抵抗が上限値にある場合)約2.97オームの範囲を持つ.
Alyssaの考えは, 区間(不確かな量の可能な値の範囲を表現するオブジェクト) を組み合せる算術演算の組として, 「区間算術演算」を実装することである. 二つの区間の加算, 減算, 乗算または除算の結果はそれ自身, 結果の範囲を表す区間である.
Alyssaは二つの端点: 上限と下限を持つ「区間」という抽象オブジェクトがあると仮定した. 彼女はまた区間の端点が与えられた時, データ構成子 make-intervalを使って区間が構成出来ると仮定した. Alyssaはまず二つの区間を足す手続きを書いた. 彼女は和の最小値は二つの下限の和であり, 最大値は二つの上限の和であると考えた.
(define (add-interval x y)
(make-interval (+ (lower-bound x) (lower-bound y))
(+ (upper-bound x) (upper-bound y))))
Alyssaはまた限界の積の最大値と最小値を見つけ, それらを結果の区間の限界とすることで, 二つの区間の積も作った.
(minとmaxは任意個の引数の最小値と最大値を見つける基本手続きである.)
(define (mul-interval x y)
(let ((p1 (* (lower-bound x) (lower-bound y)))
(p2 (* (lower-bound x) (upper-bound y)))
(p3 (* (upper-bound x) (lower-bound y)))
(p4 (* (upper-bound x) (upper-bound y))))
(make-interval (min p1 p2 p3 p4)
(max p1 p2 p3 p4))))
二つの区間を割るのに, Alyssaは前の値に, 後の値の逆数を掛けた. 逆数の限界は上限の逆数と下限の逆数の順であることに注意しよう.
(define (div-interval x y)
(mul-interval x
(make-interval (/ 1.0 (upper-bound y))
(/ 1.0 (lower-bound y)))))
(define (make-interval a b) (cons a b))である. 実装を完成させるため, 選択子 upper-boundと lower-boundを定義せよ.
虫とりがすむとAlyssaはこのプログラムを使ってくれそうな利用者に見せたが, 彼はこのプログラムは違った問題を解いていると文句をいった. 彼が欲しかったのは, 中央値と許容誤差で表す数を扱うプログラムであった. 例えば[3.35, 3.65]ではなく, 3.5 ± 0.15という区間で仕事がしたいのだ. Alyssaは席に戻り, 別の構成子と選択子を用意してこの問題を解決した.
(define (make-center-width c w) (make-interval (- c w) (+ c w))) (define (center i) (/ (+ (lower-bound i) (upper-bound i)) 2)) (define (width i) (/ (- (upper-bound i) (lower-bound i)) 2))
困ったことに, Alyssaの利用者の殆んどは技術者であった. 実際の工学の状況では, 測定は区間の中央値に対する, 区間の幅の比で計る, 通常小さい不確かさを使う. 技術者は初めの抵抗の例のように, 装置のパラメタをパーセント相対許容誤差で規定する.
問題 2.12
中央値とパーセント相対許容誤差をとり, 望み通りの区間を返す構成子
make-center-percentを定義せよ. また区間のパーセント相対許容誤差を返す選択子percentを定義しなければならない. center選択子は上に示したのと同じでよい.
問題 2.13
パーセント相対許容誤差が小さいと仮定出来る時は, 二つの区間の積の相対許容誤差を, 因子の許容誤差を使って近似する簡単な式があることを示せ. すべての数が正と仮定し, 問題を単純化しよう.
かなりの作業の末, Alyssa P. Hackerは完成したシステムを公開した. 何年かして, すっかり忘れた頃, 彼女は怒った利用者, Lem E. Tweakitから逆上した電話を受けた. Lemは並列抵抗の式は
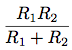
と
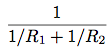
の等価な二つの方法で書けることに気づき, 並列抵抗の式を別々に計算する次の二つのプログラムを書いた:
(define (par1 r1 r2)
(div-interval (mul-interval r1 r2)
(add-interval r1 r2)))
(define (par2 r1 r2)
(let ((one (make-interval 1 1)))
(div-interval one
(add-interval (div-interval one r1)
(div-interval one r2)))))
LemはAlyssaのプログラムが, 二つの計算法で異る結果になると文句をいっている. これはきびしい文句だ.