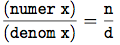
を満たさなければならない. 事実これはmake-rat, numerおよびdenomが有理数表現の適切な基盤となるための唯一の条件である. 一般に, データは選択子と構成子と, これらの手続きを有効な表現とするために満たすべき条件とで定義されると思ってよい.5
ところでデータ(data)とは正しくは何なのか. 「与えられた選択子と構成子で実装されているもの」というのでは不十分だ. 三つの手続きの任意の組が, 有理数の実装の基盤として使えるわけではない.
有理数xを一対の整数nとdから構成したのなら, xからnumerとdenomで取り出して割ったものは, nをdで割ったものと同じになる保証がいる. いいかえれば, make-rat,
numerおよびdenomは, 任意の整数nと任意の零でない整数
dについて, xが(make-rat n d)なら
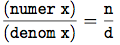
を満たさなければならない. 事実これはmake-rat, numerおよびdenomが有理数表現の適切な基盤となるための唯一の条件である. 一般に, データは選択子と構成子と, これらの手続きを有効な表現とするために満たすべき条件とで定義されると思ってよい.5
この見方は, 有理数のような「高レベル」のデータオブジェクトだけでなく, 下のレベルのオブジェクトの定義にも役立つ. 有理数の定義に使った, 対について考えてみよう. 対が何であるかには触れず, 言語の用意している対の演算の手続きcons, carおよび cdrにだけ触れた. この三つの演算について知らなければならないのは, consを使って二つのオブジェクトを糊づけすれば, そのオブジェクトはcarやcdrを使って取り出せるということである. つまり演算は, 任意のオブジェクトxとyについて, zが(cons x y) なら, (car z)はxであり, (cdr z)はyであるという条件を満たしていなければならない. 事実, この三つの手続きは基本として言語に入っていることを述べた. しかし, 上の条件を満す三つ組の手続きは, 対を実装する基盤として使える. このことはcons, carおよび cdrは他のデータ構造は使わず, 次の手続きだけで実装出来るという事実で示される. 定義を示そう:
(define (cons x y)
(define (dispatch m)
(cond ((= m 0) x)
((= m 1) y)
(else (error "Argument not 0 or 1 -- CONS" m))))
dispatch)
(define (car z) (z 0))
(define (cdr z) (z 1))
この手続きの使い方は, データはどうあるべきかというわれわれの直観には対応しない. それにも拘らず, これが対を表現する正当な方法であることを示すのに必要なのは, これらの手続きが上の条件を満たしていることを示すことだ.
気をつけるべきは(cons x y)の返す値が手続きであることだ. つまり内部的に定義された手続きdispatchで, これは一つの引数をとり, 引数が0か1かによって, xかyを返す. これに対応して, (car z) はzを0に作用させると定義してある. zが(cons x y)で作った手続きなら, 0に作用させたzはxを生じる. そこで希望通り(car (cons x y))はxを生じることが証明出来た. 同様に (cdr (cons x y))は(cons x y)が返した手続きを1に作用させ, yを返す. それ故, 対のこの手続き実装は正当な実装であり, cons, carおよびcdrだけを使って対にアクセスしていれば, 「真の」データ構造を使う実装とは区別出来ない.
対の手続き実装を示しても, われわれの言語がこうなっているというわけではなく, (Schemeも殆んどのLispシステムも, 効率の点から対を直接的に実装している.)こうすることも出来るということだ. 手続き表現は, 解り難くはあるが, 対が満たすべき条件は満たしているので, 対を実装する全く適切な方法である. またこの例は, 手続きをオブジェクトとして操作する能力が自動的に合成データを表現する能力を提供することを示している. これは今は不思議かもしれないが, データの手続き表現はわれわれのプログラミングレパートリの中で,
中心的役割を果すのである. このプログラミングの流儀はしばしば
メッセージパッシング(message passing)といわれ, 3章においてモデリングとシミュレーションを題材とする時, 基本の道具として使うことになる.
問題 2.4
これは対のもう一つの手続き表現である. この表現について任意のオブジェクトxとyに対し, (car (cons x y))がxを生じることを証明せよ.
(define (cons x y) (lambda (m) (m x y))) (define (car z) (z (lambda (p q) p)))これに対するcdrの定義は何か. (ヒント: これが働くことを調べるには, 1.1.5節の置換えモデルを利用せよ.)
(define zero (lambda (f) (lambda (x) x))) (define (add-1 n) (lambda (f) (lambda (x) (f ((n f) x)))))と実装することで, (少なくとも非負の整数だけを問題とする限りは) 数を使わないで済せることが出来ることを考えよう. この表現は発明者 Alonzo Church(λ算法を発明した論理学者)に従い, Church数(Church numerals)として知られている.
(zeroとadd-1を使わずに)oneとtwoを直接定義せよ.
(ヒント: (add-1 zero)を評価するのに, 置換えを使おう.) (add-1の繰返し作用させず)加算手続き+を直接定義せよ.
5
驚くべきことにこの考えを厳密に形式化するのは非常に難しい. 形式化に二つの方法がある. 一つは
C.A.R.Hoare(1972)が開拓したもので,
抽象モデル(abstract model)の方法として知られている. それは上の有理数の例で概観したように, 「手続きと条件」の規定で形式化する. 有理数表現の条件は整数に関する事実(等価と除算)を使って述べていることに注意しよう. 一般に, 抽象モデルは新しい種類のデータオブジェクトを, 前もって定義されたデータオブジェクトの型を使って定義する. データオブジェクトに関する表明はそれを前もって定義されたデータオブジェクトの表明へ引き下げて検査することが出来る. もう一つの方法はMITの
Zilles, IBMの
Goguen,
Thatcher,
Wagnerおよび
Wright(Thatcher, Wagner and Wright 1978参照)とトロントのGuttag
(Guttag 1977参照)が導入したもので,
代数的仕様(algebraic specification)という. これはわれわれの「条件」に対応する公理でシステムの行動を規定する抽象代数システムの要素として「手続き」を見, データオブジェクトに対する表明を検査するのに抽象代数の手法を使う. 二つの方法の紹介は
LiskovとZillesの論文(1975)にある.