[ 目次, 前節, 次節, 索引 ]

   有理数システムの構造を図2.1のように想い描くことが出来る. 水平の線が, システムの異る「レベル」を隔離する抽象の壁(abstraction barrier)である. それぞれのレベルで壁は, データ抽象を使う(上の)プログラムを, データ抽象を実装する(下の)プログラムから分けている. 有理数を使うプログラムは, 有理数パッケージが「公共用」として用意した手続き: add-rat, sub-rat, mul-rat, div-ratおよびequal-rat?だけを使って有理数を操作する. add-ratなどはまた 構成子と選択子make-rat, numerおよびdenomだけを使って実装してあり, 構成子などは, 対を使って実装してある. 対がどう実装してあるかの細部は, 対がcons, carおよびcdrを使って操作出来さえすれば, 有理数パッケージの残りの部分とは無関係である. 効果としては, 各レベルの手続きは, 抽象の壁を定義し, 異るレベルを接続するインターフェースである.




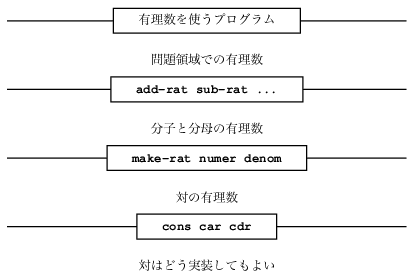
図2.1 有理数パッケージにおけるデータ抽象の壁

   単純な考え方には多くの長所がある. その一つはプログラムの維持, 修正が容易なことである. 複雑なデータ構造は, プログラム言語の用意した基本的データ構造を使い, いろいろな方法で表現出来る. もちろん, 表現の選択はそれに演算するプログラムに影響する; 後になって表現を変えたくなれば, そういうプログラムはすべて然るべく変更しなければならない. こういう作業は大きなプログラムでは, 表現への依存が少数のプログラム部品に押し込められていない限り, 時間も費用もかかる.

   例えば有理数を既約にまで簡約する問題を, 有理数を構成する時ではなく, その部分を取り出す時に行ったとしよう. 構成子と選択子は違う手続きになる.

(define (make-rat n d)
  (cons n d))


(define (numer x)
  (let ((g (gcd (car x) (cdr x))))
    (/ (car x) g)))


(define (denom x)
  (let ((g (gcd (car x) (cdr x))))
    (/ (cdr x) g)))

   表現の依存性を少数のインターフェース手続きに制限すると, プログラムの設計に役立つだけでなく, 別の実装法を考える柔軟さを持ち続けることが出来るため, 修正にも役立つ. われわれの単純な例を使って続けると, 有理数パッケージを設計しており, gcdを構成時か選択時のどちらで実行するか, 初めに決めかねていたとする. データ抽象の技法によれば, 決定を遅らせても, 他の部分を進展させることが出来る.

問題 2.2

平面上の線分を表現する問題を考えよう. 各線分は一対の点: 始発点と終着点で表現されている. 点を使って線分の表現を定義する構成子 make-segmentと選択子 start-segmentと end-segmentを定義せよ. さらに 点は一対の数: x座標とy座標で表現することが出来る. 従ってこの表現を定義する構成子 make-pointと選択子x-pointとy-pointを規定せよ. 最後に選択子と構成子を使い, 引数として線分をとり, 中間点(座標が両端点の座標の平均である点)を返す手続き, midpoint-segmentを定義せよ. その手続きを使ってみるには, 点を印字する方法が必要である.

(define (print-point p)
  (newline)
  (display "(")
  (display (x-point p))
  (display ",")
  (display (y-point p))
  (display ")"))

[ 目次, 前節, 次節, 索引 ]