[ 目次, 前節, 次節, 索引 ]

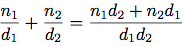
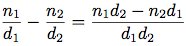
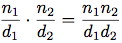
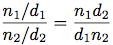
   分子と分母から有理数を作る方法があると仮定して始めよう. また有理数から分子や分母を取り出す(選択する)方法もあるとする. その上, 構成子と選択子は手続き

• (make-rat ⟨n⟩  ⟨d⟩)は分子が整数⟨n⟩, 分母が整数⟨d⟩の有理数を返す.

• (numer ⟨x⟩) 有理数⟨x⟩の分子を返す.

• (denom ⟨x⟩) 有理数⟨x⟩の分母を返す.

として使えるとする.

   ここでは強力な 合成の戦略: 希望的思考(wishful thinking)を使っている. 有理数がどう表現されているか. 手続きnumer, denomやmake-ratがどう実装されているかはまだ話していない. それでもこの三つの手続きがあれば, 次の式を使い, 足し, 引き, 掛け, 割り, 等価をテストすることが出来る:

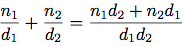
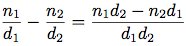
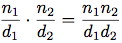
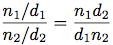
   これらの式を手続きに表せる:

(define (add-rat x y)
  (make-rat (+ (* (numer x) (denom y))
               (* (numer y) (denom x)))
            (* (denom x) (denom y))))


(define (sub-rat x y)
  (make-rat (- (* (numer x) (denom y))
               (* (numer y) (denom x)))
            (* (denom x) (denom y))))


(define (mul-rat x y)
  (make-rat (* (numer x) (numer y))
            (* (denom x) (denom y))))


(define (div-rat x y)
  (make-rat (* (numer x) (denom y))
            (* (denom x) (numer y))))


(define (equal-rat? x y)
  (= (* (numer x) (denom y))
     (* (numer y) (denom x))))

   これで選択子と構成子numer, denomとmake-ratを使って定義した有理数に関する演算が出来た. しかしそれらはまだ定義していない. 分子と分母を糊づけにして, 有理数を作る方法が必要である.

対

(define x (cons 1 2))

(car x)
1

(cdr x)
2

(define x (cons 1 2))

(define y (cons 3 4))

(define z (cons x y))

(car (car z))
1

(car (cdr z))
3

有理数の表現

(define (make-rat n d) (cons n d))


(define (numer x) (car x))


(define (denom x) (cdr x))

(define (print-rat x)
  (newline)
  (display (numer x))
  (display "/")
  (display (denom x)))

(define one-half (make-rat 1 2))

(print-rat one-half)
1/2

(define one-third (make-rat 1 3))

(print-rat (add-rat one-half one-third))
5/6

(print-rat (mul-rat one-half one-third))
1/6

(print-rat (add-rat one-third one-third))
6/9

   最後の例で, われわれの有理数実装は, 有理数を既約にまでは簡約しないことが分る. make-ratを変更して, この点を改善しよう. 1.2.5節のようなgcd手続きがあって, 二つの整数の最大公約数が得られるなら, 対を構成する前に gcdを使い, 分子と分母を既約にまで, 簡約出来る.

(define (make-rat n d)
  (let ((g (gcd n d)))
    (cons (/ n g) (/ d g))))

(print-rat (add-rat one-third one-third))
2/3

2 名前 consは「construct(構成する)」の意である. 名前 carと cdrは IBM 704でのLispの最初の実装からきた. この計算機のアドレス方式は記憶場所の「アドレス」と「デクレメント」が参照出来るようになっていた. carは「Contents of Address part of Register(レジスタのアドレス部)」, cdr(クダーと読む)は「Contents of Decrement part of Register(レジスタのデクレメント部)」を意味する.

3 選択子と構成子を定義するもう一つの方法は

(define make-rat cons)
(define numer car)
(define denom cdr)

最初の定義は名前make-ratを, 対を構成する基本的手続きのconsの値に対応づける. make-ratとconsは同じ基本的構成子の名前となる.

選択子と構成子はこのように定義すると効率はよい: make-ratが consを呼び出すのではなく, make-ratがconsなのである. make-ratが呼び出された時, 二つではなく, 一つの手続きが呼び出される. ところがこうすると, 手続き呼出しをトレースしたり, 手続き呼出しにブレークポイントを設定したりの虫とりツールを使えなくする: make-rat が呼び出されたのは知りたいだろうが, consが呼び出されたすべては知りたくないであろう.

本書では, この形の定義は使わないことにした.

4 displayはデータを印字するSchemeの基本手続きである. Schemeの基本手続きnewlineは改行する. これらの手続きは有用な値は返さないので, 以下のprint-ratの使用例では, print-ratが印字するものだけを示し, print-ratの返す値を解釈系が印字するものは示さない.

[ 目次, 前節, 次節, 索引 ]