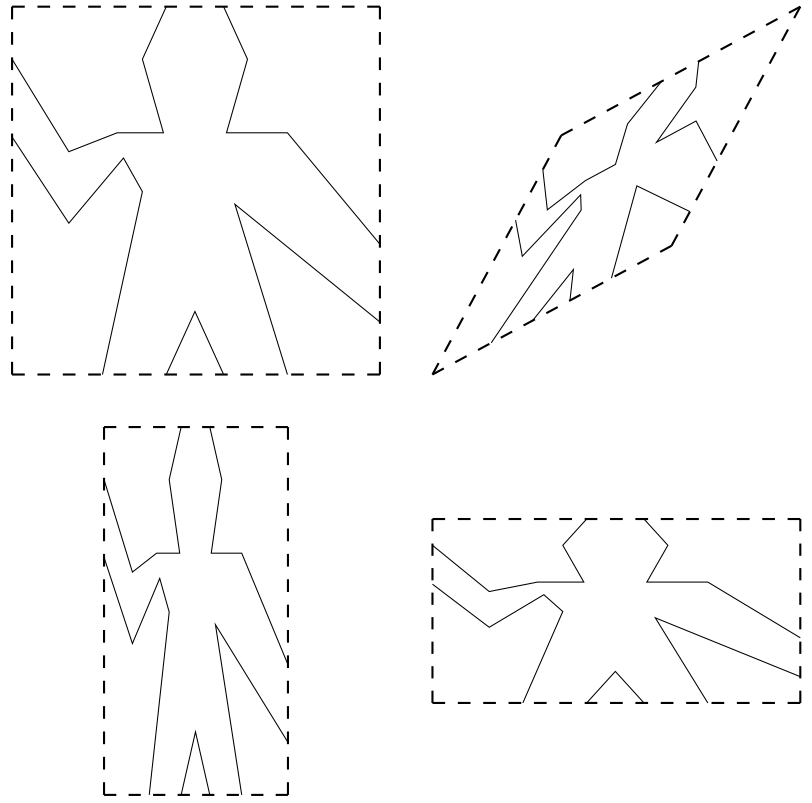
図2.10 四つの異るフレームに対応してwaveペインタが作った画像. 破線で示すフレームは画像の部分ではない.

図2.11 図2.10と同じ四つのフレームに対応して描いたMITの創設者で初代学長であったWilliam Barton Rogersの画像(元の画像はMIT博物館の許可を得て複製した.)
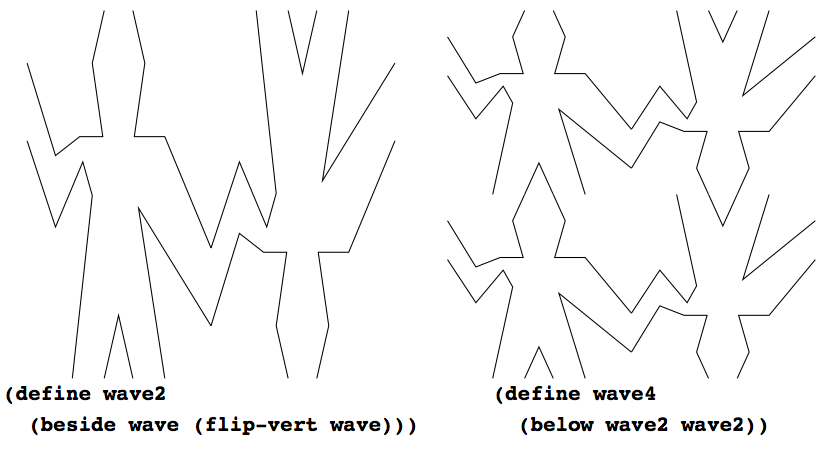
図2.12はwaveから出発し, 二段階で構成したwave4というペインタの描いたものを示す:

この図形言語の美しさの一部は ペインタ(painter)というただ一種の要素しかないことにある. ペインタは規定した並行四辺形の フレームの中に合うように, ずらしたり大きさを変えたりした画像を描く. 例えばwaveという基本的ペインタがあり, 図2.10のような素材の線画を作る. 画の実際の形はフレームに依存する. 図2.10の四枚の画像は同じ waveペインタで作ったものだが, 四つの異るフレームに対応している. ペインタはこれより更にすばらしい: rogersという基本的ペインタは図2.11のようなMITの創始者, William Barton Rogersの絵を描く.23 図2.11の四枚の画像は図2.10のwave画像と同じフレームに対応して描かれた.
画像を組み合せるには, 与えられたペインタから新しいペインタを構成するいろいろな演算を使う. 例えば
beside演算は二つのペインタをとり, 第一のペインタの画像をフレームの左半分に描き, 第二のペインタの画像をフレームの右半分に描く新しい合成ペインタを作り出す. 同様に
belowは二つのペインタをとり, 第一のペインタの画像を第二のペインタの画像の下に描く合成ペインタを作る. いくつかの演算は一個のペインタを変換して新しいペインタを作る. 例えば
flip-vertはペインタを一つとり, その上下逆転の画像を描くペインタを作り,
flip-horizは元のペインタの画像を左右逆転したものを描くペインタを作る.

図2.10 四つの異るフレームに対応してwaveペインタが作った画像.
破線で示すフレームは画像の部分ではない.

図2.11 図2.10と同じ四つのフレームに対応して描いたMITの創設者で初代学長であったWilliam Barton Rogersの画像(元の画像はMIT博物館の許可を得て複製した.)
図2.12はwaveから出発し, 二段階で構成したwave4というペインタの描いたものを示す:
(define wave2 (beside wave (flip-vert wave))) (define wave4 (below wave2 wave2))
ペインタが組み合せられれば, ペインタを組み合せる代表的パターンを抽象化することが出来るようにしたい. ペインタの演算をSchemeの手続きとして実装しよう. このことは図形言語に特別な抽象機構はいらないということを意味する: 組合せの仕方は通常のSchemeの手続きなので, 手続きを使って出来ることなら, ペインタの演算についても何だって出来ることになる. 例えば wave4のパターンを
(define (flipped-pairs painter)
(let ((painter2 (beside painter (flip-vert painter))))
(below painter2 painter2)))
のように抽象化し, wave4は(define wave4 (flipped-pairs wave))のように, このパターンの具体化として定義出来る.
再帰的演算も定義出来る. 図2.13や2.14のようにペインタを右の方へ分割, 枝分れさせるものである:
(define (right-split painter n)
(if (= n 0)
painter
(let ((smaller (right-split painter (- n 1))))
(beside painter (below smaller smaller)))))
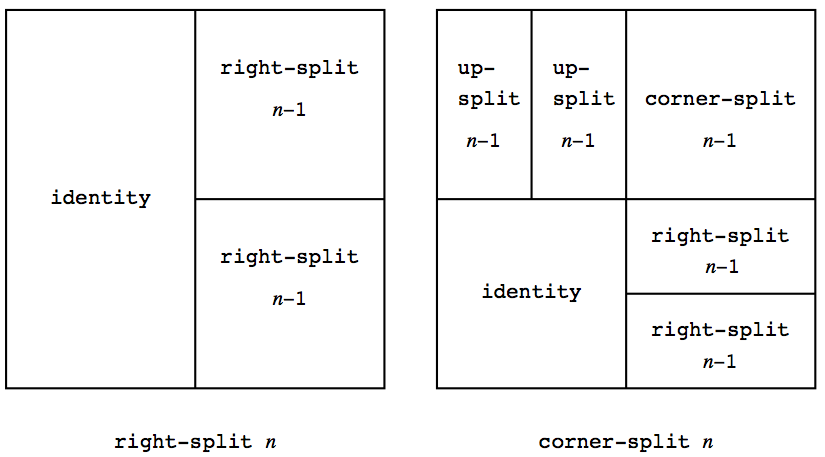
(define (corner-split painter n)
(if (= n 0)
painter
(let ((up (up-split painter (- n 1)))
(right (right-split painter (- n 1))))
(let ((top-left (beside up up))
(bottom-right (below right right))
(corner (corner-split painter (- n 1))))
(beside (below painter top-left)
(below bottom-right corner))))))

(define (square-limit painter n)
(let ((quarter (corner-split painter n)))
(let ((half (beside (flip-horiz quarter) quarter)))
(below (flip-vert half) half))))
例えばflipped-pairsとsquare-limitはどちらもペインタの画像の四つのコピーを四角のパターンの中に配置する; それらはコピーの向きだけが異る. ペインタの組合せのパターンを抽象化する一つの方法は, 次の手続きによるもので, それらは四つの一引数ペインタ演算をとり, 与えられたペインタをこの四つの演算で変換し, 結果を四角の中に配置するペインタ演算を作り出す. tl, tr, blおよびbrはそれぞれ上左コピー, 上右コピー, 下左コピーおよび下右コピーに作用させる変換である.
(define (square-of-four tl tr bl br)
(lambda (painter)
(let ((top (beside (tl painter) (tr painter)))
(bottom (beside (bl painter) (br painter))))
(below bottom top))))
こうなるとflipped-pairsはsquare-of-fourを使い, 次のように定義出来る:24
(define (flipped-pairs painter)
(let ((combine4 (square-of-four identity flip-vert
identity flip-vert)))
(combine4 painter)))
そしてsquare-limitは
(define (square-limit painter n)
(let ((combine4 (square-of-four flip-horiz identity
rotate180 flip-vert)))
(combine4 (corner-split painter n))))
のように表せる.25
(define right-split (split beside below)) (define up-split (split below beside))の評価が, すでに定義したものと同じ振舞いの手続きright-splitとup-splitを作り出すような性質を持つ手続き splitを定義せよ.
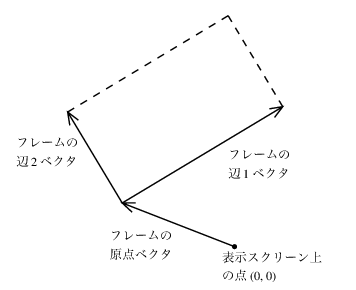
画像を規定するのに単位方形(0 ≤ x, y ≤ 1)の座標を使おう. 各フレームに, 画像をずらし, 大きさを変えてフレームに合せるのに使う
フレーム座標写像(frame coordinate map)を対応づける. 画像はベクタv=(x, y)をベクタ和
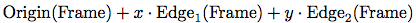
に写像することで, 単位方形をフレームに変換する. 例えば(0, 0)はフレームの原点に, (1, 1)は原点と対角線上の反対にある頂点に, (0.5, 0.5)はフレームの中心に写像される. フレーム座標写像は次の手続きで作ることが出来る:26
(define (frame-coord-map frame)
(lambda (v)
(add-vect
(origin-frame frame)
(add-vect (scale-vect (xcor-vect v)
(edge1-frame frame))
(scale-vect (ycor-vect v)
(edge2-frame frame))))))
frame-coord-mapをフレームに作用させると, ベクタを貰いベクタを返す手続きが返ってくることに注意しよう. 引数のベクタが単位方形にあると, 結果のベクタはフレームにある. 例えば((frame-coord-map a-frame) (make-vect 0 0))は
(origin-frame a-frame)と同じベクタを返す.
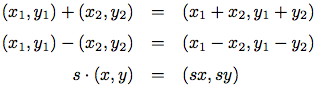
(define (make-frame origin edge1 edge2) (list origin edge1 edge2)) (define (make-frame origin edge1 edge2) (cons origin (cons edge1 edge2)))構成子のそれぞれに, フレームの実装となる適切な選択子を作れ.
基本的ペインタがどう実装してあるかの細部は, 図形システムの性格や描く絵の種類に依存する. 例えばスクリーン上の二つの指定した点の間に線を引く手続き draw-lineがあるとしよう. そうすれば図2.10のwaveペインタのような線画のペインタを, 次のような線分のリストから作り出すことが出来る:27
(define (segments->painter segment-list)
(lambda (frame)
(for-each
(lambda (segment)
(draw-line
((frame-coord-map frame) (start-segment segment))
((frame-coord-map frame) (end-segment segment))))
segment-list)))
線分は単位方形に対する座標を使って与えられている. リスト内の各線分に対してペインタはフレーム座標写像を使い, 線分端点を変換し, 変換された点の間に線を引く.
ペインタを手続きとして表現することは, 図形言語において強力な抽象の壁を建てる. われわれはいろいろな図形機能を使い, 多くの基本的ペインタを作り出し,混合出来る. その実装の細部は関係ない. どんな手続きでも, 引数としてフレームをとり, そのフレームに合うように大きさを変え, 何か描く手続きならペインタとして使える.28
問題 2.48
平面上の有向線分はベクタの対---原点から線分の始点へ向うベクタと, 始点から線分の終点へ向うベクタ---で表現出来る. 問題2.46のベクタ表現を使い,
この線分の表現を構成子
make-segmentと選択子
start-segmentおよび
end-segmentとして定義せよ.
問題 2.49
segments->painterを使い, 次の基本的ペインタを定義せよ:
a. 指定されたフレームの外形を描くペインタ.
b. フレームの向い側の頂点を結んで「X」を描くペインタ.
c. フレームの辺の中点を結んで菱形を描くペインタ.
d. waveペインタ.
ペインタの演算は, 引数としてペインタとフレームの変換法の情報をとり, 新しいペインタを作る手続きtransform-painterに基づく. 変換されたペインタは, フレームに対して呼び出されると, フレームを変換し, 変換されたフレームに対して元のペインタを呼び出す. transform-painterの引数は(ベクタで表現されている)点で, それが新しいフレームの隅を規定する. フレームへ写像されると, 第一の点は新しいフレームの原点を規定し, 後の二点はその辺ベクタの端点を規定する. そこで, 単位方形の中の引数は, 元のフレームに含まれるフレームを規定することになる.
(define (transform-painter painter origin corner1 corner2)
(lambda (frame)
(let ((m (frame-coord-map frame)))
(let ((new-origin (m origin)))
(painter
(make-frame new-origin
(sub-vect (m corner1) new-origin)
(sub-vect (m corner2) new-origin)))))))
ペインタの画像を上下逆転する方法はこうだ:
(define (flip-vert painter)
(transform-painter painter
(make-vect 0.0 1.0) ; 新しいorigin
(make-vect 1.0 1.0) ;edge1の新しい端点
(make-vect 0.0 0.0))) ;edge2の新しい端点
transform-painterを使えば, 新しい変換を定義するのは簡単だ. 例えば与えられたフレームの右上の四半分に画像を縮めるペインタを定義することが出来る:
(define (shrink-to-upper-right painter)
(transform-painter painter
(make-vect 0.5 0.5)
(make-vect 1.0 0.5)
(make-vect 0.5 1.0)))
他には画像を反時計回りに90度回転する変換:29
(define (rotate90 painter)
(transform-painter painter
(make-vect 1.0 0.0)
(make-vect 1.0 1.0)
(make-vect 0.0 0.0)))
や, あるいは画像をフレームの中央へ押し込む変換:30
(define (squash-inwards painter)
(transform-painter painter
(make-vect 0.0 0.0)
(make-vect 0.65 0.35)
(make-vect 0.35 0.65)))
がある.
フレーム変換は二つまたはそれ以上のペインタの組合せ手段を定義する鍵ともなる. 例えばbeside手続きは二つのペインタをとり, それらをそれぞれ引数フレームの左と右半分に描くように変換し, 新しい合成ペインタを作る. 合成ペインタは, フレームを貰うと, まず第一の変換されたペインタを呼び出し, フレームの左半分に描かせ, 次に第二の変換されたペインタを呼び出し, フレームの右半分に描かせる:
(define (beside painter1 painter2)
(let ((split-point (make-vect 0.5 0.0)))
(let ((paint-left
(transform-painter painter1
(make-vect 0.0 0.0)
split-point
(make-vect 0.0 1.0)))
(paint-right
(transform-painter painter2
split-point
(make-vect 1.0 0.0)
(make-vect 0.5 1.0))))
(lambda (frame)
(paint-left frame)
(paint-right frame)))))
ペインタのデータ抽象, 特にペインタの手続きとしての表現が, besideの実装を容易にしているところをよく見よう. beside手続きは, 要素ペインタについての細部はそれぞれのペインタが指示されたフレームに何か書くということ以外, 何も知らなくてよい.
問題 2.50
ペインタを水平に逆転する変換flip-horizと, ペインタを反時計回りに180度と270度回転する変換を定義せよ.
問題 2.51
ペインタに対してbelow演算を定義せよ. belowは引数として二つのペインタをとる. 結果のペインタはフレームを貰うと, 第一のペインタでフレームの下に描き, 第二のペインタで上に描く. belowを二つの異った方法で---
まず上のbesideに似た方法で, 次にbesideと(問題2.50の)適切な回転演算を使って---定義せよ.
また言語とプログラムの設計に重要な別の考えも少しは見た. これは 成層設計(stratified design)の考えである. つまり複雑なシステムは, それぞれの言語を使って記述出来るレベルの並びとして構造化されるべきだという考え方である. 各レベルは, そのレベルで基本的と見なせる部品を組み合せて構成する. また各レベルで構成される部品は, 次のレベルで基本要素として使われる. 成層設計の各レベルで使う言語は基本要素, 組合せ手段, その細部のレベルに適した抽象手段を持つ.
成層設計は複雑システムの工学に広くいきわたっている. 例えば計算機工学では, 抵抗やトランジスタが組み合され, (またアナログ回路の言語を使って記述され,) アンドゲートやオアゲートのような部品を作り出し, ゲート類がディジタル回路設計の言語の基本要素となる.31 これらの部品が組み合されて, プロセッサ, バス回路, メモリーシステムを構成する. それらがまた, 計算機アーキテクチャに適した言語を使って組み合され, 計算機を構成する. 計算機はネットワーク相互接続に適した言語を使って組み合され, 分散システムを構成する.
成層設計の小さい例として, 図形言語はsegments->painterのための線分のリストを作る点や線を規定する言語や, rogersのようなペインタのための詳細な濃淡法を使って作り出された基本要素(基本ペインタ)を使う. われわれの図形言語の大部分は, beside やbelowのような幾何学的組合せ子を使ってのこれらの基本要素の組合せに絞られていた. またbesideやbelowを, square-of-fourのような演算が幾何学的組合せ子を組み合せる共通パターンを取り込む言語で操作される基本要素と見て, 高いレベルで仕事をした.
成層設計は, プログラムを頑健(robust)に作るのに役立つ. つまり仕様の小規模な変更は, なるべくプログラムの相応な小規模な変更しか必要としないようにする. 例えば図2.9に示すwaveに基づく画像を変更したかったとする. waveの要素の細かい形を変えようとする最低レベルで作業することも出来る; corner-splitがwaveを複製する方法を変えようとする中レベルで作業することも出来る; square-limitが隅の四つのコピーをどう配置するかという最高レベルで作業することも出来る. 一般に, 成層設計の各レベルには, システムの性格を表す語彙, それを変更する異った種類の能力がある.
問題 2.52
図2.9に示したwaveのsquare-limitを, 上に示した各レベルで作業して変更せよ. 特に
a. 問題2.49の基本的waveペインタに(例えば笑っているような)線分を加えよ.
b. corner-splitで構成されるパターンを(例えば二つでなく,
up-splitとright-splitのコピーを使うことで)変更せよ.
c. square-limitでsquare-of-fourを使う版を, 隅を異るパターン(例えばRogers氏を, 四角の隅では外側を向せるように)修正せよ.
22
この図形言語は
M.C.Escherの木版「Square Limit」のような画像を構成すべく,
Peter Hendersonが創作した言語に基づいている(Henderson 1982参照). この木版は, 本節のsquare-limit手続きを使って描かれた配置と似た, 大きさを変えつつ繰り返すパターンで構成してある.
23
William Barton Rogers(1804--1882)はMITの創設者で, また初代総長であった.
地質学者として, また才能ある教師として彼はWilliam and Mary大学とバージニア大学で教えた. 1859年にボストンへ移り, そこでは研究の時間が増え,
「工科大学」設立を計画し, マサチューセッツで最初のガスメータの州検査官を勤めた.
1861年にMITが設立されると, 初代総長に選ばれた. Rogersは古典を重要視することで, 当時の他の大学教育とは異る「有用な学習」の考えを支持した. それは彼の書いたところによると「自然科学と社会科学における, 広範, 高度でより実用的な教育と訓練の方法に参加する」ものであった. この教育はまた商業学校の狭い教育からも異る筈であった. Rogersは書いている:
世間の押しつける実用的な研究者と科学的な研究者の区別はまったく下らない. またモダンタイムズの経験は全体としてまったくの無価値を示した.
Rogersは健康上の理由で退職する1870年まで総長を勤めた. 二代目総長 John Runkleが, 1873年の恐慌でもたらされた財政危機の圧力と, HarvardによるMITの乗っとりの試みとの戦いでの働き過ぎで1878年に退任し, Rogersは戻って1881年まで総長の職にあった.
Rogersは1882年の卒業式の予行で, 大学院のクラスに演説中, 崩れ折れて亡くなった. Runkleは同年行われた追悼演説でRogersの最後の言葉を引用した.
Francis A. Walker(第三代MIT総長)の言葉:「本日ここに来て, 工科大学の現状を見ると, 私は科学の最初を思い出す. 私の記憶では百五十年前, Stephen Halesは輝くガスについてパンフレットを出版した. その中で彼がいうには彼の研究が示したのは128粒の 瀝青炭が---」
「瀝青炭」これが彼の最後の言葉であった. その時彼は前のテーブルのノートを見ようとするかのように前に屈み, またゆっくり直立の姿勢に戻りながら手をふり, この世の労働と勝利の情景から, 生命の神秘が解明され肉体から離れた精神が無限の未来の新しくしかも不可解な神秘を熟考しながら永遠の満足を見出す「死の向う」へ移された.
24 等価的に次のようにも書ける.彼は人生を忠実に勇敢に生き, 装いを尽くし, 己の職場で, 公職の中に, 騎士さえも望むような高貴な死を遂げた.
(define flipped-pairs (square-of-four identity flip-vert identity flip-vert))25 rotate180はペインタを180度回転する(問題2.50参照). rotate180の代りに問題1.42のcompose手続きを使って(compose flip-vert flip-horiz)とすることも出来る.