[ 目次, 前節, 次節, 索引 ]

1.3.2 lambdaを使う手続きの構築

1.3.1節のsumを使うのに, 高階手続きの引数として使うためだけにpi-termやpi-nextのような瑣末な手続きを定義しなければならないのは煩わしい. pi-termやpi-nextを定義するより「入力を4だけ増やして返す手続き」とか「入力に, 入力に2足したものを掛け, その逆数を返す手続き」を直接指定する方法があればずっと便利であろう. 手続きを作り出す特殊形式lambdaを使えばそれが出来る. lambdaを使うと欲しかったものは
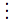
(lambda (x) (+ x 4))
とか
(lambda (x) (/ 1.0 (* x (+ x 2))))
と書ける. そうするとpi-sumは補助の手続きを定義せずに

(define (pi-sum a b)
  (sum (lambda (x) (/ 1.0 (* x (+ x 2))))
       a
       (lambda (x) (+ x 4))
       b))
と書ける.

   またlambdaを使うと, 補助の手続きadd-dxを定義せずに


(define (integral f a b dx)
  (* (sum f
          (+ a (/ dx 2.0))
          (lambda (x) (+ x dx))
          b)
     dx))
と書ける.

   一般的にlambdaは, 手続きに名前がつかない他は, defineと同様に手続きを作り出すのに使う. 

(lambda (⟨formal-parameters⟩) ⟨body⟩)
で出来上る手続きはdefineで作られたものと全く同じ手続きである. 唯一の相違は環境で名前と対応づけられていないことである. 実際 
(define (plus4 x) (+ x 4))
は
(define plus4 (lambda (x) (+ x 4)))
と等価である. lambda式は次のように読める: 
(lambda  (x)            (+    x    4))
↑       ↑             ↑    ↑   ↑
手続き   xを引数とする  を足す x と 4

   手続きを値として持つ式のように, lambda式は

((lambda (x y z) (+ x y (square z))) 1 2 3)
12
のような組合せや, また更に一般に通常は手続き名を使う文脈で演算子として使える.53
局所変数を作り出すletの使い方
lambdaのもう一つの使い方は局所変数を作り出すことにある. 仮パラメタとして束縛されたもの以外にも, 手続きに局所的な変数が欲しくなることがある. 例えば関数



が計算したかったとしよう. これは



と書ける. fを計算する手続きを書くのに, 局所変数としてxとyだけでなく, aとbのような途中の値の名前を入れておきたい. このための一つの方法は補助手続きを使い, 局所変数を束縛することだ: 
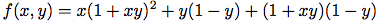
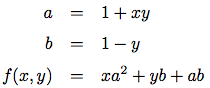
(define (f x y)
  (define (f-helper a b)
    (+ (* x (square a))
       (* y b)
       (* a b)))
  (f-helper (+ 1 (* x y)) 
            (- 1 y)))

   もちろん局所変数の束縛には名なしの手続きを指定するためのlambda式が使える. fの本体はその手続きの呼出しだけとなる: 

(define (f x y)
  ((lambda (a b)
     (+ (* x (square a))
        (* y b)
        (* a b)))
   (+ 1 (* x y))
   (- 1 y)))
この形は有用なので, letという特殊形式が更に便利に使えるようにしている. letを使うとf手続きは
(define (f x y)
  (let ((a (+ 1 (* x y)))
        (b (- 1 y)))
    (+ (* x (square a))
       (* y b)
       (* a b))))
と書ける. letの一般形は

(let (⟨var1⟩ ⟨exp1⟩)
(⟨var2⟩ ⟨exp2⟩)
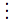(⟨varn⟩ ⟨expn⟩))
  ⟨body⟩)

で, これは

⟨body⟩の中で
⟨var1⟩は値⟨exp1⟩を持ち
⟨var2⟩は値⟨exp2⟩を持ち

⟨varn⟩は値⟨expn⟩を持つとせよ.

と読むと思えばよい. let式の最初の部分は名前と式の対のリストである. letが評価される時, 名前は相対する式の値と対応づけられる. letの本体はこれらの名前が局所変数として束縛されているところで評価される. これは丁度let式がもう一つの構文

((lambda (⟨var1⟩ ... ⟨varn⟩)
     ⟨body⟩)
  ⟨exp1⟩
  
  ⟨expn⟩)

で解釈されることである. 解釈系に局所変数を用意する新しい機構が必要になるわけではない. let式は基盤となるlambda作用の構文シュガーに過ぎない.

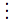
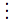
   この等価関係からlet式で指定された変数の有効範囲は, letの本体であることが分る. つまり:

• letは変数をそれが使われる場所に出来るだけ局所的に束縛する. 例えばxの値が5なら, 式

(+ (let ((x 3))
     (+ x (* x 10)))
   x)
の値は38である. letの本体でxは3で, let式の値は33. 一方外側の+の第二引数のxはまだ5である.

• 変数の値はletの外側で計算される. 局所変数の値を用意する式が, 局所変数と同じ名前の変数に依存している時, 問題となる. 例えばxの値が2なら, 式
(let ((x 3)
      (y (+ x 2)))
  (* x y))
の値は, letの本体内でxは3で, (外側のx足す2の)y は4だから, 12になる.

   時にはletと同じ効果を得るため内部定義を使うことがある. 例えば上の手続きfを

(define (f x y)
  (define a (+ 1 (* x y)))
  (define b (- 1 y))
  (+ (* x (square a))
     (* y b)
     (* a b)))
と定義してもよかった. しかし内部defineは内部手続きのためだけにし, このような状況ではletを使いたい.54

問題 1.34

手続き
(define (f g)
  (g 2))
を定義したとする. その時
(f square)
4

(f (lambda (z) (* z (+ z 1))))
6
解釈系に組合せ(f f)を(意地悪く)評価させるとどうなるか. 説明せよ.


53 Lispを学ぶ人にはlambdaより, make-procedureのようなもっと明白な名前であったら, ずっとわかりやすく,強迫感も少かったろう. しかしこの習慣は強固に防護されている. この記法は数理論理学者 Alonzo Church(1941)の数学形式論, λ算法から取り込まれた. Churchは関数と関数作用の概念を研究するための厳密な基盤としてλ計算を考え出した. λ計算はプログラム言語の意味論を数学的に研究する基本的道具になっている.

54 プログラムがわれわれの意味していると思うことを意味していることが確かである程に内部定義を十分理解するには, 本節で述べた評価のプロセスより精巧なモデルが必要である. 手続きの内部定義ではこの微妙さは生じない. 評価について更に学んだ後, 4.1.6節でこの問題に戻ることにする.

[ 目次, 前節, 次節, 索引 ]