[ 目次, 前節, 次節, 索引 ]

区間二分法による方程式の零点の探索

(define (search f neg-point pos-point)
  (let ((midpoint (average neg-point pos-point)))
    (if (close-enough? neg-point pos-point)
        midpoint
        (let ((test-value (f midpoint)))
          (cond ((positive? test-value)
                 (search f neg-point midpoint))
                ((negative? test-value)
                 (search f midpoint pos-point))
                (else midpoint))))))

   初めに関数fと, 値が負と正の二点が与えられているとする. まず二点の中間点を計算する. 次に区間が十分小さいかを調べ, そうであれば単に中間点を答として返す. そうでなければ中間点におけるfの値をテスト値として計算し,テスト値が正なら初めの負の点から中間点までの新しい区間で作業を続ける. テスト値が負なら中間点から正の点までの区間で続ける. 最後にテスト値が丁度0の可能性もあり, その場合は中間点そのものがわれわれの探している解である.

   終端点が「十分近い」かどうかのテストには, 1.1.7節の平方根の計算に使ったものと似た手続きが使える.55

(define (close-enough? x y)
  (< (abs (- x y)) 0.001))

   searchは, うっかりするとfが要求された符号を持たない二点を与えられたりするから, 直接使うには厄介であり, その場合正しくない答が出る. その代りsearchを終端点のどちらが負の関数値で, どちらが正の関数値かを調べ, searchを正しく呼ぶ次の手続きを経て使うことにする. 関数が与えられた二点で同じ符号を持つなら, 区間二分法は使われず, 手続きはエラーとなる.56

(define (half-interval-method f a b)
  (let ((a-value (f a))
        (b-value (f b)))
    (cond ((and (negative? a-value) (positive? b-value))
           (search f a b))
          ((and (negative? b-value) (positive? a-value))
           (search f b a))
          (else
           (error "Values are not of opposite sign" a b)))))

   次の例は2と4の間のsin x = 0の根としてπの近似値をとるのに区間二分法を使う.

(half-interval-method sin 2.0 4.0)
3.14111328125

次の例は区間二分法を使い, 1と2の間で方程式x³ - 2x - 3 = 0の根を探す.

(half-interval-method (lambda (x) (- (* x x x) (* 2 x) 3))
                      1.0
                      2.0)
1.89306640625

関数の不動点の探索

(define tolerance 0.00001)


(define (fixed-point f first-guess)
  (define (close-enough? v1 v2)
    (< (abs (- v1 v2)) tolerance))
  (define (try guess)
    (let ((next (f guess)))
      (if (close-enough? guess next)
          next
          (try next))))
  (try first-guess))

(fixed-point cos 1.0)
.7390822985224023

(fixed-point (lambda (y) (+ (sin y) (cos y)))
             1.0)
1.2587315962971173

   不動点のプロセスは, 1.1.7節で平方根を求めるのに使ったプロセスを思い出させる. どちらも結果がある条件になるまで予測値を繰り返し改良するという考えに基づく. 実際, 平方根の計算をすぐに不動点探索に書き直せる. あるxの平方根の計算はy² = xなるyを探すことである. この方程式を等価な形y = x/yと書き, 関数y x/y~58 の不動点を探しているのだと思えば, 平方根の計算を

(define (sqrt x)
  (fixed-point (lambda (y) (/ x y))
               1.0))

   残念ながら, この不動点探索は収束しない. 最初の予測値をy₁としよう. 次の予測値はy₂ = x/y₁で, その次の予測値はy₃ = x/y₂ = x/(x/y₁) = y₁. つまり答のまわりで振動しながら, 二つの予測値, y₁とy₂を何度も繰り返す無限ループになる.

   そういう振動を制御する一つの方法は予測値の大きな変化を防ぐことである. 答は予測値yとx/yの間にあるから, yからx/y程は遠くない新しい予測値をyとx/yの平均とすることが出来る. つまりyの次の予測値はx/yではなく, ½(y + x/y)である. そのような予測値の並びを作るプロセスは単にy ½(y + x/y)の不動点を探すことである:

(define (sqrt x)
  (fixed-point (lambda (y) (average y (/ x y)))
               1.0))

   この修正により, 平方根の手続きは働く. 実際この定義を解明してみると, ここで生成した平方根の近似値の並びは, 1.1.7節の平方根の初めの手続きが生成するものとまったく同じであることが分る. 解への逐次近似を平均化する方法を 平均緩和法(average damping)というが, 不動点探索で収束を助けることが多い.

問題 1.35

(1.2.2節の)黄金比φが変換x 1 + 1/xの不動点であることを示し, この事実を使いfixed-point手続きにより&\phi;を計算せよ.

問題 1.36

問題1.22で示した基本のnewlineとdisplayを使い, 生成する近似値を順に印字するようfixed-pointを修正せよ. 次にx log(1000)/log(x)の不動点を探索することで, x^x = 1000の解を見つけよ. (自然対数を計算するSchemeの基本log手続きを使う.) 平均緩和を使った時と使わない時のステップ数を比べよ. ({ fixed-pointの予測値を1にして始めてはいけない. log(1)=0による除算を惹き起すからだ.)

問題 1.37

a. 無限の連分数(continued fraction)は



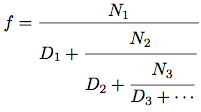
の形の式である. 例えばN_iとD_iがすべて1の無限連分数展開が1/φになることが示せる. φは(1.2.2節で示した)黄金比. 無限連分数の近似値のとり方の一つは, 与えられた項数で展開を中断することで, そういう中断--- k項有限連分数(k-term finite continued fraction)という---は



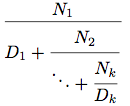
の形である. nとdを一引数(項の添字i)で連分数の項のN_iとD_iを返す手続きとする. (cont-frac n d k)がk項有限連分数を計算するような手続きcont-fracを定義せよ.

(cont-frac (lambda (i) 1.0)
           (lambda (i) 1.0)
           k)

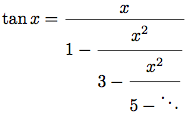
55 0.001を計算の受け入れられる誤差の許容量を示す「小さい」数の代表としてきた. 実際の計算の適切な許容量は解くべき問題と計算機やアルゴリズムの限界に依存する. これは 数値解析の専門家やある種の魔術師の助けを必要とする微妙な問題である.

56 これは引数にエラーメッセージとして印字するいくつかの項目をとる errorを使って実現出来る.

57 講義がつまらない時にやってみるとよい: 電卓をラジアンモードにし, 不動点が得られるまでcosのボタンを押し続ける.

58 (「写像する」と読む)は lambdaの数学者流の記法である. y x/y$は(lambda (y) (/ x y))のことで, つまりyでの値がx/yの関数のことである.

[ 目次, 前節, 次節, 索引 ]