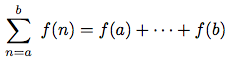
がこの概念を表す. 総和記号の表現力は, 数学者に, 特定の和を扱うのでなく, ---例えば加算する特定の級数とは無関係に総和の一般的結果を導くというような---総和自身の概念を扱うことを可能にした.
(define (sum-integers a b)
(if (> a b)
0
(+ a (sum-integers (+ a 1) b))))
二番目のは与えられた範囲の整数の三乗の和を計算する:
(define (sum-cubes a b)
(if (> a b)
0
(+ (cube a) (sum-cubes (+ a 1) b))))
三番目のは級数の項の並びの和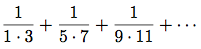
(define (pi-sum a b)
(if (> a b)
0
(+ (/ 1.0 (* a (+ a 2))) (pi-sum (+ a 4) b))))
三つの手続きは明らかに共通の基本パターンを持っている. 手続き名と, 加算される項を計算するaの関数と, aの次の値を用意する関数が違うだけで, 後は殆んどの部分が同じである. 同じ雛型:
(define (⟨name⟩ a b)
(if (> a b)
0
(+ (⟨term⟩ a)
(⟨name⟩ (⟨next⟩ a) b))))
のスロットを埋めることでそれぞれの手続きが生成出来る.
こういう共通なパターンがあるということは, 表舞台に引き出されるのを待っている有用な抽象がある強い証拠である. 数学者は遥か昔に
級数の総和(summation of a series)という抽象を見出し
「総和記号」を発明した. 例えば:
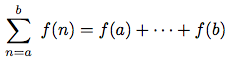
がこの概念を表す. 総和記号の表現力は, 数学者に, 特定の和を扱うのでなく,
---例えば加算する特定の級数とは無関係に総和の一般的結果を導くというような---総和自身の概念を扱うことを可能にした.
同様にプログラムの設計者として, われわれは言語が十分強力で, 特定の和を表現する手続きでなく, 総和自身の概念を表現する手続きが書けるようにしたい. われわれの手続き言語では, 上のような雛型をとり, 「スロット」を仮パラメタに変えることでそれがすぐに出来る:
(define (sum term a next b)
(if (> a b)
0
(+ (term a)
(sum term (next a) next b))))
sumは引数として下限と上限のaとbとともに, 手続き
termとnextをとることに注意しよう. sumは他の手続きのように使える. 例えば(引数を1増やす手続きincとともに)sum-cubesを定義するのに使える:
(define (inc n) (+ n 1)) (define (sum-cubes a b) (sum cube a inc b))これを使えば1から10までの整数の三乗の和が計算出来る:
(sum-cubes 1 10) 3025項を計算する恒等手続きidentityの助けを借り, sumを使ってsum-integersが定義出来る:
(define (identity x) x) (define (sum-integers a b) (sum identity a inc b))そうすると1から10までの整数が足せて:
(sum-integers 1 10) 55同様にpi-sumも定義出来る:50
(define (pi-sum a b)
(define (pi-term x)
(/ 1.0 (* x (+ x 2))))
(define (pi-next x)
(+ x 4))
(sum pi-term a pi-next b))
これらの手続きを使えばπの近似値が計算出来る:
(* 8 (pi-sum 1 1000)) 3.139592655589783
sumがひと度出来ると, これは更なる概念を作るための構成部品となる.
例えばa, b間の関数fの定積分は数値的には式
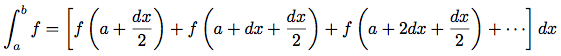
を使ってdxの小さい時の近似値が得られる. これを手続きとして表現出来て:
(define (integral f a b dx)
(define (add-dx x) (+ x dx))
(* (sum f (+ a (/ dx 2.0)) add-dx b)
dx))
(integral cube 0 1 0.01)
.24998750000000042
(integral cube 0 1 0.001)
.249999875000001
(0と1の間のcubeの積分の正確な値は1/4である. )
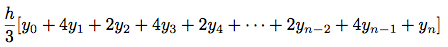
(define (sum term a next b)
(define (iter a result)
(if ⟨??⟩
⟨??⟩
(iter ⟨??⟩ ⟨??⟩)))
(iter ⟨??⟩ ⟨??⟩))
(accumulate combiner null-value term a next b)を使い, 項の集りを組み合せるaccumulateという更に一般的なものの特殊な場合であることを示せ. accumulateは引数としてsumや productと同様, 項と範囲指定と, 先行する項のアキュムレーションと現在の項をどう組み合せるかを指定する(二引数の)combiner手続き, 項がなくなった時に使う値を指定するnull-valueをとる. accumulateを書き, sumやproductがaccumulateの単なる呼出しで定義出来ることを示せ.
49
通常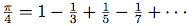
と書くこの級数はLeibnizによる. 3.5.3節で, すばらしい数値トリックがこの級数に基づいているのを見る.
50
pi-nextとpi-termの定義を(これらの手続きは他の目的に使うことはなさそうなので)pi-sumの中に定義するのにブロック構造(1.1.8節)を使っていることに注意しよう. これらを全部取り除く方法は1.3.2節で見る.
51
問題1.31--1.33の意図は, 一見異る演算を, 適切な抽象を使って統合することで達成された表現力を明示することである. しかしアキュムレーションとフィルタは素晴らしい着想ではあるが, これらの抽象のために組み合せる手段を提供するデータ構造を持っていないので, 現時点ではこれらの使用は多少不自由である. この問題には2.2.3節で更に強力な抽象を構築するためフィルタやアキュムレータを組み合せるインターフェースとして,
並び(sequences)の使い方を見た時に戻ることにしよう. これらの方法がプログラム設計の強力で優美な解決法としてすぐにそれらと融合するのが分る.
52
この公式は十七世紀, 英国の数学者
John Wallisが見つけた.