[ 目次, 前節, 次節, 索引 ]

(define (fib n)
  (cond ((= n 0) 0)
        ((= n 1) 1)
        (else (+ (fib (- n 1))
                 (fib (- n 2))))))

    この計算パターンを考える. (fib 5)を計算するには(fib 4)と(fib 3)を計算する. (fib 4)を計算するには (fib 3)と(fib 2)を計算する. 一般に進化するプロセスは図1.5のように, 樹木状に進化する. (一番下を除いた)各レベルで枝は二つに分れることに注意しよう; 手続きfibは起動される度に自分を二回呼び出すという事実を反映している.




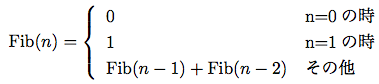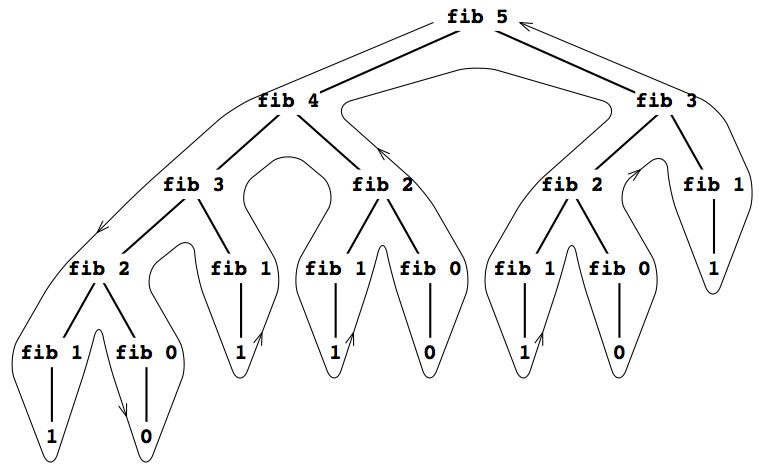
図1.5　(fib 5)の計算で生成された木構造再帰プロセス

    この手続きは代表的な木構造再帰として教育的であるが, あまりに冗長な計算をするから, Fibonacci数の計算としてはひどい方法だ. 図1.5を見ると (fib 3)の計算は---全体の半分くらいの作業だが---完全に重複している. 手続きが葉のところの(fib 1)や(fib 0)を計算する回数は, 正確にFib(n + 1)回であるのを示すのは容易だ. これがいかに悪いかをFib(n)の値がnに 指数的に増加することで示せる. より精密には(問題1.13参照)Fib(n)はφⁿ/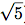に最も近い整数である. ただし



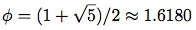
は 黄金比(golden ratio)であり,

φ² = φ + 1

を満す. つまりプロセスは入力に指数的に増加するステップ数が必要である. 一方, 必要なスペースは, 計算中どの節が上方に残っているかを覚えておけばよいので, 入力に線形にしか増加しない. 一般に, 木構造再帰的プロセスで必要なステップ数は木構造の節の数に比例し, 必要なスペースは木構造の最大深さに比例する.

    Fibonacci数の計算の反復的プロセスを形式化することも出来る. 二つの整数a, bをFib(1)=1, Fib(0)=0で初期化し,

a ← a+b
b ← a

の同時の変換を繰り返すのである. n回の変更のあと, a, bはそれぞれFib(n+1), Fib(n)に等しいことを示すのは容易である. そこで手続き

(define (fib n)
  (fib-iter 1 0 n))

(define (fib-iter a b count)
  (if (= count 0)
      b
      (fib-iter (+ a b) a (- count 1))))

    このことから木構造再帰は使いものにならないと決めてはいけない. 数値ではなく, 階層構造のデータを扱うプロセスを考える時, 木構造再帰は自然で強力な道具であることを知る.32 数値演算であっても, 木構造再帰はプログラムの理解や設計を支援してくれるという点で有益である. 例えば最初のfib手続きは二番目のより効率は悪いが, Fibonacci数列の定義の殆んどそのままLispへ変換しただけで, ずっと直截的である. 反復的アルゴリズムの形式化には, 計算を三つの状態変数を使う反復へ作り替えられることに気がつく必要がある.

例: 両替の計算

    この問題は再帰的手続きとして単純な解がある. 使える硬貨をある順に並べたとしよう. すると次の関係が成り立つ:

n種類の硬貨を使う, 金額aの両替の場合の数は:

• 最初の種類の硬貨以外を使う, 金額aの両替の場合の数, 足す

• dを最初の硬貨の額面金額[denomination]として, n種類の硬貨を使う, 金額a - dの両替の場合の数

    これがなぜ正しいかは, 両替が, 最初の硬貨を使わないのと, 使うのの二つのグループに分けられることに注意する. そこである金額の両替の場合の総数は, その金額の最初の硬貨を使わない両替の場合の数足す, 最初の硬貨を使った場合の数に等しい. ところで後者は, 最初の硬貨を使った後に残っている金額の両替の場合の数に等しい.

    かくして, ある金額の両替の問題を, 少ない種類の硬貨を使う少ない金額の問題へ再帰的に縮小させることが出来る. この縮小化を注意深く考察し, 次の縮退した場合が規定出来れば, アルゴリズムが書けることを確認せよ.33

• aがちょうど0なら, 両替の場合の数は1

• aが0より少なければ, 両替の場合の数は0

• nが0なら, 両替の場合の数は0

この記述は容易に再帰的手続きに翻訳出来る.

(define (count-change amount)
  (cc amount 5))

(define (cc amount kinds-of-coins)
  (cond ((= amount 0) 1)
        ((or (< amount 0) (= kinds-of-coins 0)) 0)
        (else (+ (cc amount
                     (- kinds-of-coins 1))
                 (cc (- amount
                        (first-denomination kinds-of-coins))
                     kinds-of-coins)))))

(define (first-denomination kinds-of-coins)
  (cond ((= kinds-of-coins 1) 1)
        ((= kinds-of-coins 2) 5)
        ((= kinds-of-coins 3) 10)
        ((= kinds-of-coins 4) 25)
        ((= kinds-of-coins 5) 50)))

(count-change 100)
292

    count-changeはfibの最初の実装のような冗長な木構造再帰的プロセスを生成する. (292が計算されるまで, かなり時間がかかる.) 一方この解を計算するよりよいアルゴリズムをどう設計するかは明白ではなく, それを挑戦問題としておこう. 木構造再帰プロセスは極めて非効率だが, 規定し理解するのは容易だという観察から, 木構造手続きを同じ結果を計算するより効率的な手続きに変換する「スマート翻訳系」を設計することで, 両世界の長所だけをとろうという提案に駆り立てる.34

問題 1.11

n<3に対してf(n)=n, n ≥ 3に対してf(n)=f(n - 1) + 2 f(n - 2) + 3 f(n - 3)なる規則で定義する関数fがある. 再帰的プロセスの方法でf を計算する手続きを書け. 反復的プロセスの方法でfを計算する手続きを書け.

問題 1.12

次の数のパターンをPascal三角形(Pascal's triangle)という.


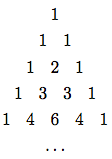
三角形の辺上の数はすべて1, 三角形の内部の数はその上の二つの数の和である.35 再帰的プロセスの方法でPascal三角形の要素を計算する手続きを書け.

問題 1.13

φ= (1+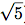)/2としてFib}(n)がφⁿ /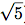に最も近い整数であることを証明せよ. ヒント: ψ= (1-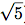)/2とする. 帰納法とFibonacci数の定義(1.2.2節参照)を用い, Fib}(n)=(φⁿ-ψⁿ)/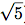を証明せよ.

32 一つの例は1.1.3節にヒントがあった. 解釈系自身は式を木構造再帰的プロセスを使って評価するのである.

33 5 セントと1セントを使って10セントの両替を作る場合を使い, 縮小規則の働きを詳細に調べよ.

34 冗長な計算に対処する一つの方法は, 計算出来たところから自動的に表を構成する仕掛けを作ることである. ある引数に対し手続きを作用させる場合, まずその値が表にあるかを見, その場合, 冗長な計算を回避することが出来る. この方法は テーブル化(tabulation)とかメモ化 (memoization)として知られ, 直接的な方法で実装出来る. テーブル化は(count-changeのような)指数的ステップ数を必要とする手続きを, 記憶容量と時間が入力に線形に増加する手続きに翻訳するのに使われる. 問題3.27参照

35 Pascal三角形の要素を, n行目が(x + y)ⁿの展開の項の係数になっているので, 二項係数(binomial coefficients)という. 係数の計算のこのパターンは Blaise Pascalの1653年の確率論のセミナーの文献 Traité du triangle arithmétique に現れる. Knuth(1973)によると, 同じパターンは中国の数学者 Chu Shih-chieh(朱世傑)が1303年に発表した Szu-yuen Yü-chien (「四元玉鑑」)と, 12世紀のペルシャの詩人で数学者の Omar Khayyamの仕事と, 12世紀のヒンズーの数学者 Bháscara Áchárya の仕事に現れる.

[ 目次, 前節, 次節, 索引 ]