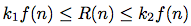
なるnと独立な正の定数k1, k2があれば, R(n)はΘ (f(n))の増加の程度だといい, R(n) = Θ (f(n))と書く. (「シータ f(n)」と読む.) (別のいい方をすれば, 大きいnではR(n)はk1 f(n) とk2 f(n) に挟れている.)
nを問題の大きさを表すパラメタ, R(n)を大きさnの問題に対してプロセスが 必要とする資源の量とする. 前の例でいえば, nをそれに対して関数を計算しようとする数にしたが, 別のものにする可能性もある. 例えば目的がある数の平方根の近似値を計算することなら, nを要求する精度の桁数にするかも知れない. 行列の乗算では, nを行列の行の数にするかも知れない. 一般に, 問題には, プロセス解析をするのに望ましいいろいろな性質がある. 同様にR(n)も使用する内部記憶の数を計るかも知れないし, 実行した基本機械演算の数かも知れない. 一時には決った数の演算しか出来ない計算機では, 必要な時間は実行した基本機械演算数に比例する.
十分大きなnの値に対し,
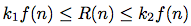
なるnと独立な正の定数k1, k2があれば, R(n)はΘ (f(n))の増加の程度だといい, R(n) = Θ (f(n))と書く. (「シータ f(n)」と読む.) (別のいい方をすれば, 大きいnではR(n)はk1 f(n) とk2
f(n) に挟れている.)
例えば1.2.1節で述べた階乗計算の線形再帰的プロセスのステップ数は, 入力nに比例して増加する. 従ってこのプロセスの必要とするステップ数はΘ(n)で増加する. また必要なスペースもΘ(n)で増加した. 反復的階乗では, ステップ数はやはりΘ(n)だが, スペースはΘ(1), つまり定数であった.36 木構造のFibonacci計算はΘ(φn)ステップと, Θ(n)スペースを必要とする. ここにφは1.2.2節で述べた黄金比である.
増加の程度はプロセスの振舞いのざっとの記述しか与えない. 例えばn2ステップが必要なプロセスも, 1000 n2ステップが必要なプロセスも, 3 n2
+ 10 n + 17ステップが必要なプロセスもすべてΘ(n2)の増加の程度という. だが他方, 増加の程度は問題の大きさを変えた時, プロセスの振舞いをどう予測するかの有効な指示を与える.
Θ(n)の(線形の)プロセスでは, 大きさを倍にすれば, 使う資源もおよそ倍になる.
指数プロセスでは, 問題の大きさの一単位の増加で, 資源の利用が定数倍になる. 1.2節の残りの部分で, 問題の大きさを倍にしても資源の要求が一定量しか増えない,
対数的な増加の程度の二つの問題を見ていこう.
問題 1.14
1.2.2節のcount-change手続きが11セントの両替の場合に生成するプロセスを示す木構造を描け. 両替の金額の増加につれ, このプロセスが使うスペースとステップ数の増加の程度は何か.
問題 1.15
(ラジアンで表す)角度の正弦は, xが十分小さい時, sin x ≈ xの近似と, 正弦の引数の値を小さくするための三角関係式
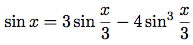
を使って計算出来る. (この問題のためには, 角度の大きさが0.1ラジアンより大きくなければ「十分小さい」と考える.) この方法は次の手続きに採用してある:
(define (cube x) (* x x x))
(define (p x) (- (* 3 x) (* 4 (cube x))))
(define (sine angle)
(if (not (> (abs angle) 0.1))
angle
(p (sine (/ angle 3.0)))))
a. (sine 12.15)の評価で, 手続きpは何回作用させられたか.
36
この説明は極端に単純化してある.
例えばプロセスのステップ数を「機械演算」で考えるなら, われわれは, 乗算を実行するのに必要な機械演算数は掛けられる数の大きさに無関係と仮定しているが, 数がかなり大きければ, これは正しくない. 同様な注意はスペースの推測にも当てはまる. プロセスの設計と記述のように, プロセスの解析も多くの抽象レベルの下で行われる.