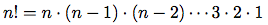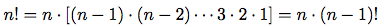[ 目次, 前節, 次節, 索引 ]

1.2.1 線形再帰と反復


で定義する階乗関数から始めよう. 階乗を計算する方法は多い. 一つの方法は任意の正の整数nに対し, n!はnに(n - 1)!を掛けたものとの考えを使うことである.

つまりn!は(n - 1)!を計算し, その結果にnを掛けて計算出来る. 1! は1に等しいという規定を追加すれば, 手続きに変換出来て, 

(define (factorial n)
  (if (= n 1)
      1
      (* n (factorial (- n 1)))))
この手続きが6!を計算しているところ見るには, 図1.3のように, 1.1.5節の置換えモデルが使える.



図1.3　6!を計算する線形再帰プロセス

    階乗の計算の別の見方をしよう. n!の計算の規則を, まず1に2を掛け, 結果に3を掛け, 4を掛け, nになるまで続けるとの規定で記述出来る. より形式的には, 1からnまでを数えるカウンタと共に部分積を保持する. 計算はカウンタと積を, あるステップから次へ,

積 ← カウンタ ・ 積

カウンタ ← カウンタ + 1

の規則に従って同時に変化させ, n!はカウンタがnを超えた時の積の値であるということで記述出来る.

    この記述を階乗計算の手続きとして書き直す:29 


(define (factorial n)
  (fact-iter 1 1 n))

(define (fact-iter product counter max-count)
  (if (> counter max-count)
      product
      (fact-iter (* counter product)
                 (+ counter 1)
                 max-count)))
前と同様, 6!の計算のプロセスの視覚化に, 図1.4のように, 置換えモデルが使える.




図1.4　6!を計算する線形反復プロセス

    二つのプロセスを比べてみよう. ある見方ではそれらは殆んど違わない. 両者は同じ定義域を持つ同じ数学関数を計算し, どちらもn!を計算するのにn に比例したステップを必要とする. 実際どちらも同じ部分積の列を作りながら, 同じ乗算の列を実行する. ところが二つのプロセスの「形」を考える時, それらは全く違って進化することが分る.

    最初のプロセスでは, 置換えモデルは図1.3の矢印で示すように膨張と, それに続く収縮の形をとる. 膨張はプロセスが 遅延演算(deferred operations)の列(この場合は乗算の列)を作る時に起きる. 収縮は演算が実際に実行される時に起きる. 遅延演算の列で特徴づけられる, この形のプロセスを 再帰的プロセス(recursive process)という. このプロセスの実行には, 解釈系は後に実行する演算を覚えている必要がある. n!の計算では, 遅延乗算の列の長さ, 従ってそれを覚えておくのに必要な情報の量は, ステップ数のように, nに線形に(nに比例して)成長する. こういうプロセスを 線形再帰的プロセス(linear recursive process)という.

    これと対照的に, 第二のプロセスは伸び縮みしない. 各ステップで, 任意のnに対して覚えておくのは変数product, counter, max-countの現在の値である. これを 反復的プロセス(iterative process)という. 一般に反復的プロセスの状態は, その状態が一定個数の状態変数(state variables)と, 状態が移った時, 状態変数をどう更新するかの一定した規則と, (場合によっては)プロセスを停止させる条件を規定する終了テストで総括出来る. n!の計算には, 必要なステップ数はnに線形に成長するが, そういうプロセスを 線形反復的プロセス(linear iterative process)という.

    二つのプロセスの違いは別の見方も出来る. 反復の方ではどの時点においてもプログラム変数がプロセスの状態の完全な記述を持っている. 計算をステップの途中で止めたら, 計算再開に必要なのは三つのプログラム変数だけだ. 再帰的プロセスではそうはならない. こちらでは解釈系が保持し, プログラム変数に含まれない「隠れた」情報があり, それが遅延演算の列での「プロセスのいる場所」を示している. 列が長くなると多くの情報を保持しなければならなくなる.30

    反復と再帰を比べる場合, 再帰的プロセス(process)と再帰的手続き(procedure)を混同しないよう注意しなければならない. 手続きが再帰的という時, 手続き定義が(直接にしろ間接にしろ)その手続き自身を指す構文上の事実をいう. しかしプロセスが, 例えば線形再帰のパターンに従うという時, プロセスがどう進化するかをいうので, 手続きの書いてある構文をいうのではない. fact-iterのような再帰的手続きが反復的プロセスを生成するというのは紛わしい. しかしプロセスは実に反復的だ: その状態は三つの変数で完全に維持され, 解釈系はプロセスを実行するのに, 三つの変数を覚えておくだけでよい.

    プロセスと手続きの区別が紛わしい理由の一つは, (Ada, Pascal, Cを含む)通常の言語の実装が, 再帰手続きの実行で消費する記憶量が, プロセスは原理的に反復的であっても, 手続き呼出しの数とともに増加するように設計してあるからである. 従ってこれらの言語では, 反復プロセスはdo, repeat, until, forやwhileのような, 特殊目的の 「ループ構造」に頼ってしか記述出来ない. 5章で検討するSchemeの実装にはこの欠点はない. 反復的プロセスは再帰的手続きとして記述してあっても, 固定スペースで実行出来る. この性質の実装を 末尾再帰的(tail recursive)という. 末尾再帰的な実装では, 反復は通常の手続き呼出し機構で実現出来, 特殊な反復構造は 構文シュガーとしてだけ有用である.31

問題 1.9

次の二つの手続きはどちらも, 引数を1増やす手続きincと, 引数を1減らす手続きdecを使って, 二つの正の整数を足す方法を定義している. 

(define (+ a b)
  (if (= a 0)
      b
      (inc (+ (dec a) b))))

(define (+ a b)
  (if (= a 0)
      b
      (+ (dec a) (inc b))))
置換えモデルを使い, それぞれの手続きが(+ 4 5)を評価する時に生成するプロセスを示せ. そのプロセスは反復的か再帰的か.

問題 1.10

次の手続きはAckermann関数という数学関数を計算する. 
(define (A x y)
  (cond ((= y 0) 0)
        ((= x 0) (* 2 y))
        ((= y 1) 2)
        (else (A (- x 1)
                 (A x (- y 1))))))
次の式の値は何か. 
(A 1 10)

(A 2 4)

(A 3 3)
Aを上で定義した手続きとして, 次の手続きを考える. 
(define (f n) (A 0 n))

(define (g n) (A 1 n))

(define (h n) (A 2 n))

(define (k n) (* 5 n n))
正の整数nに対して手続きf, gおよびhが計算する関数の簡潔な数学的定義を述べよ. 例えば(k n)は5n2を計算する.


29 実際のプログラムでは, fact-iterの定義を隠すため, 前の章で紹介したブロック構造を使うことになろう.
(define (factorial n)
   (define (iter product counter)
     (if (> counter n)
           product
           (iter (* counter product)
                    (+ counter 1))))
   (iter 1 1))
こうしなかったのは, 一度に考えることを出来るだけ少くしたかったからである.

30 5章のレジスタ計算機での手続きの実装を論じる時, 反復的プロセスは, 一定個数のレジスタがあり, 補助記憶はいらない計算機としての「ハードウエア」で実現出来ることを知る. これに対し, 再帰的プロセスの実装は スタック(stack)という補助のデータ構造を使う計算機を必要とする.

31 末尾再帰は長い間翻訳系の最適化手法と思われていた. 末尾再帰の意味の基礎はCarl Hewitt(1977)が与えた. 彼はそれを計算の 「メッセージパッシングモデル」(3章で勉強する)で説明した. これに刺激され, Gerald Jay SussmanとGuy Lewis Steele Jr.はSchemeの末尾再帰的な解釈系を作成した(Steele 1975参照). その後Steeleは末尾再帰が手続き呼出しを翻訳する自然な結果であることを示した(Steele 1977). SchemeのIEEE規格はSchemeの実装が 末尾再帰的であることを求めている.

[ 目次, 前節, 次節, 索引 ]