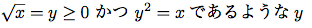
のように定義出来る. これは完全に正当な数学の関数を述べている. これを使うと, ある数がもう一つの数の平方根であるかどうかを調べ, また一般的に平方根に関する事実を導くことが出来る. 一方, この定義は手続きを述べてはいない. 与えられた数の平方根をどう見つけたらよいかについて殆んど何もいっていない. この定義をLisp風にいい替えても役にたたない.
例えば平方根を計算する問題を考えよう. 平方根の関数を
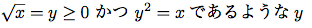
のように定義出来る. これは完全に正当な数学の関数を述べている. これを使うと, ある数がもう一つの数の平方根であるかどうかを調べ, また一般的に平方根に関する事実を導くことが出来る. 一方, この定義は手続きを述べてはいない. 与えられた数の平方根をどう見つけたらよいかについて殆んど何もいっていない. この定義をLisp風にいい替えても役にたたない.
(define (sqrt x)
(the y (and (>= y 0)
(= (square y) x))))
これでは何も解決しない.
関数と手続きの対照は, もののあり様の記述と, ことのなし方の記述の違いの反映である. あるいは, よくいわれるように, 平叙文的知識と命令文的知識の違いである. われわれは数学では通常平叙文的(何である)記述に関心を持つが, 一方, 計算機科学では命令文的(どうする)記述に関心を持つ.20
平方根はどう計算するか. 通常は次々と近似をとるNewton法を使う. 数xの平方根の値の予測値yがあれば, yとx/yの平均値をとるという単純な計算で, 更によい(真の平方根に近い)予測値が得られる.21
例えば2の平方根を次のように計算する. 最初の予測値を1としよう:

この手順を続けると平方根のますますよい近似が得られる.
ではこの手順を手続きを使って形式化しよう. 被開平数(これからその平方根をとろうとする数)の値と予測値の値から出発する. 予測値がわれわれの目的に十分なら終る; そうでなければ改善された予測値を使って手順を繰り返さなければならない. この基本戦略を手続きとして書こう:
(define (sqrt-iter guess x)
(if (good-enough? guess x)
guess
(sqrt-iter (improve guess x)
x)))
予測値はそれと被開平数の前の予測値による商との平均値で改善される:
(define (improve guess x) (average guess (/ x guess)))ただし
(define (average x y) (/ (+ x y) 2))われわれはまた「十分よい」の意味も述べなければならない. 次のが見本になろうが, そうよいテストではない. (問題1.7参照) 考え方は, その二乗と被開平数の差が, 前もって決めた許容値(ここでは0.001)より小さくなるまで答を改善するというのである:22
(define (good-enough? guess x) (< (abs (- (square guess) x)) 0.001))最後に始め方がいる. 例えば常に, どんな数の平方根も1であると予測することが出来る.23
(define (sqrt x) (sqrt-iter 1.0 x))以上の定義を解釈系に入力すれば, sqrtを通常の手続きのように使える.
(sqrt 9) 3.00009155413138 (sqrt (+ 100 37)) 11.704699917758145 (sqrt (+ (sqrt 2) (sqrt 3))) 1.7739279023207892 (square (sqrt 1000)) 1000.000369924366
sqrtのプログラムは, ここまでに紹介した単純な手続き言語でも, 例えばCやPascalで書ける数値計算のプログラムを書くのに十分なことを示した. この言語に, 計算機に何かを何回も実行させる反復
(ループ)構文がないことを考えると, これは驚きである. 一方,
sqrt-iterは, 通常の手続き呼出しの機能があれば, 特別な構文がなくても反復が実行出来ることを示した.24
問題 1.6
Alyssa P. Hackerはifが特殊形式である理由が分らない. 「cond
を利用し, 普通の手続きとして定義してはいけないの?」と聞いた. Alyssaの友人のEva Lu Atorはそうすることはもちろん出来るといって, ifの新版を定義した:
(define (new-if predicate then-clause else-clause)
(cond (predicate then-clause)
(else else-clause)))
EvaはAlyssaにプログラムを見せた:
(new-if (= 2 3) 0 5) 5 (new-if (= 1 1) 0 5) 0Alyssaは喜び, 平方根のプログラムを書き直すのにnew-ifを使った:
(define (sqrt-iter guess x)
(new-if (good-enough? guess x)
guess
(sqrt-iter (improve guess x)
x)))
Alyssaが平方根を計算するのにこれを使おうとすると, 何が起きるか, 説明せよ.
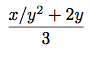
20
平叙文的記述と命令文的記述は, 数学と計算機科学のように, 密接に関係している. 例えばプログラムの出した答が
「正しい」というのは, プログラムについての平叙文的声明である.
プログラムが正しいということを証明する技術を確立しようとした膨大な研究があり, この問題の技術的な困難の多くは, (それでプログラムが作られている)命令文的声明と(ことを簡約化するのに使われる)平叙文的声明の間の変換を取り決めるところにあった. この系統の, プログラム言語設計の最近の主要な分野は, それにより平叙文的声明を使ってプログラムをしようとする,
いわゆる超高レベル言語の探索である. その考え方は, 解釈系を十分技巧的にし, プログラムが指定した「何である」の知識があれば, 自動的に「どうする」の知識が生成出来るようにしようというのである. これは一般的には出来ないが,
進展の見えた重要な領域もある. 4章でこの考え方を再訪しよう.
21
この平方根のアルゴリズムは実は方程式の根を求める一般的技法, Newton法の特別な場合である. 平方根アルゴリズム自身は, 一世紀に
アレキサンドリアのHeronが開発した. 一般的Newton法のLisp手続きとしての表し方を1.3.4章で見ることにしよう.
22
述語には, それが述語であることを覚えておけるように, 疑問符で終る名前をつけることにする. これは表記上の便法である. 解釈系に関する限り, 疑問符は単なる通常の文字である.
23
最初の予測値を1ではなく, 1.0と表したことに注意しよう.
多くのLispの実装では, あまり違いはないが, MITのSchemeでは, 正確な整数と小数は区別し, 二つの整数の除算は小数ではなく, 有理数を作る. 例えば10
を6で割ると5/3になるが, 10.0を6.0で割ると1.6666666666666667になる. (有理数の算術演算をどう実装するかは2.1.1節で学ぶ.) 平方根のプログラムで最初の予測値を1で始め, $x$が正確な整数であれば, その後の平方根計算で出てくる値は小数ではなく, 有理数になる. 有理数と小数の混合演算は小数になる.
そこで, 最初の予測値を1.0から始めると, その後の値は小数にされる.
24
反復を実装するのに, 手続き呼出しを使う場合の効率問題が気になる読者は, 1.2.1節の「末尾再帰」の説明に注意して欲しい.