[ 目次, 前節, 次節, 索引 ]

    平方根を計算する問題は, 予測値が十分良好であるとはどうして分るか, 予測値はどう改善するかなどの, 一連の部分問題に自然に分割出来た. これらの仕事はそれぞれの手続きで実現出来た. sqrtプログラム全体は(図1.2のように)手続きの束と見ることが出来, その束は問題の部分問題への分割を反映している.

図1.2　sqrtプログラムの手続き分解

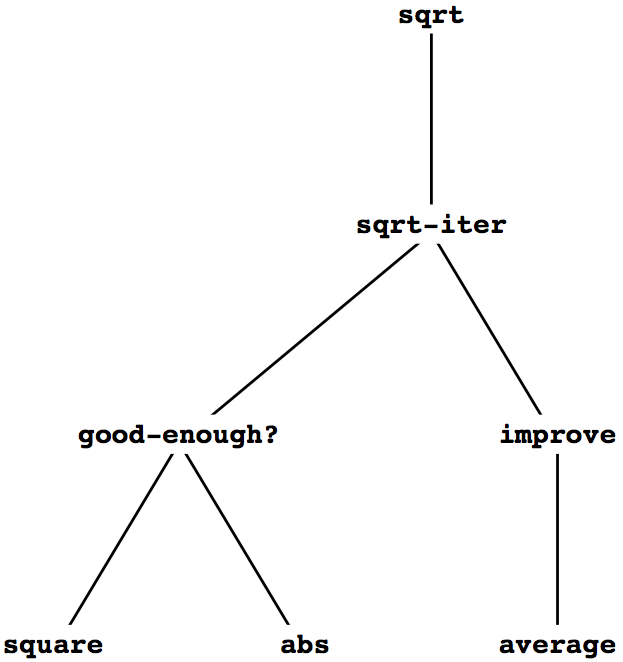
    分割戦略は単にプログラムを部分に分けることより重要である. 大きなプログラムがあれば, 最初の10行, 次の10行, 次の10行のように分けることは出来る. そうではなく, 各手続きは, 他の手続きを定義する時, その部品として使え, まとまった仕事が出来ることが重要だ. 例えば, squareを使ってgood-enough?手続きを定義する時, われわれはsquare手続きを 「ブラックボックス」と見ることが出来る. その時, その手続きがどう 結果を計算するかには関心を持たない. 関心があるのはそれが二乗を計算するという事実だけである. 二乗を計算する方法は隠しておき, 後で考える. 実際good-enough?手続きに関する限り, squareは手続きでなく, 手続きの抽象, いわゆる 手続き抽象(procedural abstraction)である. この抽象のレベルでは, 二乗を計算する手続きならどれでも同じく有用である.

    返す値だけを考えれば, 二乗を計算する次の二つの手続きは区別出来ない. どちらも数の引数をとり, その数の二乗を値として作る.25

(define (square x) (* x x))

(define (square x) 
  (exp (double (log x))))

(define (double x) (+ x x))

    このように手続き定義は細部を隠すことが出来る. 手続きの利用者は, 手続き自身を書かずに, 他のプログラマからブラックボックスとして貰ってくればよい. 利用者はそれを使うためにも, 手続きがどう実装してあるか知らなくてよい.

局所名

(define (square x) (* x x))

(define (square y) (* y y))

(define (good-enough? guess x)
  (< (abs (- (square guess) x)) 0.001))

    パラメタがそれぞれの手続き本体に局所的でないなら, squareのパラメタはgood-enough?のxと混同され, good-enough?の行動はsquareのどの版を使ったかに依存するであろう. つまり, squareは望んだようなブラックボックスではない.

    手続きの仮パラメタには, 手続き定義の中で, 仮パラメタがどんな名前を持っていても構わないという, 特別な役目がある. そういう名前を 束縛変数(bound variable)といい, 手続き定義は仮パラメタを 束縛する(bind)という. 定義の中で束縛変数名を統一的につけ替えても, 手続き定義の意味は変らない.26 変数が束縛されていなければ, 自由である(free)という. 名前が束縛されている式の範囲を 有効範囲(scope)という. 手続き定義の中では, その手続きの仮パラメタとして宣言された束縛変数の有効範囲は, その手続きの本体である.

    上のgood-enough?の定義では, guessとxは束縛変数だが, <, -, abs, squareは自由である. good-enough?の意味はguessやxについては, <, -, abs, squareとは異る名前である限り, どんな名前を選ぼうと変らない. (guessをabsにつけ替えれば, 変数absを 捕捉した(capture)ことの虫となる. absは自由変数から束縛変数に変る.) 一方, good-enough?の意味は自由変数の名前と無関係ではない. 意味は記号absは数の絶対値を計算する手続きの名前であるという, (この定義の外の)事実に依存している. 定義の中でabsをcosに置き換えたら, good-enough?は別の関数を求めることになる.

内部定義とブロック構造

(define (sqrt x)
  (sqrt-iter 1.0 x))

(define (sqrt-iter guess x)
  (if (good-enough? guess x)
      guess
      (sqrt-iter (improve guess x) x)))

(define (good-enough? guess x)
  (< (abs (- (square guess) x)) 0.001))

(define (improve guess x)
  (average guess (/ x guess)))

    このプログラムの問題はsqrtの利用者にとり, 唯一重要な手続きは sqrtだということである. それ以外(sqrt-iter, good-enough? とimprove)は, 利用者の心に虚しく響くだけである. 彼らはsqrt がgood-enough?という手続きを必要としたから, sqrtと一緒に働く他のプログラムの一部にgood-enough?という名前の別の手続きを定義することは出来ない. この問題は大勢のプログラマで巨大なシステムを構築する時, 厳しくなる. 例えば数値計算手続きの大きいライブラリの構築で, 多くの数値関数を逐次近似で計算し, そしてgood-enough?とかimprove という補助手続きを持つかも知れない. 下請け手続きを局所化したい, つまりそれらをsqrtの中に隠し, sqrtがそれぞれ自分の good-enough?手続きを持つ他の逐次近似手続きと共存出来るようにしたい. これを可能とするため, 手続きはその手続きに局所的な 内部定義が出来るようにする. 例えば平方根の問題で

(define (sqrt x)
  (define (good-enough? guess x)
    (< (abs (- (square guess) x)) 0.001))
  (define (improve guess x)
    (average guess (/ x guess)))
  (define (sqrt-iter guess x)
    (if (good-enough? guess x)
        guess
        (sqrt-iter (improve guess x) x)))
  (sqrt-iter 1.0 x))

    このような定義の入れ子をブロック構造(block structure)といい, 最も単純な名前保護の基本的な機構である. しかしもっとよい考えがある. 補助手続きの定義を内部化する他, それらを単純化出来る. xはsqrtの定義に束縛されているから, sqrtの内部で定義する good-enough?, improveおよびsqrt-iterの手続きはxの有効範囲内にある. つまりxをこれらの手続きに明示的に渡す必要はない. そうではなく次のようにxを内部定義で 自由変数にする. そうすればxは外側の手続きsqrtが呼び出された時の引数から値をとる. このやり方を 静的有効範囲(lexical scoping)という.27

(define (sqrt x)
  (define (good-enough? guess)
    (< (abs (- (square guess) x)) 0.001))
  (define (improve guess)
    (average guess (/ x guess)))
  (define (sqrt-iter guess)
    (if (good-enough? guess)
        guess
        (sqrt-iter (improve guess))))
  (sqrt-iter 1.0))

    われわれはブロック構造を出来るだけ使い, 巨大問題を, 扱える部品に分割しよう.28 ブロック構造はプログラム言語 Algol 60で始り, 先進的プログラム言語の殆んどに見られ, 巨大プログラムの構築作業を援助する重要な道具になっている.

25 これらの手続きのうち, どれが効率がよい実装かは, 明らかでない. 使っている計算機に依存する. 「自明な」実装の方が効率の悪い計算機さえある. 対数と真数の大きな表を効率よく記憶している計算機を考えてみよう.

26 名前の統一的つけ替えは実際は曖昧で, 形式的な定義は難しい. 有名な論理学者でも, この点で驚くような過ちをしたことがある.

27 静的有効範囲は手続き中の自由変数は, 外側の定義の束縛を指すようにする; つまり, 手続きが定義された環境を探していく. その詳細は, 環境と解釈系の振舞いを詳しく見た後, 3章で述べよう.

28 組み込まれた定義は 手続き本体の先頭になければならない. 定義と使用をとりまぜたプログラムの実行結果に管理プログラムは責任を負わない.

[ 目次, 前節, 次節, 索引 ]