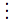(⟨pn⟩ ⟨en⟩))
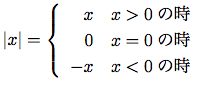
(define (abs x)
(cond ((> x 0) x)
((= x 0) 0)
((< x 0) (- x))))
条件式の一般形は
(cond (⟨p1⟩ ⟨e1⟩)
(⟨p2⟩ ⟨e2⟩)
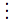(⟨pn⟩ ⟨en⟩))
のように記号condにつづけて,
節(clauses)という
かっこに入った式の対(⟨p⟩ ⟨e⟩)を並べたものである. 対の最初の式は
述語(predicate)---値を真か偽と解釈する式---である.17
条件式は次のように評価する. まず述語⟨p1⟩を評価する. その値が偽なら, ⟨p2⟩を評価する. ⟨p2⟩の値もまた偽なら, ⟨p3⟩を評価する. その手順を値が真である述語が見つかるまで続ける. 見つけたら, 解釈系は, その節の対応する 帰結式(consequent expression)⟨e⟩の値をこの条件式の値として返す. どの⟨p⟩も真でなければ, condの値は定義しない.
述語(predicate)という用語は, 真と偽に評価される式と同様, 真か偽を返す手続きにも使う. 絶対値の手続きabsは基本的手続き <, >と=を使う.18 これらは引数として二つの数をとり, それぞれ第一の数が第二の数より小さい, より大きい, または, に等しいかテストし, その結果に従って真か偽を返す.
絶対値の手続きを書くもう一つの方法は
(define (abs x)
(cond ((< x 0) (- x))
(else x)))
で, 自然言語で「xが0より小さければ-xを返す; それ以外はxを返す」と読むことが出来る.
elseはcondの最後の節で⟨p⟩の代りに書くことが出来る特殊記号である. これは先立つすべての節が通過された時, 対応する⟨e⟩の値をcondにその値として返させる. 実際, 常に真に評価される式はこの⟨p⟩として使える.
絶対値を書く更に別の方法がある:
(define (abs x)
(if (< x 0)
(- x)
x))
これは特殊形式
ifを使う. ifは
場合分けが丁度二つであるような制限つき条件式である. if式の一般形は(if ⟨predicate⟩ ⟨consequent⟩ ⟨alternative⟩)である. if式を評価するには, 解釈系は式の 述語⟨predicate⟩部分を評価する. ⟨predicate⟩の評価の結果が真なら, 解釈系は 帰結部⟨consequent⟩を評価しその値を返す. そうでなければ, 代替部⟨alternative⟩を評価し, その値を返す.19
<, >や=のような基本的述語の他に, 合成述語を作るための論理合成演算がある. 最もよく使われるのが三つある:
• (and ⟨e1⟩ ... ⟨en⟩)
解釈系は式⟨e⟩を左から右へ一つずつ評価する. ある⟨e⟩の評価の結果が偽なら, and式の値は偽で, 残りの⟨e⟩は評価しない. すべての⟨e⟩が真に評価されれば, and式の値は最後の式の値である.
• (or ⟨e1⟩ ... ⟨en⟩)
解釈系は式⟨e⟩を左から右へ一つずつ評価する. ある⟨e⟩の評価の結果が真なら, その値をor式の値として返し, 残りの⟨e⟩は評価しない.
すべての⟨e⟩が偽に評価されれば, or式の値は偽である.
• (not ⟨e⟩)
not式の値は, 式⟨e⟩の評価の結果が偽なら真, そうでなければ偽である.
andとorは, 部分式が必ずしもすべて評価されるのではないから,
手続きではなく, 特殊形式である. notは通常の手続きである.
これらの使用例として, 数xが範囲 5 < x < 10にあるという条件は
(and (> x 5) (< x 10))と書ける. 別の例で, ある数がもう一つの数より大きいか, 等しいかを調べる手続きが定義出来る.
(define (>= x y) (or (> x y) (= x y)))あるいは
(define (>= x y) (not (< x y)))
10
(+ 5 3 4)
(- 9 1)
(/ 6 2)
(+ (* 2 4) (- 4 6))
(define a 3)
(define b (+ a 1))
(+ a b (* a b))
(= a b)
(if (and (> b a) (< b (* a b)))
b
a)
(cond ((= a 4) 6)
((= b 4) (+ 6 7 a))
(else 25))
(+ 2 (if (> b a) b a))
(* (cond ((> a b) a)
((< a b) b)
(else -1))
(+ a 1))
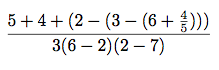
(define (a-plus-abs-b a b) ((if (> b 0) + -) a b))
(define (p) (p))
(define (test x y)
(if (= x 0)
0
y))
彼は次に式(test 0 (p))を評価してみた. 作用的順序の評価を使う解釈系で, Benはどういう振舞いを見るか. 正規順序の評価を使う解釈系で, 彼はどういう振舞いを見るか. 説明せよ. (特殊形式ifの評価規則は, 解釈系が正規順序と作用的順序のどちらを使うかに無関係に同じとする: 述語式を最初に評価し, その結果が帰結式と代替式のいずれを評価するかを決める.)
17
「真か偽と解釈する」とは次の意味である. Schemeでは定数#tと#fで表す特別な二つの値がある. 解釈系が述語の値を調べる時,
#fを偽と解釈する. 他の値は真として扱う. (従って#tは論理的には不要だが,
便利でもある.) 本書では, それぞれ値#tと#fに対応づけられた名前trueとfalseを使おう.
18
absは
「引く」演算子-を使う. これは(- x)のように単項の被演算子と使うと符号反転を表す.
19
ifとcondの違いは, condの節⟨e⟩は式の並びでよいことである. 対応する⟨p⟩が真であれば, ⟨e⟩は順に評価され, 最後の式の値がcondの値として返される. しかしif式では, 帰結部と代替部は単一の式でなければならない.