[ 目次, 前節, 次節, 索引 ]

(define (factorial n)
  (if (= n 1)
      1
      (* (factorial (- n 1)) n)))

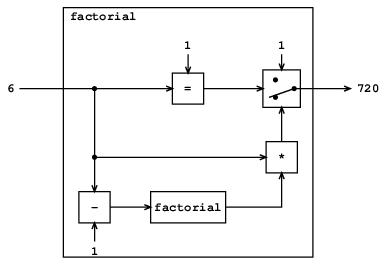
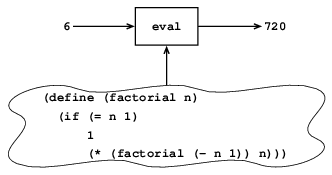
   同様に評価器を機械の記述を入力としてとる, 非常に特別な機械として見ることが出来る. この入力が与えられると, 評価器は記述された機械をエミュレートするように自分を構成する. 例えば図4.3に示すように, 評価器にfactorialの定義を食べさせたとすると, 評価器は階乗が計算出来るようになる.

   この観点から, われわれの評価器は万能機械(universal machine)と見てよい. それは他の機械がLispプログラムとして記述してあれば, それらを真似することが出来る.19 これは衝撃的である. 電気回路の類似の評価器を思い起こそう. これはフィルタのようなある他の回路の設計をコード化した信号を入力としてとる回路である. その入力が与えられたら, 回路評価器は同じ記述のフィルタとして振舞うであろう. そういう万能電気回路は殆んど想像出来ないくらい複雑である. プログラム評価器がかなり単純なプログラムであるのは注意すべきことである.20

   評価器のもう一つの衝撃的な点は, それがプログラム言語で操作されるデータオブジェクトと, プログラム言語自身の間の橋として働くことである. (Lispで実装した)評価器のプログラムが走っていて, 利用者が評価器に式を入力し, 結果を見ているとしよう. 利用者の視点からは, (* x x)のような入力の式は, 評価器が実行すべきプログラム言語での式である. 評価器の視点からは, しかしこの式は正しく定義された規則の集りに従って操作される, 単なるリスト(この場合は*, xとxの三要素のリスト)である.

   利用者のプログラムが, 評価器のデータであることは必ずしも混乱の元ではない. 実際,この区別を無視し, プログラムの中でevalが使えるようにし, 利用者にデータオブジェクトをLispの式として, 積極的に評価する能力を与えることは便利かもしれない. 多くのLisp方言は式と環境を引数としてとり, その環境で式を評価する基本的 eval手続きを用意している.21 従って

(eval '(* 5 5) user-initial-environment)

(eval (cons '* (list 5 5)) user-initial-environment)

(define (run-forever) (run-forever))

(define (try p)
  (if (halts? p p)
      (run-forever)
      'halted))

19 機械がLispで記述されている事実は本質的ではない. われわれの評価器に何か他の言語, 例えばCの評価器として振舞うLispプログラムを与えると, Lisp評価器はC評価器をエミュレートするであろう. それはまたCプログラムとして記述されたどんな機械でもエミュレート出来る. 同様にLisp評価器をCで書くと, Lispプログラムを実行することの出来るC プログラムが作れる. ここでの深い考えは, どんな評価器でも他のものをエミュレート出来るということだ. (必要な時間と記憶の問題は無視して) 「原理的に計算されるもの」の概念は, 言語や計算機とは独立で, それより基盤となる計算可能性(computability)の観念に思い及ぶ. このことは Alan Turing(1912--1954)によって初めて明確に示され, かれの1936年の論文は理論的 計算機科学の基礎を築いた. その論文でTuringは単純な計算モデル---今では Turing機械(Turing machine)として知られている---を提案し, どのような「実効的プロセス」もそういう機械のプログラムとして形式化出来ると論じた. (この議論は Church-Turing定理(Church-Turing thesis)として知られている.) 次にTuringは万能機械, つまりTuring機械のプログラムの評価器として行動するTuring機械を実装した. 彼はこの枠組を使い, Turing機械では計算することの出来ない, 克明に述べられた問題が存在し(問題4.15参照), 従って「実効的なプロセス」として形式化し得ないことを示した. Turingは実質的な計算機科学にも基本的な貢献をした. 例えば彼は 汎用サブルーチンを使ったプログラム構成法を考え出した. Turingの伝記については, Hodges 1983参照.

20 ある人達は比較的単純な手続きで実装された評価器が, 評価器自身より遥かに複雑なプログラムをエミュレート出来るのは, 直観に反するという. 万能評価機械が存在することは, 計算の深遠で驚異的な性質である. 数理論理学の一分野の 再帰理論(recursion theory)は計算の論理的極限を扱う. Douglas Hofstadterの美しい本Gödel, Escher, Bach(1979)はこの話題の幾分かを探求している.

21 警告: この eval基本手続きは, 4.1.3節で作った見本の環境構造ではなく, 実際のScheme環境を使うので, 4.1.1節で実装したeval手続きと同じではない. 実際の環境は利用者が通常のリストとして操作出来るものではない; それにはevalや他の特別な演算によってアクセスされなければならない. 同様に前に見た applyの基本手続きも, 4.1.3と4.1.4節で構成した手続きオブジェクトでなく, 実際のScheme手続きを使うので, 超循環のapplyと同じではない.

22 SchemeのMITの実装には, evalと, 利用者の入力した式が評価される初期環境に束縛された, user-initial-environmentが存在する.

23 halts? は手続きオブジェクトが与えられたとしたが, halts?が手続きの本文と環境にアクセス出来るとしても, この推論は成り立つことに注意しよう. これは, 計算出来ない(non-computable)問題, つまり明白に述べられた仕事で, 計算手順では実行出来ないものの, 明白な例を初めて与えた, Turingの有名な停止問題(Halting Theorem)である.

[ 目次, 前節, 次節, 索引 ]