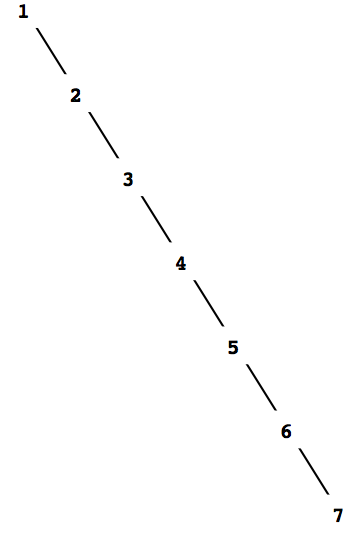
図2.17 1から7までの数を順に追加して出来た極端に不釣合いな木
問題 2.63
下の二つの手続きはそれぞれ二進木をリストに変換する.
簡単にいえば集合は相異るオブジェクトの集りである. もっと精密に定義をするには, データ抽象の方法が使える. つまり集合に使われる演算を規定することで, 「集合」を定義する. それらはunion-set, intersection-set, element-of-set?およびadjoin-setである. element-of-set?は与えられた要素が集合の構成要素であるかという述語である. adjoin-setは引数としてオブジェクトと集合をとり, 元の集合の要素と追加する要素を含む集合を返す. union-setは二つの集合の和集合, つまりどちらかの集合に現れる要素を含んでいる集合を計算する. intersection-setは二つの集合の積集合, つまり両方の集合に現れる要素だけを含む集合を計算する. データ抽象の観点から, 上の解釈と整合していれば, これらの演算を実装するどのような表現を設計するも自由である.37
(define (element-of-set? x set)
(cond ((null? set) false)
((equal? x (car set)) true)
(else (element-of-set? x (cdr set)))))
これを使えばadjoin-setが書ける. 追加すべきオブジェクトが既に集合の中にあれば, 単にその集合を返す. そうでなければ, 集合を表現するリストにオブジェクトを加えるのにconsが使える:
(define (adjoin-set x set)
(if (element-of-set? x set)
set
(cons x set)))
intersection-setには再帰的戦略が使える. set2と, set1のcdrの積集合の作り方が分っていれば, これにset1のcarを加えるかどうかを決めるだけだ. これは(car set1)がset2にもあるかどうかによる. 結果の手続きはこうだ:
(define (intersection-set set1 set2)
(cond ((or (null? set1) (null? set2)) '())
((element-of-set? (car set1) set2)
(cons (car set1)
(intersection-set (cdr set1) set2)))
(else (intersection-set (cdr set1) set2))))
表現の設計で気をつけるべき点は, 効率である. われわれの集合演算に必要なステップ数を考えよう. どれもelement-of-set?を使うから, この手続きのスピードは集合の実装全体の効率に大きく影響する. あるオブジェクトが集合の要素かどうか調べるのに, element-of-set?は全集合を走査しなければならない. (最悪の場合はオブジェクトが集合の中になかったことが分る.) そこで集合の要素数をnとすれば, element-of-set?はn
ステップかかる. だから必要なステップ数はΘ(n)で増加する. この演算を利用するadjoin-setが必要なステップ数もΘ(n)で増加する.
intersection-setは, set1の各要素について,
element-of-set? 検査をするので, 必要なステップ数は関与する集合の大きさの積に従って, つまり大きさnの二つの集合ではΘ(n2)で増加する. union-setについても同様である.
問題 2.59
集合の順序づけられないリスト表現で
union-set演算を実装せよ.
問題 2.60
集合を重複のないリストで表現しようとしてきた. 重複が許されるとしよう. 例えば集合{1, 2, 3}はリスト(2 3 2 1 3 2 2)で表現されるかも知れない. この表現を操作する手続き, element-of-set?,
adjoin-set, union-setおよびintersection-setを設計せよ.
重複なし表現の対応する手続きと比べて効率はどうなるか. 重複なし表現よりこの表現の方が使いたくなる応用はあるだろうか.
順序づけの利点はelement-of-set?に現れる: あるものの存在を調べるのに, もはや全集合を走査することはない. 探しているものより大きい集合の要素にいき当ったら, それは集合の中にないことが分かる:
(define (element-of-set? x set)
(cond ((null? set) false)
((= x (car set)) true)
((< x (car set)) false)
(else (element-of-set? x (cdr set)))))
どのくらいのステップが節約出来ただろう. 最悪の場合, 探しているものは集合の最大の要素かも知れず, ステップ数は順序づけられてない表現と同じである. ところが, 異る大きさのものを探す場合は, ある時はリストの先頭に近い場所で探索を止めることが出来, またある時はリストの大部分を調べなければならないと考えられる. 平均すると集合の半分のものを調べなければならないと考えられる. 従って必要なステップ数の平均は, 約n/2である. これはやはりΘ(n)の増加だが, 前の表現に比べ, ステップ数は平均で2倍の改善になっている.
intersection-setでは更に目覚しい加速が出来る. 順序づけられない表現では, set1の各要素に対し, set2の完全走査を行ったので, この演算はΘ(n2)ステップを必要とした. しかし順序づけられた表現では,もっと巧妙な方法が使える. 二つの集合の最初の要素x1とx2の比較から始める. x1がx2に等しければ, 積集合の要素になる. 積集合の残りは二つの集合のcdrの積集合である. しかしx1がx2より小さいとしよう. x2はset2の最小要素だから, x1 はset2には現れないと結論出来, 積集合には入らない. そこで積集合はset2と, set1のcdrの積集合に等しい. 同様にx2がx1より小さければ, 積集合はset1と, set2のcdrの積集合となる. そこで手続きはこうだ:
(define (intersection-set set1 set2)
(if (or (null? set1) (null? set2))
'()
(let ((x1 (car set1)) (x2 (car set2)))
(cond ((= x1 x2)
(cons x1
(intersection-set (cdr set1)
(cdr set2))))
((< x1 x2)
(intersection-set (cdr set1) set2))
((< x2 x1)
(intersection-set set1 (cdr set2)))))))
このプロセスに必要なステップ数を見積るには, 各ステップで積集合の問題を---
set1かset2のどちらかの最初の要素か, 両方の最初の要素を除去して---より小さい集合の積の計算の問題に引き下げていることに注意しよう.
従って必要なステップ数は, 順序づけられない表現では, サイズの積であったが, 高々set1とset2のサイズの和である. Θ(n2)ではなくΘ(n)の増加であり, 手頃なサイズの集合にとっても, かなりの加速である.
木構造表現の利点はこうだ: 数xが集合に含まれているか調べたいとしよう. xを最上の節の見出しと比べる. xがこれより小さければ, 左部分木だけ探せばよい; xが大きいと右部分木だけ探す. 木が「釣合って」いれば, これらの部分木のそれぞれは, 元のサイズの約半分である. 従って一ステップでサイズnの木の探索問題を, サイズn/2の探索に引き下げた. 木のサイズは各ステップで半分になるので, サイズnの木の探索に必要なステップ数はΘ(log n)で増加すると考えられる.38 大きい集合では, これは前の表現よりかなりの加速である.
木はリストを使って表現出来る. 各節は三つの項: その節の見出し, 左部分木および右部分木のリストである. 左や右の部分木が空リストなのは, そこには部分木が接続されていないことを示す. この表現を次の手続きで記述する:39
(define (entry tree) (car tree)) (define (left-branch tree) (cadr tree)) (define (right-branch tree) (caddr tree)) (define (make-tree entry left right) (list entry left right))
上に述べた戦略を使い, element-of-set?を書くことが出来る:
(define (element-of-set? x set)
(cond ((null? set) false)
((= x (entry set)) true)
((< x (entry set))
(element-of-set? x (left-branch set)))
((> x (entry set))
(element-of-set? x (right-branch set)))))
集合の追加も同様に実装出来, Θ(log n)ステップが必要である. xを追加するのにxを右の枝に追加するか左の枝に追加するか決めるため, xと節の見出しを比べる. xを然るべき枝に追加すると, この新しい枝を元の見出しともう一方の枝と接続する. xが見出しと同じなら単にその節を返す. xを空リストに追加することになれば, 見出しがxで, 右と左の枝が空の木を生成する. 手続きはこうだ:
(define (adjoin-set x set)
(cond ((null? set) (make-tree x '() '()))
((= x (entry set)) set)
((< x (entry set))
(make-tree (entry set)
(adjoin-set x (left-branch set))
(right-branch set)))
((> x (entry set))
(make-tree (entry set)
(left-branch set)
(adjoin-set x (right-branch set))))))
木の探索が対数的ステップで実行出来るという上の主張は, 木が「釣合っている」つまり各部分木が親の要素のほぼ半分ずつを含むように, それぞれの木の左と右の部分木がほぼ等しい個数の要素を持っているという仮説に基づいている. しかし構成した木が釣合っていると, どうして信じられるだろう. 釣合っている木から出発しても, adjoin-setで要素を追加していくと, 不釣合いなものになるかも知れない. 新しく追加される要素の位置は, 既に集合にあったものとの比較に依存するから, 「ランダムに」要素を追加していくと木は平均として釣合うと期待出来る. しかしこれは保証されない. 例えば空集合から始めて1から7までの数を順に追加すると図2.17に示すように極端に不釣合いな木になってしまう. 左部分木はすべて空で, 単なる順序づけられたリストに対する利点はない. この問題を解決する一つの方法は, 任意の木を同じ要素を持つ釣合った木に変換する演算を定義することである. adjoin-set
演算を数回やる度にこの変換を実行すると, 木を釣合せておくことが出来る. この問題の別の解決法の大部分は, 探索と挿入が共にΘ(log n)ステップで出来る新しいデータ構造を設計することだ.
40

図2.17 1から7までの数を順に追加して出来た極端に不釣合いな木
問題 2.63
下の二つの手続きはそれぞれ二進木をリストに変換する.
(define (tree->list-1 tree)
(if (null? tree)
'()
(append (tree->list-1 (left-branch tree))
(cons (entry tree)
(tree->list-1 (right-branch tree))))))
(define (tree->list-2 tree)
(define (copy-to-list tree result-list)
(if (null? tree)
result-list
(copy-to-list (left-branch tree)
(cons (entry tree)
(copy-to-list (right-branch tree)
result-list)))))
(copy-to-list tree '()))
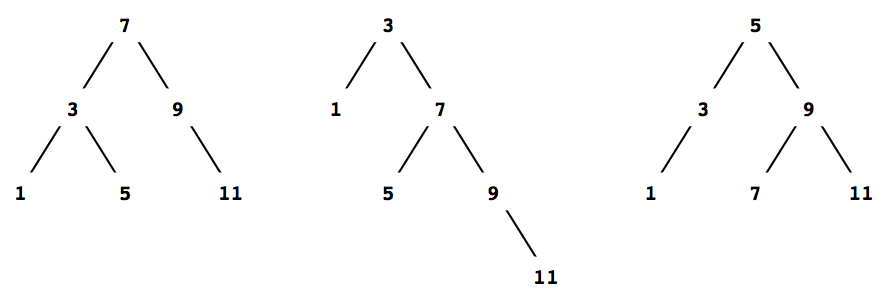
a. 二つの手続きはすべての木に対して同じ結果を生じるか. そうでなければ, 結果はどう違うか. 二つの手続きは図2.16のような木からどういうリストを生じるか.
(define (list->tree elements)
(car (partial-tree elements (length elements))))
(define (partial-tree elts n)
(if (= n 0)
(cons '() elts)
(let ((left-size (quotient (- n 1) 2)))
(let ((left-result (partial-tree elts left-size)))
(let ((left-tree (car left-result))
(non-left-elts (cdr left-result))
(right-size (- n (+ left-size 1))))
(let ((this-entry (car non-left-elts))
(right-result (partial-tree (cdr non-left-elts)
right-size)))
(let ((right-tree (car right-result))
(remaining-elts (cdr right-result)))
(cons (make-tree this-entry left-tree right-tree)
remaining-elts))))))))
a. partial-treeがどう働くか, 出来るだけ明快な短い説明を書け.
list->treeがリスト(1 3 5 7 9 11)に対して作る木を描け. 企業の従業員ファイルや会計システムの取引きのような, 大量の個々の レコードを持つデータベースを考えよう. 通常のデータ管理システムは, レコードの中のデータにアクセスし, 修正するのに膨大な時間を費しているので, レコードにアクセスする効率のよい手段が要求される. これは各レコードの識別 キー(key)として働く部分を見分けることで行う. キーはレコードを一意的に識別する, どのようなものでもよい. 従業員ファイルなら従業員番号であったりする. 会計システムなら取引き番号かも知れない. キーが何であれ, レコードをデータ構造として定義する時, レコードに対応づけられたキーを検索する key選択手続きを用意しなければならない.
データベースをレコードの集合として表現しよう. あるキーのレコードを見つけるのに, 引数としてキーとデータベースをとり, そのキーを持つレコードを返すか, そういうレコードがなければ偽を返す手続きlookupを使う. lookupはelement-of-set?と殆んど同じ方法で実装出来る. 例えばレコード自身が順序づけられないリストで表現されているなら,
(define (lookup given-key set-of-records)
(cond ((null? set-of-records) false)
((equal? given-key (key (car set-of-records)))
(car set-of-records))
(else (lookup given-key (cdr set-of-records)))))
を使うことが出来る.
もちろん大きな集合を表現するには順序づけられないリストよりよい方法はある. 「ランダムにアクセスする」レコードを持つ情報検索システムは通常は前に論じた二進木表現のような木構造に基づいた実装がしてある. そういうシステムを設計する時, データ抽象の技法は大いに役立つ. 設計者は順序づけられないリストのような, 単純直截な表現を使って最初の実装を作り出すことが出来る. しかし長期的なシステムには不向きかも知れないが, システムの他の部分をテストするための「拙速な」データベースを用意するのに有効である. 後になってデータ表現はより精巧なものに修正出来る. データベースが抽象的選択子と構成子を使ってアクセスされるなら, 表現の変更は他の部分の変更を必要としない.
問題 2.66
レコードの集合がキーの数値で順序づけられている二進木で構造化されている場合のlookup手続きを実装せよ.
37
より形式的には「上の解釈と整合していれば」は演算がこのような一群の規則を満しているということである:
• 任意の集合Sと任意のオブジェクトxとについて,
(element-of-set? x (adjoin-set x S)) が真. (平たくいえば「オブジェクトを集合に追加すると, そのオブジェクトを含む集合が出来る.」)
• 任意の集合SとTと任意のオブジェクトxとについて, (element-of-set? x (union-set S T))は(or (element-of-set? x S) (element-of-set? x T))に等価. (平たくいえば「(union-set S T)の要素はSかTにある要素である. 」)
• 任意のオブジェクトxについて(element-of-set? x '())
は偽. (平たくいえば「空集合の要素になるオブジェクトはない.」)
38
問題のサイズをステップ毎に半分にするのは, 1.2.4節の高速べき乗アルゴリズムや, 1.3.3節の区間二分探索法で見たように,
対数的増加の著しい性質である.
39
われわれは集合を木を使って, 木をリストを使って表現しようとしている. 実際データ抽象はデータ抽象の上に構築される. 手続きentry,
left-branch, right-branchおよびmake-treeは「二進木」の抽象を, このような木をリスト構造を使って表現しようと思う特定の表現から隔離する方法と見ることが出来る.
40
そういう構造には
B木(B-tree)とレッドブラック木(red black tree)がある.
この問題を扱ったデータ構造の多くの文献がある.
Cormen,
Leisersonおよび
Rivest 1990参照
41
問題2.63--2.65は
Paul Hilfingerによる.