記号微分プログラムの開発に際し, 2.1.1節の有理数システムの開発の時に採用したデータ抽象と同じ手法を採用しよう. つまりわれわれはまず「和」, 「積」や「変数」のような抽象オブジェクトに, それがどう表現されるかには心配せず, 操作する微分アルゴリズムを定義する. その後で表現の問題に向うことにする.

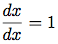
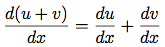
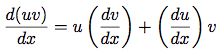
後の二つの規則は本来再帰的であることに注意しよう. つまり和の微分をとるには, まず項の微分を求め, それらを足す. 各項はまた分解が必要な式であるかも知れない. 段々と小さい部分に分解すると, 遂には定数か変数になり, その微分は0か1である.
これらの規則を手続きに組み込むには, 有理数の実装の設計の時のように, 多少の
希望的思考をしなければならない. 代数式を表現する手段があれば, その式が和か積か定数か変数か分る必要がある. 式のその部分を取り出すことが出来なければならない. 例えば和については加数[addend](第一項)と被加数[augend](第二項)が取り出したい. また部品から式が構成出来なければならない. 次の選択子, 構成子と述語を実装した手続きは既にあると仮定しよう:
(variable? e) eは変数か. (same-variable? v1 v2) v1とv2は同じ変数か. (sum? e) eは和か. (addend e) eの加数. (augend e) eの被加数. (make-sum a1 a2) a1とa2の和を構成. (product? e) eは積か. (multiplier e) eの乗数. (multiplicand e) eの被乗数. (make-product m1 m2) m1とm2の積を構成.これらと数を見分ける基本述語 number?を使うと, 次の手続きのように微分規則を表すことが出来る:
(define (deriv exp var)
(cond ((number? exp) 0)
((variable? exp)
(if (same-variable? exp var) 1 0))
((sum? exp)
(make-sum (deriv (addend exp) var)
(deriv (augend exp) var)))
((product? exp)
(make-sum
(make-product (multiplier exp)
(deriv (multiplicand exp) var))
(make-product (deriv (multiplier exp) var)
(multiplicand exp))))
(else
(error "unknown expression type -- DERIV" exp))))
このderiv手続きは完全な微分アルゴリズムを取り込んでいる. これは抽象データを使って表されているので, 正当な選択子と構成子を設計しさえすれば, 代数式の表現をどう選ぶかに無関係に働く. これが次に論ずべき点である.
(define (variable? x) (symbol? x))• 二つの変数はそれを表現している記号がeq?なら同じである:
(define (same-variable? v1 v2) (and (variable? v1) (variable? v2) (eq? v1 v2)))• 和と積はリストとして構成する:
(define (make-sum a1 a2) (list '+ a1 a2)) (define (make-product m1 m2) (list '* m1 m2))• 和は最初の要素が記号+であるリストである:
(define (sum? x) (and (pair? x) (eq? (car x) '+)))• 加数は和のリストの第二項である:
(define (addend s) (cadr s))• 被加数は和のリストの第三項である:
(define (augend s) (caddr s))• 積は最初の要素が記号*であるリストである:
(define (product? x) (and (pair? x) (eq? (car x) '*)))• 乗数は積のリストの第二項である:
(define (multiplier p) (cadr p))• 被乗数は積のリストの第三項である:
(define (multiplicand p) (caddr p))ところで, 動作する微分プログラムにするためには, derivのアルゴリズムとこれらを組み合せればよい. その振舞いの例を見よう.
(deriv '(+ x 3) 'x)
(+ 1 0)
(deriv '(* x y) 'x)
(+ (* x 0) (* 1 y))
(deriv '(* (* x y) (+ x 3)) 'x)
(+ (* (* x y) (+ 1 0))
(* (+ (* x 0) (* 1 y))
(+ x 3)))
このプログラムは正しい答を出す; しかし簡約化はしていない. 確かに
この困難は有理数の実装で出会ったのとよく似ている: 答を最も簡単な形にまで簡約しなかった. 有理数の簡約化を実施するのに, 実装の構成子と選択子だけを変更する必要があった. ここでも似たような戦略をとろう. derivは変更したくない. そうではなく, make-sumを変更し, 両方の被演算子が数値なら, make-sumはそれらを足し, 和を返す. また被演算子の一方が0なら, make-sumはもう一方の被演算子を返す.
(define (make-sum a1 a2)
(cond ((=number? a1 0) a2)
((=number? a2 0) a1)
((and (number? a1) (number? a2)) (+ a1 a2))
(else (list '+ a1 a2))))
これは式が与えられた数に等しいかを見る手続き =number?を使っている:
(define (=number? exp num) (and (number? exp) (= exp num)))同様にmake-productを変更し, 0掛ける何かは0で, 1掛ける何かはそれ自身という規則を組み込もう:
(define (make-product m1 m2)
(cond ((or (=number? m1 0) (=number? m2 0)) 0)
((=number? m1 1) m2)
((=number? m2 1) m1)
((and (number? m1) (number? m2)) (* m1 m2))
(else (list '* m1 m2))))
先ほどの三つの例がどうなるか見よう.
(deriv '(+ x 3) 'x) 1 (deriv '(* x y) 'x) y (deriv '(* (* x y) (+ x 3)) 'x) (+ (* x y) (* y (+ x 3)))これはかなりの改善であるが第三の例は, われわれが「最簡だ」と賛成する形へ式を持っていくプログラムにするには, まだ長い道のりがあることを示している. 代数的単純化の問題は, いろいろな理由のうちでも, ある目的にとって最簡なのが, 他の目的にはそうでないということがあって, 複雑なのである.
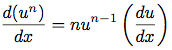
(deriv '(* x y (+ x 3)) 'x)と表現出来る. 和と積の表現だけを変更し, derivの手続きは全く変更せずに試みよ. 例えば和のaddendは第一項, augendは残りの項の和とする.