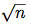に等しいかそれより小さい除数を持つという事実に基づく.44
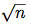つまりアルゴリズムは1との間のテスト用除数だけが必要である. 従ってnが素数かどうか見るのに必要なステップ数は,
Θ(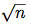)の増加の程度である.
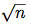)の増加の程度のものと,
Θ(log n)の増加の程度の「確率的」アルゴリズムのものの, 二つの方法を述べる. 節末の問題はこれらのアルゴリズムに基づくプログラミングプロジェクトを提案する.
(define (smallest-divisor n)
(find-divisor n 2))
(define (find-divisor n test-divisor)
(cond ((> (square test-divisor) n) n)
((divides? test-divisor n) test-divisor)
(else (find-divisor n (+ test-divisor 1)))))
(define (divides? a b)
(= (remainder b a) 0))
ある数が素数であることは次のようにして分る: nは, n自身がその最小除数である時に限り, 素数である.
(define (prime? n) (= n (smallest-divisor n)))
find-divisorの終了テストは, nが素数でなければ, 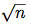に等しいかそれより小さい除数を持つという事実に基づく.44
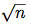つまりアルゴリズムは1との間のテスト用除数だけが必要である. 従ってnが素数かどうか見るのに必要なステップ数は,
Θ(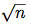)の増加の程度である.
nが素数でない時, 一般にa < nなる殆んどの数について上の関係は成り立たない. このことから次の素数性テストのアルゴリズムが出来る: 与えられた数nに対し, a < nなる ランダムな数のnを法としたanの剰余を計算する. 結果がaでなければ, nは確実に素数ではない. 結果がaなら, nが素数である確率は高い. 別の数aをランダムにとり, 同じようにテストする. また等式が成り立つなら, nが素数であることに更に確信が持てる. 更にいろいろなaの値で確めることで, 結果の確信度が増す. このアルゴリズムはFermatテストとして知られている.
Fermatテストを実装するには, ある数のべき乗の別の数を法とした剰余を計算する手続きがいる:
(define (expmod base exp m)
(cond ((= exp 0) 1)
((even? exp)
(remainder (square (expmod base (/ exp 2) m))
m))
(else
(remainder (* base (expmod base (- exp 1) m))
m))))
これは1.2.4節のfast-exptによく似ている. 逐次平方を使うので, ステップ数は指数に対数的に増加する.46
Fermatテストは数aを1とn - 1の間に, 両端を含めてランダムに選んで実行し, nを法としたaのn乗の剰余がaに等しいかを調べる. 乱数aはSchemeに基本の手続き randomを使って選ぶ. randomは入力の整数より小さい非負の整数を返す. そこで, 1とn - 1の間の乱数を得るには, randomをn - 1で呼び出し, 結果に1を足す.
(define (fermat-test n)
(define (try-it a)
(= (expmod a n n) a))
(try-it (+ 1 (random (- n 1)))))
次の手続きはパラメタで与えられた回数だけテストを実行する. テストに全回成功すると結果として真を返し, そうでなければ偽を返す.
(define (fast-prime? n times)
(cond ((= times 0) true)
((fermat-test n) (fast-prime? n (- times 1)))
(else false)))
困ったことにこの仮定は正しくない. Fermatテストをだます数: 素数でないのに, a < nのすべての整数についてanがnを法としてaに合同になる数が存在する. そういう数はごく稀なので, 実用上Fermatテストは十分信頼出来る.47 だまされないようなFermatテストの変形もある. これらのテストではFermatテストのように, nの素数性を調べるのに, a < nなるランダムな整数を選び, nとaに依存するある条件を検査する. (この種のテストの例は問題1.28参照.) 他方, Fermatテストとは対照的に, 任意のnについて, nが素数でなければ, a < nの殆んどの整数に対し, 条件が成立しないことが証明出来る. nがランダムなaで成功すれば, nが素数である機会は半々より大きい. 二つのランダムなaに対して成功すれば, nが素数である機会は3/4より大きい. 更に多くのランダムに選んだaの値でテストすれば, エラーの確率はいくらでも小さくすることが出来る.
エラーの機会が任意に小さくなることの証明出来るテストの存在は,
確率的アルゴリズム(probabilistic algorithms)として知られるようになり, この種のアルゴリズムへの関心を目覚させた. この領域のかなりの研究活動があり, 確率的アルゴリズムは多くの分野で応用されている.48
{かくりつてき@確率的|)}
問題 1.21
smallest-divisor手続きを使い, 次の数の最小除数を見つけよ: 199,
1999, 19999.
問題 1.22
殆んどのLispの実装には基本手続きruntimeがあり, システムが走った時間を(例えばマイクロ秒で)示す整数を返す. 次のtimed-prime-test手続きは整数nで呼び出されると, nを印字し, nが素数かどうかを調べ,
nが素数なら手続きは三つの星印とテストに要した時間を印字する.
(define (timed-prime-test n)
(newline)
(display n)
(start-prime-test n (runtime)))
(define (start-prime-test n start-time)
(if (prime? n)
(report-prime (- (runtime) start-time))))
(define (report-prime elapsed-time)
(display " *** ")
(display elapsed-time))
この手続きを使い, 指定範囲の連続する奇整数について素数性を調べる手続きsearch-for-primesを書け. その手続きで, それぞれ1,000, 10,000,
100,000, 1,000,000より大きい, 小さい方から三つの素数を見つけよ. 素数をテストする時間に注意せよ. テストのアルゴリズムはΘ(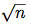)の増加の程度だから, 10,000前後の素数のテストは1,000前後の素数のテストの
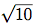倍かかると考えよ. 時間のデータはこれを支持するか. 100,000,
1,000,000のデータは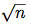予想のとおりだろうか. 結果はプログラムが計算に必要なステップ数に比例した時間で走るという考えに合っているか.
(define (expmod base exp m) (remainder (fast-expt base exp) m))と単純に書ける筈だといった. これは正しいか. これも高速素数テストと同じに使えるか, 説明せよ.
(define (expmod base exp m)
(cond ((= exp 0) 1)
((even? exp)
(remainder (* (expmod base (/ exp 2) m)
(expmod base (/ exp 2) m))
m))
(else
(remainder (* base (expmod base (- exp 1) m))
m))))
「違いが分らん」とLouis, 「分る」とEvaがいった. 「手続きをこのように書き替えたので, Θ(log n)のプロセスをΘ(n)のプロセスにしてしまった.」 説明せよ.
44
dがnの除数なら, n/dも除数である. しかしdとn/dの両者が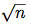より大きいことはない.
45
Pierre de Fermat(1601--1665)は近代整数論の創設者と考えられる. 彼は多くの重要な整数論の結果を得たが, 通常は証明抜きで結果のみ発表した.
Fermatの小定理は, 1640年に書いた手紙の中に述べてある. 最初の公開された証明は1736年,
Eulerによる. (これに先立つ同じ証明は
Leibnizの未発表草稿に発見された.) 最も有名なFermatの結果---Fermatの最終定理といわれる---は, 1637年, (三世紀のギリシャの数学者
Diophantusの){\it Arithmetic}の彼のコピーに, 「実にすばらしい証明を見つけたが, この余白はそれを書くには狭過ぎる」という注記とともに, 書き留められている. Fermatの最終定理の証明を見つけることは, 整数論の最も有名な問題であった. 完全な証明は1995年, プリンストン大学の
Andrew Wilesが与えた.
46
指数eが1より大きい場合の簡約化では, 任意の整数x, yとmについて, x × y modulo mの剰余は,
x modulo mとy modulo mの剰余を別々に計算し, その結果を掛け合せ,
更に積のmodulo mの剰余をとればよいという事実に基づいている. eが偶数の場合は, be/2 modulo mの剰余を計算し, 二乗し, そのmodulo mの剰余をとる. これはmより遥かに大きい数値を扱わずに計算が実行出来, 有用である. (問題1.25と比較せよ)
47
Fermatテストをだます数は,
Carmichael 数(Carmichael numbers)といい, 非常に稀だということ以外はよくわからない. 100,000,000以下のCarmichael数は255個あり, 小さい方のいくつかは561, 1105, 1729, 2465, 2821および6601である. ランダムに選んだ非常に大きい数の素数性のテストで, Fermatテストをだます数に遭遇する確率は,
宇宙線が計算機の「正しい」アルゴリズムに誤りを生じさせる確率より小さい.
アルゴリズムが前の理由から不適切であり, 後の理由からとしないのは,
数学と工学の違いを見せる.
48
確率的アルゴリズムの最も目覚しい応用は,
暗号の分野である. 200桁の数の素因数分解は, いまでも計算的に不可能だが,
そういう数の素数性はFermatテストを使い, 数秒で調べられる. この事実は
Rivest,
Shamirと
Adlemanの提案(1977)による, 「破られない暗号」構成の技術基盤になっている.
RSAアルゴリズム(RSA algorithm)は電子通信の安全性を高める技術として広く使われている. これらの展開により, かつてはそのために研究された「純粋」数学の話題であった
素数研究は, 暗号, 電子取引き, 情報検索への重要で実用的応用が開かれた.