[ 目次, 前節,
次節, 索引 ]
1.2.5 最大公約数
二つの整数aとbの最大公約数(GCD)は, a, bの両方を剰余なしに割り切る最大の整数と定義する. 例えば16と28のGCDは4である. 2章で有理数演算の実装法を検討する時, 有理数を既約にするためGCDを計算する必要がある. (有理数を既約にするには分子と分母をそのGCDで割る. 例えば16/28は4/7に既約する.) 二つの整数のGCDを見つける一つの方法は, それらを素因数分解し, 共通の因子を探すことだが, 遥かに効率的な有名なアルゴリズムがある.
このアルゴリズムは, aをbで割った剰余をrとすると, aとbの公約数はbとrの公約数と全く同じであるという考えによる. つまり
GCD (a,b)= GCD (b,r)
の式を使い, GCDの計算を次々とより小さい数の対のGCDを計算する問題に変えていく. 例えば,
| GCD (206,40) | = GCD (40,6) |
| = GCD (6,4) |
| = GCD (4,2) |
| = GCD (2,0) |
| = 2 |
とGCD(206, 40)をGCD(2, 0), つまり2へ縮小させる. 二つのどのような正の整数から始めても, この簡約化を繰り返すうちに最後は二番目の数が0の対になることが示せる. GCDはその対のもう一つの方の数である. このGCDの計算法はEuclidのアルゴリズム (Euclid's Algorithm)として知られている.42
Euclidのアルゴリズムを手続きに表すのは容易である:
(define (gcd a b)
(if (= b 0)
a
(gcd b (remainder a b))))
これは反復的プロセスを生成し, ステップ数は関与する数に対し対数的に増加する.
Euclidのアルゴリズムが必要とするステップ数が, 対数的に増加するという事実は, Fibonacci数と面白い関係にある.
Laméの定理: Euclidのアルゴリズムである対のGCDの計算にk
ステップが必要なら, 対の小さい方の数はk番目のFibonacci数に等しいかそれより大きい.43
この定理を使うとEuclidのアルゴリズムの増加の程度が見積れる. nを手続きへの二つの入力のうち, 小さい方とする. プロセスがkステップかかるとすれば, n ≥ Fib(k) ≈ φk
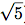 でなければならない. 従ってステップ数kはnの(φを底とする)対数的に増加する. 従って増加の程度はΘ(log n)である.
でなければならない. 従ってステップ数kはnの(φを底とする)対数的に増加する. 従って増加の程度はΘ(log n)である.
問題 1.20
手続きが生成するプロセスはもちろん解釈系が使う規則に依存する. 例えば上で述べた反復的gcd手続きを考え, 1.1.5節で論じた正規順序評価を使って解釈したとする. (ifの正規順序評価規則は問題1.5に書いてある.)
(正規順序の)置換え法を使い, (gcd 206 40)の評価で生成されるプロセスを図示し, 実際に実行されるremainder演算を指示せよ.
(gcd 206 40)の正規順序評価で, remainder演算は実際に何回実行されるか.
作用的順序ではどうか.
42
EuclidのアルゴリズムはEuclidのElements(Book 7. 300 B.C.頃)に現れるのでそういわれる.
Knuth(1973)によれば, 知られていて自明でないアルゴリズムでは最も古い. エジプトの古い乗算法(問題1.18)は更に古いが, Knuthの説明では, Euclidのアルゴリズムは, 例示によらず, 一般的なアルゴリズムとして表現した最も古いものである.
43
この定理は1845年にフランスの数学者で工学者であり,
数理物理学への貢献で知られている
Gabriel Laméが証明した. 定理を証明するにはEuclidのアルゴリズムがk回で終了する対, (ak, bk) (ak ≥ bkとする)を考える. 証明は(ak1, bk+1) → (ak, bk) → (ak-1,
bk-1)が簡約化の連続する三回の対であるとすれば, bk+1 ≥ bk +
bk-1であるという主張に基づく. この主張の証明には, 簡約化のステップが変換ak-1 = bk, bk-1 = (akをbkで割った剰余)と定義されていることに注意する. 第二の式は適当な正の整数qを使い, ak = q bk
+ bk-1ということだ. qは少くても1だから, ak = q bk + bk-1
≥ k + bk-1である. しかし前回の簡約ステップで, bk+1 = ak.
そこでbk+1 = ak ≥ bk + bk-1. 主張は証明出来た. 定理はアルゴリズムが終了するのに必要なステップ数kに関する帰納法で証明する. k
= 1の時, bは少くてもFib(1)=1より大きいことを要求するので, 結論は真.
kに等しいかkより小さいすべての整数につき, 結論が真であると仮定し,
k + 1についての結論を導こう. (ak+1, bk+1) → (ak,
bk) → (ak-1, bk-1)を簡約化プロセスの連続する対とする.
帰納の仮説により, bk-1 ≥ Fib(k - 1)かつbk ≥ Fib(k). 先に証明した主張とFibonacci数の定義から,
bk+1 ≥ bk + bk - 1 ≥ Fib(k) + Fib(k - 1) = Fib(k
+ 1). Laméの定理の証明は終った.
[ 目次, 前節, 次節, 索引 ]
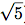 でなければならない. 従ってステップ数kはnの(φを底とする)対数的に増加する. 従って増加の程度はΘ(log n)である.
でなければならない. 従ってステップ数kはnの(φを底とする)対数的に増加する. 従って増加の程度はΘ(log n)である.