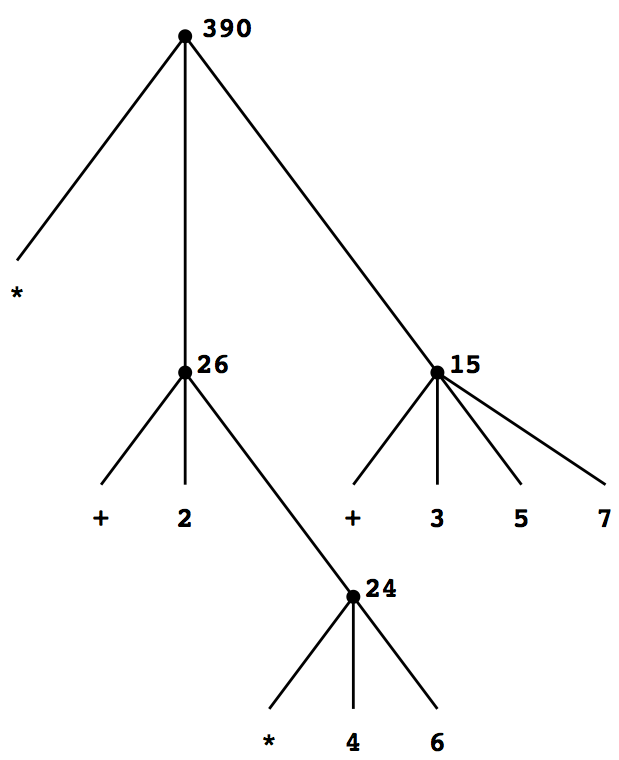
次に, 第一の規則を繰り返し使っていると, 評価する必要のない数字列,基本演算子, またはそれ以外の名前のような, 組合せでない基本的な式の地点へ到る.
基本的な場合を扱うのに次を規定する.
• 数字列の値は, その表す数値とする.
• 基本演算子の値は, 対応する演算を実行する機械命令の列とする.
• それ以外の名前の値は, その環境で名前と対応づけられたオブジェクトとする.
+や*のような記号は大域環境に含まれていて, その「値」である機械命令の列に対応づけられていると規定すれば, 第二の規則は第三の規則の特例と見てもよい. 注意すべきは式での記号の意味の確定における
環境の役割である. Lispのような対話型言語で(+ x 1)のような式の値を云々するのは, 記号x(あるいは記号+)の意味を与える環境のことをいわずば無意味である. 3章で分るように, 環境は評価が行われる文脈を提供するのもだという考えは, プログラムの実行を理解する上で重要な役割を果している.
上の評価規則が定義は扱わないことに注意して欲しい. 例えば, (define x 3) の評価はdefineを二つの引数(一方は記号xの値で, もう一方は3)に作用させるのではない. defineの目的はxを値に対応づけることでしかない. (つまり, (define x 3)は組合せではない.)
このような一般的評価規則の例外を特殊形式(special forms)という. defineはこれまでに現れたただ一つの特殊形式だが, 他のものにもすぐ出会う.
各特殊形式はそれ自身の評価規則を持つ. (それぞれに特有の評価規則のある)
いろいろな種類の式でプログラム言語の
構文規則が出来ている. 他の多くのプログラム言語と比べ, Lispはとても単純な構文規則を持っている; つまり, 式の評価規則は, 単純な一般規則と, 少数の特殊形式に特化した規則で出来ている.11
10
第一段階で評価規則が組合せの最左端の要素を評価すべきだというのは, 現時点ではそこに, 加算や乗算のような組込み基本手続きを表す+や*のような演算子しか来ないことから, おかしいと思うかもしれない. 演算子自体が合成式であるような組合せに使えることが後で分るであろう.
11
一様な形に書けるのに, ただ便利ということで, 別の形をとる表層構文をPeter Landinの作った用語で構文シュガー(syntactic sugar)という. 他の言語の利用者と比べると, Lispのプログラマは概して構文問題を気にしない. (反対にPascalの文法書が, いかに多くを構文記述に使っているか見て欲しい.) この構文無視は, 一つにはそれによって表層構文の変更が簡単になるLispの柔軟さのせいであり, もう一つには, 言語を一様でなくす「便利な」構文構造は, プログラムが巨大で複雑になった時, 必要以上の困難を惹き起すということの認識による.
Alan Perlisは「構文シュガーはセミコロンの癌のもとだ」といった. [コロンは大腸のこと]