�$B&K�(B3.3�$B@a�(B
�$BLdBj�(B 3.12�$B!!�(B
�$BLdBj�(B 3.13�$B!!�(B
�$BLdBj�(B 3.14�$B!!�(B
�$BLdBj�(B 3.15�$B!!�(B
�$BLdBj�(B 3.16�$B!!�(B
�$BLdBj�(B 3.17�$B!!�(B
�$BLdBj�(B 3.18�$B!!�(B
�$BLdBj�(B 3.19�$B!!�(B
�$BLdBj�(B 3.20�$B!!�(B
�$BLdBj�(B 3.21�$B!!�(B
�$BLdBj�(B 3.22�$B!!�(B
�$BLdBj�(B 3.23�$B!!�(B
�$BLdBj�(B 3.24�$B!!�(B
�$BLdBj�(B 3.25�$B!!�(B
�$BLdBj�(B 3.26�$B!!�(B
�$BLdBj�(B 3.27�$B!!�(B
�$BLdBj�(B 3.28�$B!!�(B
�$BLdBj�(B 3.29�$B!!�(B
�$BLdBj�(B 3.30�$B!!�(B
�$BLdBj�(B 3.31�$B!!�(B
�$BLdBj�(B 3.32�$B!!�(B
�$BLdBj�(B 3.33�$B!!�(B
�$BLdBj�(B 3.34�$B!!�(B
�$BLdBj�(B 3.35�$B!!�(B
�$BLdBj�(B 3.36�$B!!�(B
�$BLdBj�(B 3.37�$B!!�(B
�$B2sO)%7%_%e%l!<%?�(B�$B!!�(B
�$B@)Ls%7%9%F%`�(B�$B!!�(B
�$BLdBj�(B 3.12
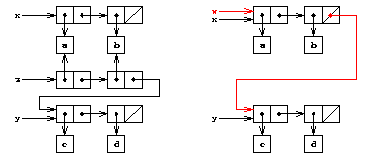
�$BLdBj�(B 3.13
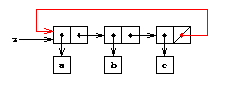
�$BLdBj�(B 3.14
(define (mystery x)
(define (loop x y)
(if (null? x)
y
(let ((temp (cdr x)))
(set-cdr! x y)
(loop temp x))))
(loop x '()))
(define v (list 'a 'b 'c 'd))
(define w (mystery v))
----- ----- ----- -----
v ->|a| +->|b| +->|c| +->|d|/|
----- ----- ----- -----
A A
| |
x y / temp
----- ----- ----- -----
v ->|a|/| |b| +->|c| +->|d|/|
----- ----- ----- -----
A A A
| | |
y x temp
v--------|
----- ---+- ----- -----
v ->|a|/| |b| | |c| +->|d|/|
----- ----- ----- -----
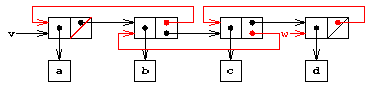
�$BLdBj�(B 3.15
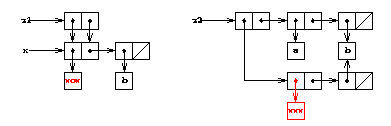
�$BLdBj�(B 3.16
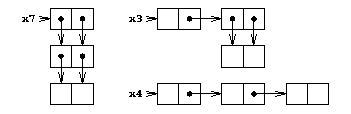
�$BLdBj�(B 3.17
(define (new-count-pairs x)
(define tracelist '())
(define (count-pairs x)
(cond ((not (pair? x)) 0)
((memq x tracelist) 0)
(else (set! tracelist (cons x tracelist))
(+ (count-pairs (car x))
(count-pairs (cdr x))
1))))
(count-pairs x))
(define a (cons 'foo 'bar))
(define b (cons a a))
(define l7 (cons b b))
(define l4 (cons a (cons 'foo a)))
(define l3 (cons (cons 'foo 'bar) (cons 'foo 'bar)))
(define c (list 'foo))
(define ll (cons 'foo (cons 'foo c)))
(set-car! c ll)
(newline)(display (new-count-pairs l7))
(newline)(display (new-count-pairs l4))
(newline)(display (new-count-pairs l3))
(newline)(display (new-count-pairs ll))
�$BLdBj�(B 3.18
;�$B6u$J�(Btracelist�$B$rMQ0U$9$k�(B.
;�$B%F%9%H$9$Y$-�(Blist�$B$rEO$jJb$-$J$,$i�(B, �$B$9$G$K�(Btracelist�$B$KEPO?$7$F$"$k$+D4$Y$k�(B.
;�$B$"$l$P�(Bcycle�$B$,$"$C$?$3$H$K$J$k�(B. �$B$J$1$l$P�(Btracelist�$B$KEPO?$7�(B, car, cdr�$B$rD4$Y$k�(B.
(define (find-cycle list)
(let ((tracelist '()))
(define (trace list)
(if (member list tracelist) #t
(begin
(set! tracelist (cons list tracelist))
(if (pair? list)
(begin(trace (car list))
(trace (cdr list)))
'()))))
(trace list)))
;test
(define (last-pair x)
(if (null? (cdr x)) x
(last-pair (cdr x))))
(define (make-cycle x)
(set-cdr! (last-pair x) x)
x)
(define x (list 'a 'b 'c))
(find-cycle x) ;->()
(define z (make-cycle x))
(find-cycle z) ;->#t
(define foo (list 'a 'b))
(find-cycle foo) ;->()
(define bar (cons foo foo))
(find-cycle bar) ;->#t
�$BLdBj�(B 3.19
;�$B$3$l$K$OM-L>$J%"%k%4%j%:%`$,CN$i$l$F$$$k�(B. 1�$BJb$:$D?J$`%]%$%s%?$H�(B2�$BJb$:$D�(B
;�$B?J$`%]%$%s%?$rMQ0U$7�(B, �$B%j%9%H$N=*C<$KCe$/A0$KN>%]%$%s%?$N;X$9@h$,F1$8$J$i�(B
;�$B%k!<%W$,B8:_$9$k�(B.
(define (loop-check x)
(define (check x0 x1)
(cond ((eq? x0 x1) #t)
((null? (cdr x1)) '())
((null? (cddr x1)) '())
(else (check (cdr x0) (cddr x1)))))
(if (and (pair? x) (pair? (cdr x)))
(check (cdr x) (cddr x))
'()))
(define foo '(0 1 2 3))
(set-cdr! (cdddr foo) foo)
(define bar '(0 1 2 3 4 5 6 7))
�$BLdBj�(B 3.21
(define (front-ptr queue) (car queue))
(define (rear-ptr queue) (cdr queue))
(define (set-front-ptr! queue item) (set-car! queue item))
(define (set-rear-ptr! queue item) (set-cdr! queue item))
(define (empty-queue? queue) (null? (front-ptr queue)))
(define (make-queue) (cons '() '()))
(define (front-queue queue)
(if (empty-queue? queue)
(error "FRONT called with an empty queue" queue)
(car (front-ptr queue))))
(define (insert-queue! queue item)
(let ((new-pair (cons item '())))
(cond ((empty-queue? queue)
(set-front-ptr! queue new-pair)
(set-rear-ptr! queue new-pair)
queue)
(else
(set-cdr! (rear-ptr queue) new-pair)
(set-rear-ptr! queue new-pair)
queue))))
(define (delete-queue! queue)
(cond ((empty-queue? queue)
(error "DELETE! called with an empty queue" queue))
(else
(set-front-ptr! queue (cdr (front-ptr queue)))
queue)))
(define (print-queue queue)
(newline) (display (front-ptr queue)))
�$BLdBj�(B 3.22
(define (make-queue)
(let ((front-ptr '())
(rear-ptr '()))
(define (front) (car front-ptr))
(define (delete!) (if (empty?) (error "DELETE! called with an empty queue" queue)
(set! front-ptr (cdr front-ptr))))
(define (empty?) (null? front-ptr))
(define (insert! item) (let ((new-item (list item)))
(cond ((empty?) (set! front-ptr new-item)
(set! rear-ptr new-item))
(else (set-cdr! rear-ptr new-item)
(set! rear-ptr (cdr rear-ptr))))))
(define (dispatch m)
(cond ((eq? m 'front) front)
((eq? m 'delete!) delete!)
((eq? m 'empty?) empty?)
((eq? m 'insert!) insert!)
(else (error "Undefined operation" m))))
dispatch))
�$BLdBj�(B 3.23
; unit-cell = (cons (cons item (cons unit-cell last)) next)
(define (front-ptr queue) (car queue))
(define (rear-ptr queue) (cdr queue))
(define (set-front-ptr! queue item) (set-car! queue item))
(define (set-rear-ptr! queue item) (set-cdr! queue item))
(define (empty-queue? queue) (null? (front-ptr queue)))
(define (make-queue) (cons '() '()))
(define (front-queue queue)
(if (empty-queue? queue)
(error "FRONT called with an empty queue" queue)
(caar (front-ptr queue))))
(define (rear-queue queue)
(if (empty-queue? queue)
(error "REAR called with an empty queue" queue)
(caaar (rear-ptr queue))))
(define (print-queue queue)
(map (lambda (x) (car x)) (front-ptr queue)))
(define (front-insert-queue! queue item)
(let ((new-item (cons (cons item (cons '() '())) '())))
(set-car! (cdar new-item) new-item)
(cond ((empty-queue? queue)
(set-front-ptr! queue new-item)
(set-rear-ptr! queue (cdar new-item))
(print-queue queue))
(else
(set-cdr! new-item (front-ptr queue))
(set-cdr! (cdar (front-ptr queue)) (cdar new-item))
(set-front-ptr! queue new-item)
(print-queue queue)))))
(define (rear-insert-queue! queue item)
(let ((new-item (cons (cons item (cons '() '())) '())))
(set-car! (cdar new-item) new-item)
(cond ((empty-queue? queue)
(set-front-ptr! queue new-item)
(set-rear-ptr! queue (cdar new-item))
(print-queue queue))
(else
(set-cdr! (cdar new-item) (rear-ptr queue))
(set-cdr! (car (rear-ptr queue)) new-item)
(set-rear-ptr! queue (cdar new-item))
(print-queue queue)))))
(define (front-delete-queue! queue)
(cond ((empty-queue? queue)
(error "DELETE! called with an empty queue" queue))
(else
(set-front-ptr! queue (cdr (front-ptr queue)))
(if (null? (front-ptr queue)) (set-rear-ptr! queue '())
(set-cdr! (cdar (front-ptr queue)) '()))
(print-queue queue))))
(define (rear-delete-queue! queue)
(cond ((empty-queue? queue)
(error "DELETE! called with an empty queue" queue))
(else
(set-rear-ptr! queue (cdr (rear-ptr queue)))
(if (null? (rear-ptr queue)) (set-front-ptr! queue '())
(set-cdr! (car (rear-ptr queue)) '()))
(print-queue queue))))
(define q (make-queue))
(front-insert-queue! q 'b)
(front-insert-queue! q 'a)
(rear-insert-queue! q 'c)
�$BLdBj�(B 3.24
(define (make-table same-key?)
(define (assoc key records)
(cond ((null? records) false)
((same-key? key (caar records)) (car records))
(else (assoc key (cdr records)))))
(let ((local-table (list '*table*)))
(define (lookup key-1 key-2)
(let ((subtable (assoc key-1 (cdr local-table))))
(if subtable
(let ((record (assoc key-2 (cdr subtable))))
(if record
(cdr record)
false))
false)))
(define (insert! key-1 key-2 value)
(let ((subtable (assoc key-1 (cdr local-table))))
(if subtable
(let ((record (assoc key-2 (cdr subtable))))
(if record
(set-cdr! record value)
(set-cdr! subtable
(cons (cons key-2 value)
(cdr subtable)))))
(set-cdr! local-table
(cons (list key-1
(cons key-2 value))
(cdr local-table)))))
'ok)
(define (dispatch m)
(cond ((eq? m 'lookup-proc) lookup)
((eq? m 'insert-proc!) insert!)
(else (error "Unknown operation -- TABLE" m))))
dispatch))
�$BLdBj�(B 3.25
(define (make-table) (list '*table*))
(define (lookup keylist table)
(let ((subtable (assoc (car keylist) (cdr table))))
(if subtable
(if (null? (cdr keylist))
(cdr subtable)
(lookup (cdr keylist) subtable))
false)))
(define (insert! keylist value table)
(let ((subtable (assoc (car keylist) (cdr table))))
(if subtable
(if (null? (cdr keylist))
(set-cdr! subtable value)
(insert! (cdr keylist) value subtable))
(set-cdr! table
(cons (if (null? (cdr keylist)) (cons (car keylist) value)
(let ((newtable (list (car keylist))))
(insert! (cdr keylist) value newtable)
newtable)) (cdr table))))))
(define table (make-table))
(insert! '(k0 k00) 0 table)
(insert! '(k1 k10) 10 table)
(insert! '(k0 k01) 1 table)
(insert! '(k2 k20) 20 table)
(insert! '(k1 k11) 11 table)
(insert! '(k0 k02) 2 table)
(insert! '(k2 k21) 21 table)
(insert! '(k1 k12) 12 table)
(insert! '(k2 k22) 22 table)
table �$B"*�(B (*table* (k2 (k22 . 22) (k21 . 21) (k20 . 20))
(k1 (k12 . 12) (k11 . 11) (k10 . 10))
(k0 (k02 . 2) (k01 . 1) (k00 . 0)))
(lookup '(k0 k00) table) �$B"*�(B 0
(lookup '(k2 k22) table) �$B"*�(B 22
�$BLdBj�(B 3.26
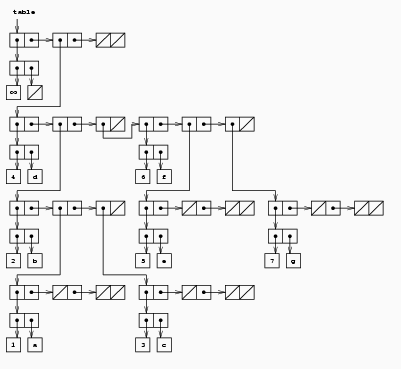
(define (make-table)
(list (cons 1000000 '()) '() '())) �$B"+�(B �$BL58BBg$N$D$b$j�(B
(define (lookup key table)
(cond ((= key (caar table)) (cdar table))
((< key (caar table))
(if (null? (cadr table)) false
(lookup key (cadr table))))
((> key (caar table))
(if (null? (caddr table)) false
(lookup key (caddr table))))))
(define (insert! key value table)
(cond ((= key (caar table)) (set-cdr! (car table) value))
((< key (caar table))
(if (null? (cadr table))
(set-car! (cdr table) (list (cons key value) '() '()))
(insert! key value (cadr table))))
((> key (caar table))
(if (null? (caddr table))
(set-car! (cddr table) (list (cons key value) '() '()))
(insert! key value (caddr table)))))
'ok)
(define table (make-table))
(insert! 4 'd table)
(insert! 2 'b table)
(insert! 1 'a table)
(insert! 3 'c table)
(insert! 6 'f table)
(insert! 5 'e table)
(insert! 7 'g table)
(insert! 4 'h table)
�$BLdBj�(B 3.27
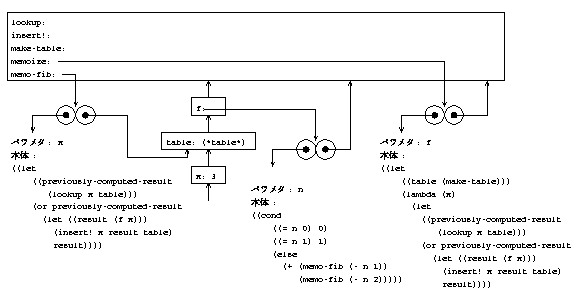
�$BLdBj�(B 3.28
(define (or-gate a1 a2 output)
(define (or-action-procedure)
(let ((new-value
(logical-or (get-signal a1) (get-signal a2))))
(after-delay or-gate-delay
(lambda ()
(set-signal! output new-value)))))
(add-action! a1 or-action-procedure)
(add-action! a2 or-action-procedure)
'ok)
(define (logical-or a b)
(cond ((and (= a 0) (= b 0)) 0)
((or (= a 1) (= b 1)) 1)
(else "Invalid signal OR" (list a b))))
�$BLdBj�(B 3.29
(define (or-gate a1 a2 output)
(let ((b1 (make-wire)) (b2 (make-wire)) (c (make-wire)))
(inverter a1 b1)
(inverter a2 b2)
(and-gate b1 b2 c)
(inverter c output)
'ok))
�$B;~4V$O�(B and-gate-delay + (2 * inverter-delay)
�$BLdBj�(B 3.30
n=4�$B$H$9$k�(B.
(define (ripple-carry-adder a1 a2 a3 a4 b1 b2 b3 b4 c4 c s1 s2 s3 s4)
(let ((c1 (make-wire)) (c2 (make-wire)) (c3 (make-wire)))
(full-adder a4 b4 c4 s4 c3)
(full-adder a3 b3 c3 s3 c2)
(full-adder a2 b2 c2 s2 c1)
(full-adder a1 b1 c1 s1 c)
'ok))
�$B;~4V$N9M;!�(B
full adder1�$BCJ$N;~4V$N:GBgCM$O�(B
sum�$B$O�(Bhalf adder�$B$N�(Bsum�$B$N;~4V$N�(B2�$BG\�(B
carry�$B$O�(Bhalf adder�$B$N�(Bsum�$B$N;~4V�(B + half adder�$B$N�(Bcarry�$B$N;~4V�(B + or�$B$N;~4V�(B
n�$BCJ$N$H$-$O�(B(carry�$B;~4V�(B �$B!_�(B (n - 1))+ (max (carry�$B;~4V�(B, sum�$B;~4V�(B)
�$B$3$N%7%_%e%l!<%?$NNc$G$O�(Bcarry�$B$N;~4V$b�(Bsum�$B$N;~4V$b�(B8�$B$J$N$G�(B, 64�$B%/%m%C%/I,MW�(B.
�$B?.9f$NEA$o$C$F$$$/MM;R$r2<$N?^$K<($9�(B.
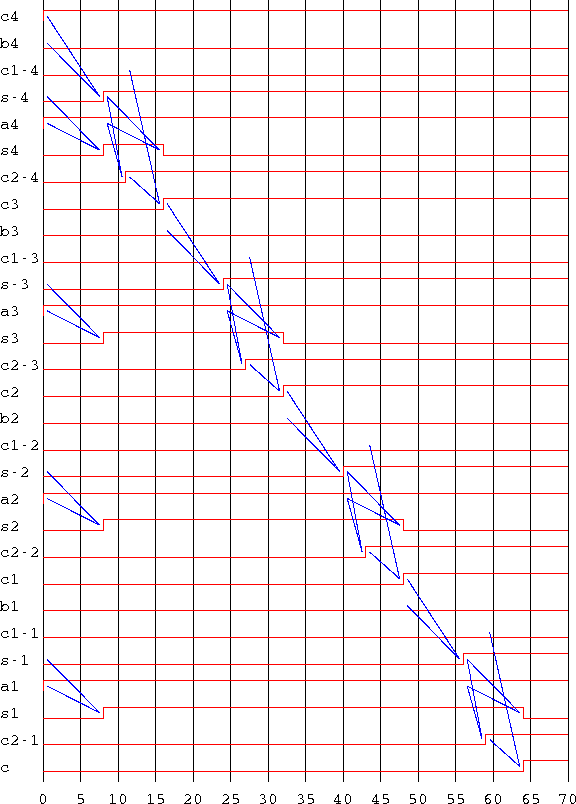
�$BLdBj�(B 3.33
(define (averager a b c)
(let ((d (make-connector)) (e (make-connector)))
(adder a b d)
(multiplier c e d)
(constant 2 e)
'ok))
(define a (make-connector))
(define b (make-connector))
(define c (make-connector))
(averager a b c)
(probe "average" c)
(probe "data-1" a)
(probe "data-2" b)
(set-value! a 18 'user)
(set-value! b 12 'user)
(forget-value! b 'user)
(set-value! c 25 'user)
�$BLdBj�(B 3.34
multiplier�$B$NDj5A$r$_$k$H�(B, product�$B$OCM$r;}$A�(B, �$B>h?t�(B, �$BHo>h?t�(B
�$B$,$H$b$KCM$r;}$?$J$$>l9g$O2?$b$7$J$$$h$&$K�(B, �$B$J$C$F$$$k�(B.
(define (squarer a b)
(multiplier a a b)
'ok)
�$B$NDj5A$G�(B
(define a (make-connector))
(define b (make-connector))
(squarer a b)
(probe "radicand" a)
(probe "square" b)
(set-value! b 64 'user)
�$B$N$h$&$K$d$C$F$_$F$b�(B, a�$B$NCM$O@_Dj$5$l$J$$�(B.
multiplier�$B$NCf$K�(B
((and (has-value? product) (>= (get-value product) 0)
(not (has-value? m1)) (not (has-value? m2)))
(set-value! m1 (sqrt (get-value product)) me)
(set-value! m2 (sqrt (get-value product)) me))
�$B$N>l9g$rDI2C$9$k$H�(B
Probe: square = 64
Probe: radicand = 8
;Value: done
�$B$N$h$&$KJ?J}:,$N7W;;$,=PMh$k�(B.
�$BLdBj�(B 3.35
(define (squarer a b)
(define (square x) (* x x))
(define (process-new-value)
(if (has-value? b)
(if (< (get-value b) 0)
(error "square less than 0 -- SQUARER" (get-value b))
(set-value! a (sqrt (get-value b)) me))
(cond ((has-value? a) (set-value! b (square (get-value a)) me)))))
(define (process-forget-value)
(forget-value! a me)
(forget-value! b me)
(process-new-value))
(define (me request)
(cond ((eq? request 'I-have-a-value)
(process-new-value))
((eq? request 'I-lost-my-value)
(process-forget-value))
(else
(error "Unknown request -- SQUARER" request))))
(connect a me)
(connect b me)
me)
;(define a (make-connector))
;(define b (make-connector))
;(squarer a b)
;(probe "radicand" a)
;(probe "square" b)
;(set-value! b 64 'user)
;(forget-value! b 'user)
;(set-value! a 12 'user)
�$BLdBj�(B 3.36
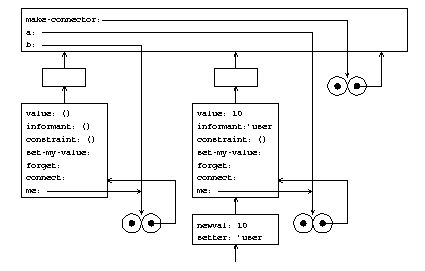
�$BLdBj�(B 3.37
(define (c+ x y)
(let ((z (make-connector)))
(adder x y z)
z))
(define (c- x y)
(let ((z (make-connector)))
(adder y z x)
z))
(define (c* x y)
(let ((z (make-connector)))
(multiplier x y z)
z))
(define (c/ x y)
(let ((z (make-connector)))
(multiplier y z x)
z))
(define (cv x)
(let ((z (make-connector)))
(constant x z)
z))
(define (celsius-fahrenheit-converter x)
(c+ (c* (c/ (cv 9) (cv 5))
x)
(cv 32)))
(define C (make-connector))
(define F (celsius-fahrenheit-converter C))
;(probe "Celsius temp" C)
;(probe "Fahrenheit temp" F)
;(set-value! C 25 'user)
�$B2sO)%7%_%e%l!<%?�(B
(define (front-ptr queue) (car queue))
(define (rear-ptr queue) (cdr queue))
(define (set-front-ptr! queue item) (set-car! queue item))
(define (set-rear-ptr! queue item) (set-cdr! queue item))
(define (empty-queue? queue) (null? (front-ptr queue)))
(define (make-queue) (cons '() '()))
(define (front-queue queue)
(if (empty-queue? queue)
(error "FRONT called with an empty queue" queue)
(car (front-ptr queue))))
(define (insert-queue! queue item)
(let ((new-pair (cons item '())))
(cond ((empty-queue? queue)
(set-front-ptr! queue new-pair)
(set-rear-ptr! queue new-pair)
queue)
(else
(set-cdr! (rear-ptr queue) new-pair)
(set-rear-ptr! queue new-pair)
queue))))
(define (delete-queue! queue)
(cond ((empty-queue? queue)
(error "DELETE! called with an empty queue" queue))
(else
(set-front-ptr! queue (cdr (front-ptr queue)))
queue)))
(define (make-time-segment time queue)
(cons time queue))
(define (segment-time s) (car s))
(define (segment-queue s) (cdr s))
(define (make-agenda) (list 0))
(define (current-time agenda) (car agenda))
(define (set-current-time! agenda time)
(set-car! agenda time))
(define (segments agenda) (cdr agenda))
(define (set-segments! agenda segments)
(set-cdr! agenda segments))
(define (first-segment agenda) (car (segments agenda)))
(define (rest-segments agenda) (cdr (segments agenda)))
(define (empty-agenda? agenda)
(null? (segments agenda)))
(define (add-to-agenda! time action agenda)
(define (belongs-before? segments)
(or (null? segments)
(< time (segment-time (car segments)))))
(define (make-new-time-segment time action)
(let ((q (make-queue)))
(insert-queue! q action)
(make-time-segment time q)))
(define (add-to-segments! segments)
(if (= (segment-time (car segments)) time)
(insert-queue! (segment-queue (car segments))
action)
(let ((rest (cdr segments)))
(if (belongs-before? rest)
(set-cdr!
segments
(cons (make-new-time-segment time action)
(cdr segments)))
(add-to-segments! rest)))))
(let ((segments (segments agenda)))
(if (belongs-before? segments)
(set-segments!
agenda
(cons (make-new-time-segment time action)
segments))
(add-to-segments! segments))))
(define (remove-first-agenda-item! agenda)
(let ((q (segment-queue (first-segment agenda))))
(delete-queue! q)
(if (empty-queue? q)
(set-segments! agenda (rest-segments agenda)))))
(define (first-agenda-item agenda)
(if (empty-agenda? agenda)
(error "Agenda is empty -- FIRST-AGENDA-ITEM")
(let ((first-seg (first-segment agenda)))
(set-current-time! agenda (segment-time first-seg))
(front-queue (segment-queue first-seg)))))
(define (half-adder a b s c)
(let ((d (make-wire)) (e (make-wire)))
(or-gate a b d)
(and-gate a b c)
(inverter c e)
(and-gate d e s)
'ok))
(define (full-adder a b c-in sum c-out)
(let ((s (make-wire))
(c1 (make-wire))
(c2 (make-wire)))
(half-adder b c-in s c1)
(half-adder a s sum c2)
(or-gate c1 c2 c-out)
'ok))
(define (inverter input output)
(define (invert-input)
(let ((new-value (logical-not (get-signal input))))
(after-delay inverter-delay
(lambda ()
(set-signal! output new-value)))))
(add-action! input invert-input)
'ok)
(define (logical-not s)
(cond ((= s 0) 1)
((= s 1) 0)
(else (error "Invalid signal" s))))
(define (and-gate a1 a2 output)
(define (and-action-procedure)
(let ((new-value
(logical-and (get-signal a1) (get-signal a2))))
(after-delay and-gate-delay
(lambda ()
(set-signal! output new-value)))))
(add-action! a1 and-action-procedure)
(add-action! a2 and-action-procedure)
'ok)
(define (logical-and a b)
(cond ((or (= a 0) (= b 0)) 0)
((and (= a 1) (= b 1)) 1)
(else "Invalid signal AND" (list a b))))
(define (or-gate a1 a2 output)
(define (or-action-procedure)
(let ((new-value
(logical-or (get-signal a1) (get-signal a2))))
(after-delay or-gate-delay
(lambda ()
(set-signal! output new-value)))))
(add-action! a1 or-action-procedure)
(add-action! a2 or-action-procedure)
'ok)
(define (logical-or a b)
(cond ((and (= a 0) (= b 0)) 0)
((or (= a 1) (= b 1)) 1)
(else "Invalid signal OR" (list a b))))
(define (make-wire)
(let ((signal-value 0) (action-procedures '()))
(define (set-my-signal! new-value)
(if (not (= signal-value new-value))
(begin (set! signal-value new-value)
(call-each action-procedures))
'done))
(define (accept-action-procedure! proc)
(set! action-procedures (cons proc action-procedures))
(proc))
(define (dispatch m)
(cond ((eq? m 'get-signal) signal-value)
((eq? m 'set-signal!) set-my-signal!)
((eq? m 'add-action!) accept-action-procedure!)
(else (error "Unknown operation -- WIRE" m))))
dispatch))
(define (call-each procedures)
(if (null? procedures)
'done
(begin
((car procedures))
(call-each (cdr procedures)))))
(define (get-signal wire)
(wire 'get-signal))
(define (set-signal! wire new-value)
((wire 'set-signal!) new-value))
(define (add-action! wire action-procedure)
((wire 'add-action!) action-procedure))
(define (after-delay delay action)
(add-to-agenda! (+ delay (current-time the-agenda))
action
the-agenda))
(define (propagate)
(if (empty-agenda? the-agenda)
'done
(let ((first-item (first-agenda-item the-agenda)))
(first-item)
(remove-first-agenda-item! the-agenda)
(propagate))))
(define (probe name wire)
(add-action! wire
(lambda ()
(newline)
(display name)
(display " ")
(display (current-time the-agenda))
(display " New-value = ")
(display (get-signal wire)))))
(define the-agenda (make-agenda))
(define inverter-delay 2)
(define and-gate-delay 3)
(define or-gate-delay 5)
(define input-1 (make-wire))
(define input-2 (make-wire))
(define sum (make-wire))
(define carry (make-wire))
(define input (make-wire))
(define output (make-wire))
;(probe 'sum sum)
;(probe 'carry carry)
;(half-adder input-1 input-2 sum carry)
;(set-signal! input-1 1)
;(propagate)
;(set-signal! input-2 1)
;(propagate)
�$B@)Ls%7%9%F%`�(B
(define (adder a1 a2 sum)
(define (process-new-value)
(cond ((and (has-value? a1) (has-value? a2))
(set-value! sum
(+ (get-value a1) (get-value a2))
me))
((and (has-value? a1) (has-value? sum))
(set-value! a2
(- (get-value sum) (get-value a1))
me))
((and (has-value? a2) (has-value? sum))
(set-value! a1
(- (get-value sum) (get-value a2))
me))))
(define (process-forget-value)
(forget-value! sum me)
(forget-value! a1 me)
(forget-value! a2 me)
(process-new-value))
(define (me request)
(cond ((eq? request 'I-have-a-value)
(process-new-value))
((eq? request 'I-lost-my-value)
(process-forget-value))
(else
(error "Unknown request -- ADDER" request))))
(connect a1 me)
(connect a2 me)
(connect sum me)
me)
(define (inform-about-value constraint)
(constraint 'I-have-a-value))
(define (inform-about-no-value constraint)
(constraint 'I-lost-my-value))
(define (multiplier m1 m2 product)
(define (process-new-value)
(cond ((or (and (has-value? m1) (= (get-value m1) 0))
(and (has-value? m2) (= (get-value m2) 0)))
(set-value! product 0 me))
((and (has-value? m1) (has-value? m2))
(set-value! product
(* (get-value m1) (get-value m2))
me))
((and (has-value? product) (has-value? m1))
(set-value! m2
(/ (get-value product) (get-value m1))
me))
((and (has-value? product) (has-value? m2))
(set-value! m1
(/ (get-value product) (get-value m2))
me))))
(define (process-forget-value)
(forget-value! product me)
(forget-value! m1 me)
(forget-value! m2 me)
(process-new-value))
(define (me request)
(cond ((eq? request 'I-have-a-value)
(process-new-value))
((eq? request 'I-lost-my-value)
(process-forget-value))
(else
(error "Unknown request -- MULTIPLIER" request))))
(connect m1 me)
(connect m2 me)
(connect product me)
me)
(define (constant value connector)
(define (me request)
(error "Unknown request -- CONSTANT" request))
(connect connector me)
(set-value! connector value me)
me)
(define (probe name connector)
(define (print-probe value)
(newline)
(display "Probe: ")
(display name)
(display " = ")
(display value))
(define (process-new-value)
(print-probe (get-value connector)))
(define (process-forget-value)
(print-probe "?"))
(define (me request)
(cond ((eq? request 'I-have-a-value)
(process-new-value))
((eq? request 'I-lost-my-value)
(process-forget-value))
(else
(error "Unknown request -- PROBE" request))))
(connect connector me)
me)
(define (make-connector)
(let ((value false) (informant false) (constraints '()))
(define (set-my-value newval setter)
(cond ((not (has-value? me))
(set! value newval)
(set! informant setter)
(for-each-except setter
inform-about-value
constraints))
((not (= value newval))
(error "Contradiction" (list value newval)))
(else 'ignored)))
(define (forget-my-value retractor)
(if (eq? retractor informant)
(begin (set! informant false)
(for-each-except retractor
inform-about-no-value
constraints))
'ignored))
(define (connect new-constraint)
(if (not (memq new-constraint constraints))
(set! constraints
(cons new-constraint constraints)))
(if (has-value? me)
(inform-about-value new-constraint))
'done)
(define (me request)
(cond ((eq? request 'has-value?)
(if informant true false))
((eq? request 'value) value)
((eq? request 'set-value!) set-my-value)
((eq? request 'forget) forget-my-value)
((eq? request 'connect) connect)
(else (error "Unknown operation -- CONNECTOR"
request))))
me))
(define (for-each-except exception procedure list)
(define (loop items)
(cond ((null? items) 'done)
((eq? (car items) exception) (loop (cdr items)))
(else (procedure (car items))
(loop (cdr items)))))
(loop list))
(define (has-value? connector)
(connector 'has-value?))
(define (get-value connector)
(connector 'value))
(define (set-value! connector new-value informant)
((connector 'set-value!) new-value informant))
(define (forget-value! connector retractor)
((connector 'forget) retractor))
(define (connect connector new-constraint)
((connector 'connect) new-constraint))
(define (celsius-fahrenheit-converter c f)
(let ((u (make-connector))
(v (make-connector))
(w (make-connector))
(x (make-connector))
(y (make-connector)))
(multiplier c w u)
(multiplier v x u)
(adder v y f)
(constant 9 w)
(constant 5 x)
(constant 32 y)
'ok))
;(define C (make-connector))
;(define F (make-connector))
;(celsius-fahrenheit-converter C F)
;(probe "Celsius temp" C)
;(probe "Fahrenheit temp" F)









