[ 目次, 前節, 次節, 索引 ]

   われわれの評価器計算機に, 駆動ループを組み込もう. これは4.1.4節のdriver-loop手続きの役を果す. 評価器は繰り返し促進記号を印字し, 式を読み込み, eval-dispatchへ行って式を評価し, 結果を印字する. 次の命令は積極制御評価器の制御列の始めの部分を形成する:29

read-eval-print-loop
  (perform (op initialize-stack))
  (perform
   (op prompt-for-input) (const ";;; EC-Eval input:"))
  (assign exp (op read))
  (assign env (op get-global-environment))
  (assign continue (label print-result))
  (goto (label eval-dispatch))

print-result
  (perform
   (op announce-output) (const ";;; EC-Eval value:"))
  (perform (op user-print) (reg val))
  (goto (label read-eval-print-loop))

   手続きの中で(apply-dispatchの示す「unknown procedure type error」のような)エラーを見つけたら, エラーメッセージを印字し駆動ループへ戻る.30

unknown-expression-type
  (assign val (const unknown-expression-type-error))
  (goto (label signal-error))


unknown-procedure-type
  (restore continue)    ; スタックを清掃する (apply-dispatchから)
  (assign val (const unknown-procedure-type-error))
  (goto (label signal-error))


signal-error
  (perform (op user-print) (reg val))
  (goto (label read-eval-print-loop))

(未定義変数のような)エラーが評価を中断した後, スタックは空ではないかも知れず, シミュレーションのためには駆動ループで毎回スタックを初期化する.31

   5.4.1--5.4.4節で述べたプログラムの断片をすべて組み合せると, 5.2節のレジスタ計算機シミュレータを使って走らせることの出来る評価器計算機モデルが作れる.

(define eceval
  (make-machine
   '(exp env val proc argl continue unev)
   eceval-operations
  '(
    read-eval-print-loop
      ⟨前述した計算機の全評価器⟩
   )))

(define eceval-operations
  (list (list 'self-evaluating? self-evaluating?)
        ⟨積極制御評価器 [eceval] 計算機の演算の全リスト⟩))

   最後に大域環境を初期化し, 評価器を走らせる.

(define the-global-environment (setup-environment))

(start eceval)

;;; EC-Eval input:
(define (append x y)
  (if (null? x)
      y
      (cons (car x)
            (append (cdr x) y))))
;;; EC-Eval value:
ok

;;; EC-Eval input:
(append '(a b c) '(d e f))
;;; EC-Eval value:
(a b c d e f)

   もちろん式のこのような評価は, 多層レベルのシミュレーションをやっているので, Schemeに直接入力したのと比べると, 非常に時間がかかる. われわれの式は積極制御評価器計算機で評価され, それはSchemeプログラムで評価され, それ自身はまたScheme解釈系で評価される.

評価器の性能監視

print-result
  (perform (op print-stack-statistics)); 命令を追加
  (perform
   (op announce-output) (const ";;; EC-Eval value:"))
   ... ; 前と同様

;;; EC-Eval input:
(define (factorial n)
  (if (= n 1)
      1
      (* (factorial (- n 1)) n)))
(total-pushes = 3 maximum-depth = 3)
;;; EC-Eval value:
ok

;;; EC-Eval input:
(factorial 5)
(total-pushes = 144 maximum-depth = 28)
;;; EC-Eval value:
120

(define (factorial n)
  (define (iter product counter)
    (if (> counter n)
        product
        (iter (* counter product)
              (+ counter 1))))
  (iter 1 1))

(define (factorial n)
  (if (= n 1)
      1
      (* (factorial (- n 1)) n)))

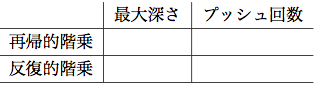
(define (fib n)
  (if (< n 2)
      n
      (+ (fib (- n 1)) (fib (- n 2)))))

29 ここではread や各種の印字演算は基本的な機械演算として使用可能と仮定する. この仮定はシミュレーションには有用だが, 実際的には現実的ではない. これらは非常に複雑な演算である. 実際には, 一文字を外部装置とやりとりする低レベル入出力演算を使って実装する.

get-global-environment演算を実現するため

(define the-global-environment (setup-environment))

(define (get-global-environment)
  the-global-environment)

[ 目次, 前節, 次節, 索引 ]