計算機メモリーをモデル化するため,
ベクタ(vector)という新しい種類のデータ構造を使う. 抽象的にはベクタは合成データオブジェクトである. 各要素は整数の添字を使い, 添字とは独立の時間でアクセス出来る.
5
メモリー演算を記述するには, ベクタを操作するSchemeの基本的手続きを二つ使う:
•
(vector-ref ⟨vector⟩ ⟨n⟩)はベクタのn番目の要素を返す.
•
(vector-set! ⟨vector⟩ ⟨n⟩ ⟨value⟩)
はベクタのn番目の要素を, 指定した値に設定する.
例えば, vをベクタとして, (vector-ref v 5)はベクタvの5番目の項を取り出し, (vector-set! v 5 7)はベクタvの5番目の項の値を7に変更する.6
計算機メモリーでは,
このアクセスは, メモリーでのベクタの先頭番地を規定するベースアドレス(base address)とベクタ中の特定の要素の距離を規定する添字
(index)を組み合せるアドレス演算を使って実装出来る.
n4のような整数へのポインタは, 数値データを示す型と, 整数4の実際の表現とからなるであろう.9 ポインタ一個に割り当てられた固定の大きさのスペースで表記するには大き過ぎる整数を扱うには, 別の ビッグナム(bignum)データ型を使う. この型では, ポインタは整数の各部分を格納するリストを指定している.10
記号は, 記号の印字表現を形成する文字の並びを指示する型つきポインタで表す. この並びは文字列が入力に最初に現れた時に, Lispの読込みルーチンが構成する. 一つの記号の二つの実体が eq?で「同じ」記号として認めて貰いたいし, eq?をポインタの等価の単純なテストとしたいので, 読込みルーチンが同じ文字列を二度見た時, その二度の出現に(同じ文字の並びへの)同じポインタを使うよう保証しなければならない. これを実現するため, 読込みルーチンは, 伝統的に オブアレイ(obarray)という, それまでに出会ったすべての記号の表を保持する. 読込みルーチンが文字列を見つけ, 記号を構成しようとする時, 同じ文字列を以前に見たことがあるか知るため, オブアレイを調べる. まだ見たことがなければ, 文字列を使って新しい記号(新しい文字列への型つきポインタ)を構成し, このポインタをオブアレイに入れる. 読込みルーチンがこの文字列を以前に見たことがあれば, オブアレイに格納されている記号のポインタを返す. この文字列を一意的ポインタに取り替える処理を, 記号の インターン(interning)[閉じ込めるの意]という.
(assign ⟨reg1⟩ (op car) (reg ⟨reg2⟩)) (assign ⟨reg1⟩ (op cdr) (reg ⟨reg2⟩))は, これらのそれぞれを
(assign ⟨reg1⟩ (op vector-ref) (reg the-cars) (reg ⟨reg2⟩)) (assign ⟨reg1⟩ (op vector-ref) (reg the-cdrs) (reg ⟨reg2⟩))と実装すればレジスタ計算機で実現出来る. 命令
(perform (op set-car!) (reg ⟨reg1⟩) (reg ⟨reg2⟩)) (perform (op set-cdr!) (reg ⟨reg1⟩) (reg ⟨reg2⟩))は
(perform (op vector-set!) (reg the-cars) (reg ⟨reg1⟩) (reg ⟨reg2⟩)) (perform (op vector-set!) (reg the-cdrs) (reg ⟨reg1⟩) (reg ⟨reg2⟩))と実装する.
consは未使用の添字を割り当て, consの引数をthe-carsとthe-cdrsのその添字の指すベクタの位置に格納して実行する. 特別なレジスタ freeがあって, 次に使用可能な添字を持つ対へのポインタを保持しており, 次の空き場所を見つけるために, そのポインタの添字部分を増やすことが出来ると仮定する.11 例えば命令
(assign ⟨reg1⟩ (op cons) (reg ⟨reg2⟩) (reg ⟨reg3⟩))は, 次の一連のベクタ演算で実装する.12
(perform (op vector-set!) (reg the-cars) (reg free) (reg ⟨reg2⟩)) (perform (op vector-set!) (reg the-cdrs) (reg free) (reg ⟨reg3⟩)) (assign ⟨reg1⟩ (reg free)) (assign free (op +) (reg free) (const 1))eq?演算
(op eq?) (reg ⟨reg1⟩) (reg ⟨reg2⟩)はレジスタの全フィールドの等価をテストし, pair?, null?, symbol?およびmember?のような述語は, 型フィールドを調べるだけが必要である.
(assign the-stack (op cons) (reg ⟨reg⟩) (reg the-stack))と実現出来る. 同様に(restore ⟨reg⟩)は
(assign ⟨reg⟩ (op car) (reg the-stack)) (assign the-stack (op cdr) (reg the-stack))と実現出来, また(perform (op initialize-stack))は
(assign the-stack (const ()))と実現出来る. これらの演算は上述のベクタ演算を使って更に展開出来る. しかし通常の計算機アーキテクチャでは, スタックは別のベクタに割り当てるのが得策である. そうすればスタックのプッシュとポップは, そのベクタへの添字の増減で実現出来る.
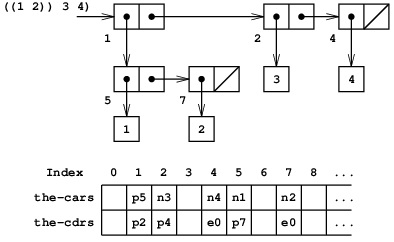
(define x (cons 1 2)) (define y (list x x))で作られたリスト構造の箱とポインタ表記およびfreeポインタは最初にp1 であるとして, (図5.14のような)メモリーベクタ表現を描け. freeの最後の値は何か. どのポインタがxとyの値を表しているか.
(define (count-leaves tree)
(cond ((null? tree) 0)
((not (pair? tree)) 1)
(else (+ (count-leaves (car tree))
(count-leaves (cdr tree))))))
b. カウンタを陽に持つ再帰的count-leaves:
(define (count-leaves tree)
(define (count-iter tree n)
(cond ((null? tree) n)
((not (pair? tree)) (+ n 1))
(else (count-iter (cdr tree)
(count-iter (car tree) n)))))
(count-iter tree 0))
5
メモリーを項目のリストで表現することも出来る. しかしリストのn番目の要素のアクセスは, n - 1回のcdr演算を必要とするので, アクセス時間は添字とは独立でない.
6
完全のためには, ベクタを構成する
make-vector演算を規定しなければならない. しかし今の応用では, ベクタは計算機メモリーの固定部分をモデル化するだけに使う.
7
これは2章で, 汎用演算を扱った時に紹介した
「タグつきデータ」の考え方と全く同じである. しかしここでは, データ型は, リストを使って構成したのではなく, 基本的な機械レベルで組み込まれている.
8
型情報は, Lispシステムを実装する計算機の細部に従い, いろいろな方法でコード化される. Lispプログラムの実行効率は, これをいかに賢明に選択したかに強く依存するが, うまい選択の一般的設計規則を形式化するのは難しい. 型つきポインタの最も直截な方法は, 各ポインタの決ったビットの位置を, データ型をコード化する
型フィールド(type field)にしてしまうことである. こういう表現を設計する時に考えるべき重要な問題には, 次のものがある: つまり型に何ビットが必要か, ベクタの添字は最大どのくらい必要か. 基本的計算機命令で, ポインタの型フィールドがどの位効率よく操作出来るか, など. 型フィールドが効率よく扱える特別なハードウェアを持つ計算機は
タグアーキテクチャ(tagged
architecture)を持つという.
9
数の表現のこの決定は, ポインタの等価をテストするeq?が整数の等価に使えるかどうかを決定する. ポインタが数自身を含むなら, 等価の数は同じポインタを持つであろう. しかしポインタが数の格納してある場所の添字を持つなら, 同じ整数を複数の場所に格納しないように注意した時だけ, 等しい数が等しいポインタを持つことを保証する.
10
これは整数を数字の並びとして書くようなものである. ただし各「数字」は0から一個のポインタとして格納出来る最大数までの間の整数である.
11
空き場所を見つける別な方法もある.
例えば未使用の対のすべてを
フリーリスト(free list)につなぐことが出来る. 5.3.2節で見るように, 詰込み式のごみ集めを利用するので, われわれの空き場所は連続的である. (従ってポインタを増やすことでアクセス出来る.)
12
これは本質的に3.3.1節に述べたようにset-car!とset-cdr!を使ってのconsの実装である. あの実装で使った演算get-new-pairはここではfreeポインタで実現している.