[ 目次, 前節, 次節, 索引 ]

   しかし再帰的プロセスの実装は, 追加の機構を必要とする. 1.2.1節で最初に調べた階乗を計算する再帰的プロセスを考えよう:

(define (factorial n)
  (if (= n 1)
      1
      (* (factorial (- n 1)) n)))

(define (gcd a b)
  (if (= b 0)
      a
      (gcd b (remainder a b))))

   階乗(や再帰プロセス)の場合は, 新しい階乗下請け問題の答は元々の問題の答ではない. 最終の答を得るには, (n - 1)!で得た結果にnを掛けなければならない. GCDの設計を模倣し, 階乗の下請け問題をnレジスタを減算し, 階乗計算機を再実行して解くなら, 結果に掛けるべきnの昔の値はもはや使用可能ではない. 従って下請け問題で仕事する第二の階乗計算機が必要になる. この第二の階乗計算自身には, 第三の階乗計算機を必要とする階乗下請け問題があり, これが続く. 各階乗計算機はその中にもう一つの階乗計算機を持つから, 計算機全体では類似の計算機の無限の入れ子になり, 固定有限の部品で構成することは出来ない.

   それにも拘らず, 同じ部品を計算機の入れ子の各実体として使うようにすれば, 階乗プロセスをレジスタ計算機として実装出来る. 特にn!を計算する計算機は(n - 1)!を計算する下請け問題, (n - 2)!を計算する下請け問題などに同一の部品を使うべきである. 階乗のプロセスは, 計算を実行するのに同じ計算機の限りなく多くのコピーを必要とするが, ある時刻にはこれらのコピーの一つだけが活動している必要があるだけなので, これは可能である. 計算機が再帰的な下請け問題に出会った時, それは主問題の仕事を中断し, 同じ物理的部分を下請け問題の仕事に再利用し, その後中断した計算を続行する.

   下請け問題では, レジスタの内容は主問題であったのとは違うであろう. (今の場合はnレジスタは減数される.) 中断した計算が続行出来るためには, これらが中断した計算を続行する時, 回復出来るように, 下請け問題が解けた後, 必要になるレジスタの内容を退避しなければならない. 階乗の場合は減数したnレジスタの階乗の計算が済んだ時, 回復出来るようにn の古い値を退避する.2

   入れ子の再帰的呼出しの深さには, 先験的な上限はないので, レジスタの値を任意個退避する必要がある. これらの値は, 再帰の入れ子では, 入ってきた最後の下請け問題が最初に終了するから, 退避したのと逆順で回復しなければならない. これはレジスタの値を退避するのに, スタック(stack) または「先入れ後出し」データ構造の使用を指示する. われわれは二つの命令: つまり値をスタックに置くのに使うsave命令と, スタックから回復するのに使うrestore命令を追加して, レジスタ計算機にスタックが使えるよう拡張する. 一連の値がスタックにsaveされた後, 一連のrestoreはこれらの値を逆順に取り出す.3

   スタックの助けで, 階乗計算のデータパスの単一のコピーを, 階乗の下請けの各問題に再利用出来る. データパスを操作する制御列の再利用についても, 似たような設計の論点がある. 階乗計算を再実行するのに, (n - 1)!の下請け問題を解いた後, 計算機はまだ結果にnを掛けなければならないので, 制御器は反復プロセスの時のように, 単に先頭にループして戻るわけにはいかない. 制御器はn!の計算を中断し, (n - 1)!下請け問題を解き, 更にn!の計算を続行しなければならない. 階乗計算のこの見方は, 5.1.3節に述べた, サブルーチン機構の利用を示唆する. 命令列の下請け問題を解く部分へ移行し, 後に主問題から飛び出したところから続行するため, 制御器に continueレジスタを使わせる. こうしてcontinueレジスタに格納された入り口へ戻る階乗サブルーチンを作ることが出来る. 階乗計算の各「レベル」が同じcontinue レジスタを使うことになるので, サブルーチンの各呼出しで, nレジスタでやるようにcontinueも退避, 回復する. つまり階乗サブルーチンは, 下請け問題のために自分自身を呼び出す時, continueに新しい値を置かなければならない. しかし下請け問題を解くべくそれを呼び出した場所に戻るため, 古い値も必要になる.

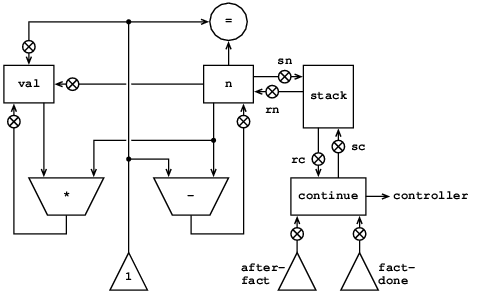
(controller
   (assign continue (label fact-done))     ; 最終帰り番地設定
 fact-loop
   (test (op =) (reg n) (const 1))
   (branch (label base-case))
   ;;nとcontinueを退避し再帰呼出しを設定する.
   ;; 再帰呼出しから戻る時after-fact}から
   ;; 計算が続行するようにcontinueを設定
   (save continue)
   (save n)
   (assign n (op -) (reg n) (const 1))
   (assign continue (label after-fact))
   (goto (label fact-loop))
 after-fact
   (restore n)
   (restore continue)
   (assign val (op *) (reg n) (reg val))   ; valに n(n-1)!がある
   (goto (reg continue))                   ; 呼出し側に戻る
 base-case
   (assign val (const 1))                  ; 基底の場合: 1!=1
   (goto (reg continue))                   ; 呼出し側に戻る
 fact-done)

   図5.11は, 再帰factorial手続きを実装する計算機のデータパスと制御器を示す. 計算機はスタックとn, valおよびcontinueという三つのレジスタを持つ. データパス図を単純化するため, レジスタ代入ボタンは名前をつけず, スタック操作ボタンにだけつけた. (scとsnはレジスタを退避する. rcおよびrnはレジスタを回復する.) 計算機を操作するには, レジスタnにその階乗が計算したい数を置き, 計算機を実行開始させる. 計算機がfact-doneに達すると, 計算は終了し, 答はvalレジスタに残る. 制御列でnと continueは, 各再帰呼出しの前で退避され, 呼出しから戻ると回復される. 呼出しからの戻りはcontinue に格納された場所へ分岐することで実現する. continueは計算機が実行開始した時, 最後の戻りでfact-doneへ行くよう初期化する. 階乗計算の結果を保持するvalレジスタは, valの古い内容はサブルーチンから戻った後は使わないので, 再帰呼出しの前に退避はしない. 下請け計算で出来た値である新しい値だけが必要である.

   階乗計算は, 原理的には無限個の計算機が必要であるが, 図5.11の計算機は, 可能性として無制限のスタックを除き, 有限である. しかしスタックの何らかの物理的実装は有限の大きさであり, これが計算機に扱える再帰呼出しの深さを制限する. 階乗のこの実装は, 再帰アルゴリズムを, スタックで増強した通常のレジスタ計算機として実現する一般的戦略を示す. 再帰的下請け問題に出会った時, その現在の値が, 下請け問題が解けた後で必要になるレジスタをスタックに退避し, 下請け再帰問題を解き, それから退避したレジスタを回復して主問題の実行を続行する. continueレジスタは常に退避しなければならない. 他に退避する必要のあるレジスタがあるかどうかは, すべての再帰計算が下請け問題の計算中に変更されるレジスタの元々の値を必要とするとは限らないので, それぞれの計算機に依存する(問題5.4参照).

二重再帰

(define (fib n)
  (if (< n 2)
      n
      (+ (fib (- n 1)) (fib (- n 2)))))

(controller
   (assign continue (label fib-done))
 fib-loop
   (test (op <) (reg n) (const 2))
   (branch (label immediate-answer))
   ;; Fib(n-1)を計算するよう設定
   (save continue)
   (assign continue (label afterfib-n-1))
   (save n)                           ; nの昔の値を退避
   (assign n (op -) (reg n) (const 1)); nを n-1 に変える
   (goto (label fib-loop))            ; 再帰呼出しを実行
 afterfib-n-1                         ; 戻った時 Fib(n-1)はvalにある
   (restore n)
   (restore continue)
   ;; Fib(n-2)を計算するよう設定
   (assign n (op -) (reg n) (const 2))
   (save continue)
   (assign continue (label afterfib-n-2))
   (save val)                         ; Fib(n-1)を退避
   (goto (label fib-loop))
 afterfib-n-2                         ; 戻った時Fib(n-2)の値はvalにある
   (assign n (reg val))               ; nにはFib(n-2)がある
   (restore val)                      ; valにはFib(n-1)がある
   (restore continue)
   (assign val                        ; Fib(n-1)+Fib(n-2)
           (op +) (reg val) (reg n))
   (goto (reg continue))              ; 呼出し側に戻る. 答えはvalにある
 immediate-answer
   (assign val (reg n))               ; 基底の場合: Fib(n)=n
   (goto (reg continue))
 fib-done)

(define (expt b n)
  (if (= n 0)
      1
      (* b (expt b (- n 1)))))

(define (expt b n)
  (define (expt-iter counter product)
    (if (= counter 0)
        product
        (expt-iter (- counter 1) (* b product))))
  (expt-iter n 1))

2 古いnを退避する必要はないという人がいるかも知れない; それを減数し, 下請け問題を解いた後, 古い値を取り戻すにには, ただ増数すればよい. この戦略は階乗には使えるが, レジスタの古い値は必ずしも新しい値からは計算出来ないので, 一般的には使えない.

3 5.3節でスタックを更に基本的な演算を使って実装する方法を見る.

[ 目次, 前節, 次節, 索引 ]