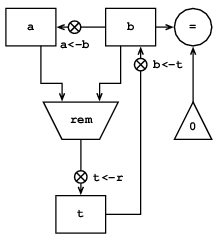
図5.1 GCD計算機のデータパス図
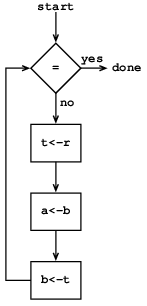
図5.2 GCD計算機の制御図
(define (gcd a b)
(if (= b 0)
a
(gcd b (remainder a b))))
このアルゴリズムを実行する計算機は二つの数aとbを覚えておかなければならない. そこでこれらの数はその名前のついたレジスタに格納されていると仮定する. 必要な基本演算はレジスタbの内容が零かどうかテストすることと, レジスタa
の内容をレジスタbの内容で割った剰余を計算することである. 剰余の演算は複雑なプロセスだが, とりあえずは剰余を計算する基本装置があると仮定する. GCDアルゴリズムの各サイクルで, レジスタaの内容はレジスタbの内容で取り替えられ, レジスタbの内容は昔のaの内容を昔のbの内容で割った剰余で取り替えられる. これらの取替えが同時に出来れば便利であろうが, われわれのレジスタ計算機のモデルでは, 各ステップで唯一つのレジスタだけに新しい値が代入されると仮定する. 取替えを実現するには, 計算機は第三の「一時的」レジスタを使う.
それをtと呼ぶ. (まず剰余をtに置き, 次にbの内容を
aに置き, 最後にtに格納された剰余をbに置く.)

図5.1 GCD計算機のデータパス図

図5.2 GCD計算機の制御図
この計算機に必要なレジスタと演算を図5.1のデータパス図を使って示すことが出来る. この図でレジスタ(a, bおよびt)は長方形で表す. 値をレジスタに代入する道は, 矢先の後にXのついた, データの源からレジスタを指す矢印で示す. Xは, これを押すと源の値が指示したレジスタへ「流れる」のを許すボタンと考えることが出来る. ボタンの隣のラベルは, ボタンを参照するのに使う名前である. 名前は任意であり, 記憶用の値を持つように選ぶ. (例えばa<-bはレジスタb の内容をレジスタaへ代入するボタンを押すことを示す.) レジスタへのデータの源は, (a<-bの代入のような)別のレジスタでも, (t<-rの代入のような)演算結果でも, (変更出来ない基本の値で, データパス図では定数を含んだ三角形で表現する) 定数でもよい.
定数とレジスタの内容から値を計算する演算は, データパス図では, 演算の名前を含む台形で表す. 例えば図5.1のremと印した箱は, それが接続されているレジスタaとbの内容の剰余を計算する演算を示す. (ボタンのない)矢印が入力のレジスタや定数から箱を指し, また矢印が演算の出力値をレジスタへ結ぶ. テストはテストの名前を含んだ円で表す. 例えばGCD計算機には, レジスタbの内容が零かどうかテストする演算がある. テストは入力のレジスタや定数からの矢印を持つが, 出力の矢印はない; その値はデータパスではなく, 制御器が使う. 全体としてデータパス図は計算機に必要なレジスタと演算, およびそれがどう接続されるかを示す. 矢印を電線, Xボタンをスイッチと見るなら, データパス図は電気部品で構成した計算機の配線図に非常によく似ている.
データパスがGCDを実際に計算するには, ボタンを正しい順で押さなければならない.
この順を図5.2に示すように制御図を使って記述する. 制御図の要素は, データパス部品をどう操作するかを示す. 制御図の四角い箱は, 押すべきデータパスのボタンを示し,
矢印はあるステップから次への順を示す. 図の菱形は, 判定を表す. 菱形で示したデータパスの値により, 二つの道順の一つに進む. 制御器は物理的類推を使って解釈出来る: 図を球の転がる迷路としよう. 球が箱に走り込むと, 箱についている名前のデータパスボタンを押す. 球が(b = 0のテストのような)判定箱に達すると, 示されたテストの結果で決る道へ抜けていく. データパスと制御器は一緒になってGCDを計算する機械を完全に記述する. まず, レジスタaとbに数を置いた後, 制御器(転がる球)をstartと印した場所に置く. 制御器がdoneに達した時, GCDの値はレジスタaにある.
問題 5.1
次の手続きが指定する反復的アルゴリズムを使い, 階乗を計算するレジスタ計算機を設計せよ. この計算機のデータパス図, 制御図を描け.
(define (factorial n)
(define (iter product counter)
(if (> counter n)
product
(iter (* counter product)
(+ counter 1))))
(iter 1 1))