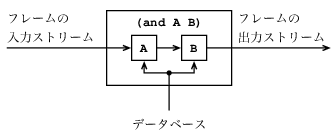
図4.5 二つの質問のand組合せはフレームのストリームに直列に操作して生成される
質問評価器は, データベースにある事実や規則に質問をマッチさせるための, ある種の探索を実行しなければならないことを, はっきりさせておこう. その一つの方法は, 質問システムを(4.3節のamb評価器を使い), 非決定性プログラムとして実装することであろう(問題4.78参照). もう一つの可能性はストリームの助けを借りて, 探索を管理することである. われわれの実装は第二の解決法に従う.
質問システムはパターンマッチング(pattern matching)とユニフィケーション(unification)という二つの中心的演算の周囲に構築する. まずパターンマッチングを述べ, この演算が, フレームのストリームを使った情報の構成とともに, 単純と合成の質問をどう実装させるかを述べる. 次にユニフィケーション, つまり規則を実装するのに必要なパターンマッチングの一般化を論じる. 最後に4.1節に述べた解釈系でevalが式を分類したのと似た方法で, 式を分類する手続きにより, 質問解釈系全体を合体させる方法を示す.
質問システムが使うパターンマッチャは, 入力としてパターン, データおよびいろいろなパターン変数の束縛を規定するフレーム(frame)をとる. それはフレームにすでにある束縛と矛盾しない方法で, データがパターンにマッチするかどうかチェックする. そうであれば, 与えられたフレームの, このマッチで決められた束縛で拡張したものを返す. そうでなければ, マッチは失敗したと表示する.
例えば, パターン(?x ?y ?x)を空のフレームで(a b a)にマッチさせようとすると, ?xはaに束縛され, ?yはbに束縛されていること規定するフレームを返す. 同じパターン, 同じデータと, ?yはaに束縛されているということを規定するフレームでマッチしようとすると, 失敗する. 同じパターン, 同じデータで, ?yはbに束縛され, ?xは未束縛であるフレームでのマッチの試みは, 与えられたフレームで, ?xのaへの束縛で拡張されたものを返す.
パターンマッチャは, 規則を持たない単純質問を処理するために必要な機構のすべてである. 例えば質問
(job ?x (computer programmer))を処理するには, データベースのすべての表明を走査し, 初期の空フレームについてパターンマッチしたものを選ぶ. マッチを見つける度に, マッチの返したフレームを使い, パターンを?xの値で具体化する.
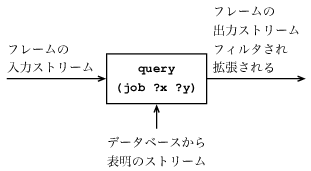
われわれのシステムでは, 質問はフレームの入力ストリームをとり, 図4.4に示すように, ストリームの各フレームに対し, 上述のマッチング演算を行う. つまり, 入力ストリームの各フレームに対し, 質問はデータベースの表明とマッチすることで出来たそのフレームに対する拡張のすべてからなる, 新しいストリームを生成する. これらのストリームのすべては, 次に組み合されて, 入力ストリームの各フレームに対するすべての可能な拡張を含む, 一つの大きなストリームが形成される. このストリームが質問の出力である.
単純質問に答えるには, 単一の空フレームからなる入力ストリームを持った質問を使う. 結果の出力ストリームは, 空フレームに対するすべての拡張(つまり質問に対するすべての回答)を含む. このフレームのストリームは, 各フレームの値で具体化された変数を持つ元々の質問パターンのコピーのストリームを生成するのに使われ,
そのストリームが最後に印字される.

図4.5 二つの質問のand組合せはフレームのストリームに直列に操作して生成される
(and (can-do-job ?x (computer programmer trainee))
(job ?person ?x))
(つまり, 「プログラム訓練生の仕事が出来る人すべてを見つけよ」)のように二つの質問の
and
を扱うには, まずパターン(can-do-job ?x (computer programmer trainee))にマッチするすべての事項を見つける. この結果, それぞれが?xへの束縛を含んだフレームのストリームが出来る. 次にこのストリームの各フレームに対し
(job ?person ?x)に, 与えられた?xの束縛と矛盾しないようにマッチする事項を見つける. このマッチのそれぞれは?xと?personの束縛を含んだフレームを生成する. 二つの質問のandは, 図4.5に示すように, 二つの要素となる質問の直列の組合せと見ることが出来る. 最初の質問のフィルタを通過したフレームは, 次の質問でフィルタされ, 更に拡張される.
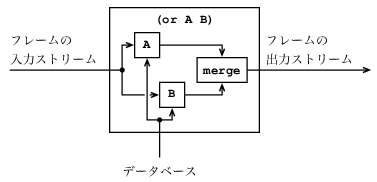
図4.6は二つの要素の質問の並列組合せとして, 二つの質問のorを計算する類似の方法を示す. フレームの入力ストリームは, それぞれの質問で別々に拡張される. 二つの結果のストリームは次に混ぜ合され, 最後の出力ストリームが作られる.
この高水準の記述からでも, 合成質問の処理は遅いということが明らかである. 例えば, 一つの質問は, 各入力フレームに一つを超えるフレームを作り出し, andの各質問は, 前の質問から入力フレームを得るので, andの各質問は最悪の場合, 質問の数の指数的な数のマッチを実行しなければならない(問題4.76参照).68 単純な質問だけを扱うシステムは, 実際的であるが, 複雑な質問の扱いは非常に難しい.69
フレームのストリームという視点からは, 質問のnotは, 質問が満足するフレームをすべて除去するフィルタとして働く. 例えばパターン
(not (job ?x (computer programmer)))が与えられたとして, 入力ストリームの各フレームから(job ?x (computer programmer))を満足する拡張フレームを作ろうとする. われわれは入力ストリームからその拡張が存在するすべてのフレームを除去する. 結果は?xの束縛が(job ?x (computer programmer))を満足しないフレームからなるストリームである. 例えば質問
(and (supervisor ?x ?y)
(not (job ?x (computer programmer))))
を処理するのに, 最初の節は?xと?yの束縛のフレームを生成する.
次にnot節は, ?xの束縛が?xが計算機プログラマであるという制限を満すフレームをこれから除去することで, フィルタする.70
lisp-value特殊形式は, フレームのストリームに対する類似のフィルタとして実装する. ストリームの各フレームを使い, パターンの変数を具体化し, 次にLispの述語を作用させる. 次にわれわれは入力ストリームから, 述語が失敗したすべてのフレームを除去する.
ユニファイアは, それぞれが定数と変数を含む二つのパターンをとり, 二つのパターンが等価になるように変数に値を代入することが可能かどうかを決定する. 可能な場合は, その束縛のフレームを返す. 例えば(?x a ?y)と(?y ?z a)のユニファイは, ?x, ?yと?zのすべてはaに束縛すべきだというフレームを返す. 他方(?x ?y a)と(?x b ?y)のユニファイは, 二つのパターンを等価にする?yの値がないため, 失敗する. (パターンの第二の要素が等価になるためには, ?yはbでなければならない; しかし第三の要素が等価になるためには, ?yはaでなければならない.) 質問システムに使われるユニファイアは, パターンマッチャに似て, 入力としてフレームをとり, フレームと矛盾しないようなユニフィケーションを実行する.
ユニフィケーションアルゴリズムは, 質問システムの技術的にもっとも難しい部分である. 複雑なパターンでは, ユニフィケーションの実行は, 推論を必要とする. 例えば(?x ?x)と((a ?y c) (a b ?z))のユニファイでは, アルゴリズムは?xは(a b c), ?yはb, そして?zはcであるべきだと推論しなければならない. この処理は, パターンの要素間の一組の式を解くと考えてよい. 一般に, 解くのに相当な処理を必要とする連立式がある.71 例えば(?x ?x)と((a ?y c) (a b ?z))のユニファイは連立方程式
?x = (a ?y c) ?x = (a b ?z)を規定すると考えられる. これらの式は
(a ?y c) = (a b ?z)を意味し, それは次に
a = a, ?y = b, c = ?z,を意味し, 従って
?x = (a b c)である.
パターンマッチが成功すると, すべてのパターン変数は束縛され, 束縛された値は定数のみからなる. このことはすでに見てきたユニフィケーションの例のすべてについて当てはまる. しかし一般的には成功したユニフィケーションは, 必ずしも変数の値を完全に決めているとは限らない; 変数のあるものは未束縛のままだし, あるものは変数を含む値に束縛されている.
(?x a)と((b ?y) ?z)のユニフィケーションを考えよう. ?x = (b ?y)およびa = ?zと推論出来る. しかし?xと?yにつき, これ以上は解けない. ?xと?yに値を代入することで, 確かに二つのパターンを等価に出来るから, ユニフィケーションは失敗ではない. このマッチは, ?yのとり得る値に制限しないので, 結果のフレームに?yの束縛はない. しかしこのマッチは?xの値を制限する. ?yの値が何であれ, ?xは(b ?y)でなければならない. 従って?x のパターン(b ?y)に対する束縛はフレームにおかれる. 後になって(このフレームと矛盾しないように要求されたパターンマッチやユニフィケーションにより,) ?yの値が決まり, フレームに追加されると, 前に束縛された?xはこの値を参照することになる.~72
(lives-near ?x (Hacker Alyssa P))のような, 規則の作用を持つ質問の処理を考えよう. この質問の処理には, このパターンにマッチする表明がデータベースにあるか見るため, まず上述の通常のパターンマッチ手続きを使う. (データベースには, 誰が誰の近くに住むかの直接的な表明はないので, 今の場合そういものはない.) 次のステップは, 質問パターンを各規則の結論とユニファイしようとすることである. パターンは規則
(rule (lives-near ?person-1 ?person-2)
(and (address ?person-1 (?town . ?rest-1))
(address ?person-2 (?town . ?rest-2))
(not (same ?person-1 ?person-2))))
の結論とユニファイすることがわかり, 結果として?person-2が(Hacker Alyssa P)に束縛され, ?xは?person-1
(と同じ値を持つよう)に束縛しなければならないと規定するフレームが出来る. 次にこのフレームとの関係で,
規則の本体の合成質問を評価する. マッチが成功し, ?person-1の束縛, 従って?xの値を用意することでフレームが拡張され, それを元々の質問パターンを具体化するのに使うことが出来る.
一般に質問評価器は, パターン変数のあるものの束縛を規定したフレームの中で, 質問パターンを確定しようとする時, 規則を作用させる次の方法を使う:
• 質問と規則の結論をユニファイし, 成功すれば元々のフレームの拡張を形成する.
• 拡張されたフレームとの関係で, 規則の本体で形成された質問を評価する.
これがLispのeval/apply評価器における手続きの作用の方法:
• 手続きのパラメタを引数と束縛し, 元々の手続き環境を拡張したフレームを形成する.
• 拡張された環境との関係で, 手続きの本体で形成された式を評価する.
と似ていることに注意しよう. 二つの評価器の間の類似は驚くに当らない. 手続き定義がLispの抽象の手段であったように, 規則の定義は質問言語の抽象の手段である. どちらの場合も, 適切な束縛を作り出し, これとの関係で規則や手続きの本体を評価することで抽象を解きほどく.
質問パターンとフレームのストリームが与えられると, 入力ストリームの各フレームについて:
• パターンをデータベースのすべての表明に(パターンマッチャを使って)マッチさせて得られた拡張フレームのストリーム
• 可能性ある規則を(ユニファイアを使って)作用させて得られた拡張フレームのストリーム73
の二つのストリームが出来る. 二つのストリームを連結すると, 与えられたパターンが, 元々のフレームと矛盾なく満足するあらゆる方法からなるストリームが出来上がる.
この(入力ストリームの各フレームに一つずつの)ストリームは組み合されて一つの大きなストリームを形成し, それは従って元々の入力ストリームにあるフレームのいずれかを, 与えられたパターンと矛盾しないマッチを生じるために拡張させるすべての方法を含んでいる.
本章の他の評価器のdriver-loop手続きと類似の駆動ループは, 端末から質問を読み込む. 各質問に対し質問と単一の空フレームからなるストリームで, qevalを呼び出す. すると(空フレームの拡張として)すべての可能なマッチのストリームが出来る. 結果のストリームの各フレームに対し, フレームにある変数の値を使って, 元々の質問を具体化する. 具体化された質問のストリームが最後に印字される.74
駆動ループはまた特別なコマンドassert!もチェックする. 入力が質問ではなく, データベースに追記すべき表明や規則であることを示す. 例えば
(assert! (job (Bitdiddle Ben) (computer wizard)))
(assert! (rule (wheel ?person)
(and (supervisor ?middle-manager ?person)
(supervisor ?x ?middle-manager))))
67
マッチングは, 一般に
非常に高価なので, フルマッチャをデータベースのすべての要素に作用させるのは避けたい. 通常これはプロセスを, 高速で粗いマッチと, 最終マッチに分割して行われる. 粗いマッチはデータベースをフィルタし, 最終マッチの候補の小さい集合を作る. 粗いマッチの作業が, 候補を選ぼうとした時でなく, データベースが構築された時に出来るように注意して配置する. これをデータベースの
インデキシング(indexing)という. データベースインデキシングの方法について構築された膨大な技法がある. 4.4.4節に記述する実装は, そういう最適化の, 単純な思いつきの形になっている.
68
しかしこの種の指数的爆発は, 追加の条件が, 生成されるフレームの数を増加させるよりは, 減少させる傾向があるので, and質問ではあまりない.
69
複雑な質問の効率よい扱い方に関する, データベース管理システムの文献はたくさんある.
70
notのフィルタ実装と, 数学的論理における通常のnotの意味の間には,
微妙な相違がある. 4.4.3節参照
71
一方向性のパターンマッチでは, パターン変数を含む式は明示的で, 未知数(パターン変数)に対しては既に解かれている.
72
ユニフィケーションのもう一つの考え方は, 二つのパターンの最も一般的な特殊化を生成するということである. つまり(?x a)と((b~?y)~?z)のユニフィケーションは((b ?y) a)であり, 上で論じた(?x a ?y)と(?y ?z a)のユニフィケーションは(a a a)である. われわれの実装では, ユニフィケーションの結果はパターンよりはフレームと考えるのが便利である.
73
ユニフィケーションはマッチングの一般化なので, 両方のストリームを作り出すのに, ユニファイアを使うことでシステムを単純化出来る. しかしやさしい場合に, 単純なマッチャを使うと, (満開のユニファイアに対し)マッチングが,
それ自身として有用なことがわかる.
74
フレームに(リストでなく)
ストリームを使う理由は, 規則の再帰的作用が, 質問の満足する値を無限に作り出し得るからである. ストリームに組み込まれた遅延評価が, ここでは不可欠である. システムは応答が有限であるか無限であるかに拘らず, 出来るなり一つずつ応答を印字する.