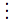⟨expn⟩)
われわれの言語の構文の仕様は次の通り:
•自己評価式は数と文字列だけである:
(define (self-evaluating? exp)
(cond ((number? exp) true)
((string? exp) true)
(else false)))
•変数は記号で表現する:
(define (variable? exp) (symbol? exp))•クォート式は(quote ⟨text-of-quotation⟩)の形である:9
(define (quoted? exp) (tagged-list? exp 'quote)) (define (text-of-quotation exp) (cadr exp))quoted?は, 指示した記号で始るリストを識別する手続きtagged-list?を使って定義する:
(define (tagged-list? exp tag)
(if (pair? exp)
(eq? (car exp) tag)
false))
•代入は(set! ⟨var⟩ ⟨value⟩)の形である:
(define (assignment? exp) (tagged-list? exp 'set!)) (define (assignment-variable exp) (cadr exp)) (define (assignment-value exp) (caddr exp))•定義は
(define ⟨var⟩ ⟨value⟩)または
(define (⟨var⟩ ⟨parameter1⟩ ... ⟨parametern⟩) ⟨body⟩)の形である. 後の形(標準手続き定義)は
(define ⟨var⟩
(lambda (⟨parameter1⟩ ... ⟨parametern⟩)
⟨body⟩))
の
構文シュガーである. 対応する構文手続きは次の通り:
(define (definition? exp)
(tagged-list? exp 'define))
(define (definition-variable exp)
(if (symbol? (cadr exp))
(cadr exp)
(caadr exp)))
(define (definition-value exp)
(if (symbol? (cadr exp))
(caddr exp)
(make-lambda (cdadr exp) ; 仮パラメタ
(cddr exp)))) ; 本体
•lambda式は記号lambdaで始るリストである:
(define (lambda? exp) (tagged-list? exp 'lambda)) (define (lambda-parameters exp) (cadr exp)) (define (lambda-body exp) (cddr exp))また上のdefinition-valueが使うlambda式の構成子も用意する:
(define (make-lambda parameters body) (cons 'lambda (cons parameters body)))•条件式はifで始り, 述語と帰結部と(場合により)代替部を持つ. 式に代替部がなければ, 代替部としてfalseを置く.10
(define (if? exp) (tagged-list? exp 'if))
(define (if-predicate exp) (cadr exp))
(define (if-consequent exp) (caddr exp))
(define (if-alternative exp)
(if (not (null? (cdddr exp)))
(cadddr exp)
'false))
またcond式をif式に変換するcond->ifに使うif式の構成子も用意する:
(define (make-if predicate consequent alternative) (list 'if predicate consequent alternative))•beginは式の並びを単一の式に包み込む. begin式から実際の並びが取れるようにbegin式の構文演算と, 並びの最初の式と残りの式を返す選択子を用意する.11
(define (begin? exp) (tagged-list? exp 'begin)) (define (begin-actions exp) (cdr exp)) (define (last-exp? seq) (null? (cdr seq))) (define (first-exp seq) (car seq)) (define (rest-exps seq) (cdr seq))(cond->ifが使う)構成子sequence->expも用意する. これは必要ならbeginを使い, 並びを単一の式に変換する:
(define (sequence->exp seq)
(cond ((null? seq) seq)
((last-exp? seq) (first-exp seq))
(else (make-begin seq))))
(define (make-begin seq) (cons 'begin seq))
•手続き作用は上の式の形のいずれでもない任意の合成式である. 式のcarが演算子, cdrが被演算子のリストである:
(define (application? exp) (pair? exp)) (define (operator exp) (car exp)) (define (operands exp) (cdr exp)) (define (no-operands? ops) (null? ops)) (define (first-operand ops) (car ops)) (define (rest-operands ops) (cdr ops))
(cond ((> x 0) x)
((= x 0) (display 'zero) 0)
(else (- x)))
の評価の問題はifとbegin式を使った次の式
(if (> x 0)
x
(if (= x 0)
(begin (display 'zero)
0)
(- x)))
の評価の問題に簡約出来る. condの評価をこのように実装すると, 評価プロセスを明確に規定しなければならない特殊形式の数が減るので, 評価器が単純になる.
cond式の要素を取り出す構文手続きと, cond式をif式に変換する手続きcond->ifを用意する. 場合分けはcondで始り, 述語と行動の節のリストを持つ. 述語が記号elseの時, 節はelse節である.12
(define (cond? exp) (tagged-list? exp 'cond))
(define (cond-clauses exp) (cdr exp))
(define (cond-else-clause? clause)
(eq? (cond-predicate clause) 'else))
(define (cond-predicate clause) (car clause))
(define (cond-actions clause) (cdr clause))
(define (cond->if exp)
(expand-clauses (cond-clauses exp)))
(define (expand-clauses clauses)
(if (null? clauses)
'false ; else節なし
(let ((first (car clauses))
(rest (cdr clauses)))
(if (cond-else-clause? first)
(if (null? rest)
(sequence->exp (cond-actions first))
(error "ELSE clause isn't last -- COND->IF"
clauses))
(make-if (cond-predicate first)
(sequence->exp (cond-actions first))
(expand-clauses rest))))))
構文変換として実装するようにした(condのような)式を導出された式(derived expressions)という. let式もまた導出された式である(問題4.6参照).13
問題 4.2
Louis Reasonerはevalの中のcond節の順序を変え, 手続き作用の節が代入の節の前に現れるようにしようと考えた. 彼はこうすると, 解釈系の効率が高まると主張した. プログラムには代入や定義などより, 手続き作用の方が多いからで, 彼は元々のevalより少ない節を調べて式の型が識別出来るようevalを修正した.
a. Louisの計画では何が悪かったか. (ヒント: 式(define x 3)に対して, Louisの評価器は何をするか.)
b.
Louisは自分の考えがうまくいかないので驚いた. 評価器が, 式の他の型の大部分を調べる前に, 手続き作用を認識するなら, プログラムがどんなに長くなっても構わなかった. 評価される言語の構文を変更し, 手続き作用がcallで始るようにして彼を助けよ. 例えば(factorial 3)の代りに, 今は(call factorial 3)と書かなければならず, (+ 1 2)の代りに,
(call + 1 2)と書かなければならない.
問題 4.3
データ主導流で振分け出来るようevalを書き直せ. これを問題2.73のデータ主導微分プログラムと比較せよ. (この節で実装した構文では, それが適切なので, 合成式のcarを式の型として使え.)
問題 4.4
1章にあった特殊形式andとorの定義を思い出そう:
and: 式を左から右へ評価する. ある式が偽に評価されたら偽を返す;
残りの式は評価しない. すべての式が真に評価されたら, 最後の式の値を返す.
式が一つもなければ真を返す.
or: 式を左から右へ評価する. ある式が真の値に評価されたらその値を返す; 残りの式は評価しない. すべての式が偽に評価されるか, 式が一つもなければ偽を返す.
適切な構文手続きと評価手続きeval-andとeval-orを作り,
andとorを評価器の新しい特殊形式として組み込め.
またandとorを導出された式として評価する方法を示せ.
問題 4.5
Schemeにはcond節にもう一つの構文(⟨test⟩
=>⟨recipient⟩)がある. ⟨test⟩が真の値に評価されると,
⟨recipient⟩が評価される. その値は一引数の手続きでなければならない;
この手続きは次に⟨test⟩の値に対して呼び出され, その結果がcond
式の値として返る. 例えば
(cond ((assoc 'b '((a 1) (b 2))) => cadr)
(else false))
は2を返す. この拡張構文が使えるよう, condの処理を修正せよ.
(let ((⟨var1⟩ ⟨exp1) ... (⟨varn⟩ ⟨expn⟩)) ⟨body⟩)は
((lambda (⟨var1⟩ ... ⟨varn⟩) ⟨body⟩) ⟨exp1⟩と等価なので, let式は導出された式である. let式の評価を上に示す型の組合せの評価に簡約する構文変換let->combinationを実装し, let式が扱えるようevalに適当な節を追加せよ.
(let* ((x 3)
(y (+ x 2))
(z (+ x y 5)))
(* x z))
は39を返す. let*式がどのように入れ子のlet式に書き直せるかを説明し, この変換を行う手続きlet*->nested-lets
を書け. letの実装が済んでいて(問題4.6), 評価器がlet*も処理出来るように拡張したければ, evalにその行動が(eval (let*->nested-lets exp) env)である節を追加するだけで十分か, それとも導出されたのでない式を使ってlet*を積極的に展開しなければならないか.
(let ⟨var⟩ ⟨bindings⟩ ⟨body⟩)⟨bindings⟩と⟨body⟩は通常のletと同じであるが, 違いは⟨var⟩が⟨body⟩の中で, 本体を⟨body⟩とし, パラメタを⟨bindings⟩の変数とする手続きに束縛されることである. そこで⟨var⟩と名前のついた手続きを呼ぶことで, ⟨body⟩を何度でも繰り返し実行することが出来る. 例えば反復的Fibonacci手続き(1.2.2節)は名前つきletを使い, 次のように書き直すことが出来る.
(define (fib n)
(let fib-iter ((a 1)
(b 0)
(count n))
(if (= count 0)
b
(fib-iter (+ a b) a (- count 1)))))
問題4.6のlet->combinationを, 名前つきletが使えるように修正せよ.
9
2.3.1節で述べたように, 評価器はクォート式を, 式が引用符を使って入力されたとしても, quoteで始るリストと見る. 例えば式'a
は評価器には(quote a)と見える. 問題2.55参照
10
述語が偽の時で代替部のないif式の値は, Schemeでは規定しない; ここではそれを偽とするように選んだ. 式の中の変数trueとfalseは, それらを大域環境で束縛し, 評価出来るような使い方を考える. 4.1.4節参照.
11
式のリストに関するこれらの選択子---
と被演算子のリストに関する対応するもの---はデータ抽象とは意図しない. それらは基本的リスト演算に対する記憶用の名前で, 5.4節の積極制御評価器の理解を容易にするものである.
12
述語がすべて偽の時でelse節のないcond式の値は,
Schemeでは規定しない; ここではそれを偽とするように選んだ.
13
実用的なLispシステムには, 評価器を修正することなく, 利用者が新しい導出された式を追加し, その実装を構文変換として指定出来る機構がある. そのような利用者定義の変換を
マクロ(macro)という. マクロを定義する初歩的な機構を追加するのは容易ではあるが, 結果の言語には名前の衝突といういやな問題がある. こういう困難を惹き起さないようなマクロ定義の機構に関して研究が多くある. 例えば
Kohlbecker 1986,
Clingerと
Rees 1991および
Hanson 1991参照.