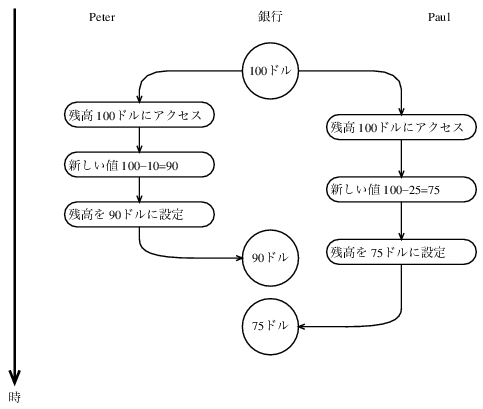
図3.29 銀行の二つの払出しの事象の順の混ざり合いが誤った最終残高になり得ることを示すタイミング図
複雑な状況下では, そういう見方は問題になる. PeterもPaulも他の人々も, 世界中に分散している銀行の現金自動預け払い機のネットワークを通して, 同じ銀行口座にアクセスしているとする. 口座の残高の実際の並びは, アクセスの細いタイミングと, 機械間の細い通信とに, 微妙に依存している.
事象の順の非決定性は, 並列システムの設計に深刻な問題を投げかける. 例えばPeterとPaulの払出しが共通変数balanceを共有し, それぞれのプロセスは3.1.1節の手続き:
(define (withdraw amount)
(if (>= balance amount)
(begin (set! balance (- balance amount))
balance)
"Insufficient funds"))
が規定する二つの別々のプロセスで実装してあるとする. 二つのプロセスが独立に実行されるならPeterは残高を調べ, 正当な金額を払い出そうとするかも知れない. しかしPeterが残高を調べた時と, Peterが払出しを終えた時の間にPaulはいくらかのお金を払い出したかも知れず, Peterのテストを無効にする.
事情はもっと悪くなり得る. 払出しのプロセスの一部で実行される式
(set! balance (- balance amount))を考えよう. これは三つのステップ: (1)balance変数の値にアクセスし; (2)新残高を計算し; (3)balanceに新しい値を設定する, で出来ている. PeterとPaulの払出しがこの文を同時に実行すれば, 二つの払出しでbalanceにアクセスし, それを新しい値に設定する順が混ざり合うかも知れない.
図3.29のタイミング図は, balanceは100ドルで始り. Peterが10ドル払い出し, Paulが25ドル払い出し, しかもbalanceの最後の値は75ドルであるという事象の順を示す. 図に示すようにこの変則の理由は, 引かれるべきbalanceの値は100ドルという仮定での, Paulの75ドルのbalance への代入である. その仮定はPeterがbalanceを90ドルに変えた時に不当になった. システムのお金の量が保存されないので, これは銀行システムとしては壊滅的な欠陥である. 取引きの前のお金の総量は100ドルであった. 後ではPeterが10ドル, Paulが25ドル, 銀行は75ドル持っている.36
ここで分る一般的現象は, 複数のプロセスが共通の状態変数を共有することがあるということだ. これを複雑にする原因は, 複数のプロセスが共有状態を同時に操作しようとすることである. 銀行口座を例にとれば, 各取引きの間, 顧客は他の顧客が存在しないかのように行動出来るべきである. 顧客が残高を,
残高に依存する方法で変える時は, 変更の瞬間の直前にも残高は考えたとおりであると仮定出来るべきである.

図3.29 銀行の二つの払出しの事象の順の混ざり合いが誤った最終残高になり得ることを示すタイミング図
並列に対する可能な制限の一つは, 共有状態変数を変更する二つの演算は同時に起きてはいけないと限定することである. しかしこれは非常に厳しい要求である. 分散銀行システムでは一時には一取引きしか働かないとシステム設計者に保証させるようなものだ. これは非能率であり, 保守的過ぎる. 図3.30はPeterとPaulが銀行口座を共有し, Paulは個人の口座も持っていることを示す.
図は共同口座から二回の払出し(Peterが一回, Paulが一回)と, Paulの個人口座への預入れを示す.38
共通口座からの二回の払出しは(同じ口座にアクセスし更新するので)並列的であってはいけないし, Paulの預入れと払出しは(Paulの財布の金額にアクセスし更新するので)並列的であってはいけない. しかしPaulが個人の口座に預け入れるのとPeterが共同口座から払い出すのが並列的に進むのを許すには何の問題もない.
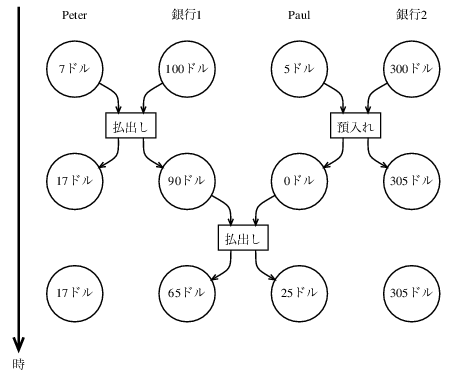
図3.30 銀行1の共同口座と銀行2の個人口座の並列預入れと払出し
並列性のもう少し厳しくない制限は, 並列システムが, プロセスがある順序で逐次的に走ったのと同じ結果を生じるように保証することである. この要請には二つの重要な点がある. 第一にプロセスが実際に逐次的に走ることを要求するのではない. それらが逐次的に走ったかのようなのと同じ結果を生じればよい. 図3.30の例で銀行口座システムの設計者はPaulの預入れとPeterの払出しが並列的に起きるのを安全に許すことが出来る. 二つの操作が逐次的に起きたのと正味の結果は同じだからである. 次に並列プログラムは「正しい」結果を一つ以上生じるかも知れない. 結果がある逐次的順と同じであることだけを要求するからである. 例えばPeterとPaulの共通口座が100ドルから始り, Peterが40ドル預け入れ, Paulが口座の金額の半分を払い出すのが並列的だったとしよう. 逐次的な実行では口座の残高は70ドルか90ドルであり得る(問題3.38参照).39
並列プログラムの正しい実行に対する更に弱い要求もある. (オブジェクト内の熱の流れのような)
拡散をシミュレートするプログラムは, それぞれが空間の小さい体積を表し,
その値を並列に更新する多数のプロセスで出来ているかも知れない. 各プロセスは, その値を自分の値と近傍の値の平均に繰り返し変更する. アルゴリズムは演算が実行される順に関係なく正しい答に収束する; 共有値の並列利用には何の制限をする必要もない.
問題 3.38
Peter, PaulとMaryが最初100ドルあった共同銀行口座を共有していたとする. 次の命令で並列的にPeterは10ドル預け入れ, Paulは20ドル払い出し,
Maryは口座の金額の半分を払い出す:
| Peter: | (set! balance (+ balance 10)) |
| Paul: | (set! balance (- balance 20)) |
| Mary: | (set! balance (- balance (/ balance 2))) |
35
ケンブリッジの建物の壁の落書から引用すると,
「時は事が同時に置きないように発明された仕掛けである」
36
システムに更に悪い欠陥が起きるのは, 二つのset!が残高を同時に変えようとすることで, その場合, 記憶場所に見られるデータは, 二つのプロセスの書いた情報のランダムな組合せになったりするだろう. 殆んどの計算機には, 基本の記憶装置書込み命令はインターロックを持ち, 同時のアクセスを防ごうとする.
この見た目に単純な保護でも, マルチプロセス計算機の設計に実装上のチャレンジをもたらし, メモリーアクセスの速度を上げるため, 異る処理装置の間でデータが複製され(「キャッシュ」され)ているにも拘らず, 各処理装置で記憶装置の内容の一貫性ある見え方を持ち得るよう, 巧妙な
キャッシュコヒーレンス(cache-coherence)プロトコルが必要となる.
37
3.1.3節の階乗プログラムが, 単一逐次プロセスでの例を示す.
38
縦の列は, 払出しと預入れの前後の, Peterの財布, (銀行1の)共同口座, Paulの財布, (銀行2の)Paulの口座を示す. Peterは銀行1から10ドルを払い出し, Paulは銀行2に5ドルを預け入れ, 次に銀行1から25ドルを払い出した.
39
この考えを表すより形式的な方法は, 並列的プログラムは本来
非決定的(nondeterministic)であるということだ. つまり一価関数ではなく, その結果が可能性のある値の集りであるような関数で記述される. 4.3
節で非決定的計算を表す言語を学ぶ.