[ 目次, 前節, 次節, 索引 ]

(define (square x)
  (* x x))

(define (sum-of-squares x y)
  (+ (square x) (square y)))

(define (f a)
  (sum-of-squares (+ a 1) (* a 2)))

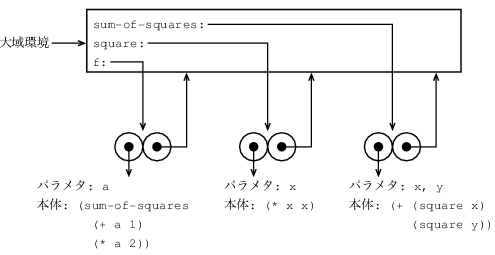
   図3.5は式(f 5)を評価して作り出される環境である. fの呼出しは新しい環境E1を作り出し, 最初のフレームにfの仮パラメタaが引数5と束縛されている. E1でfの本体

(sum-of-squares (+ a 1) (* a 2))

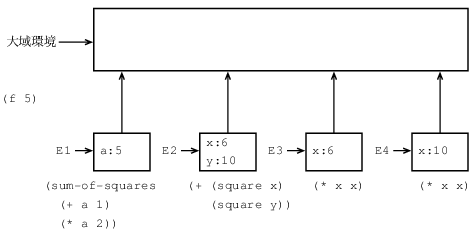
   次に手続きオブジェクトsum-of-squaresを引数6と10に作用させる. そこで新しい環境E2が出来, 仮パラメタxとyが引数に束縛される. E2の中で組合せ(+ (square x) (square y))を評価する. そこで(square x)の評価に行くが, そこではsquareは大域フレームの中で見つかり, xは6である. もう一度新しい環境E3を用意し, そこでx は6に束縛され, この中でsquareの本体, つまり(* x x)を評価する. またsum-of-squaresの作用の一部にyを10として, 式(square y)も評価しなければならない. squareの二度目の呼出しは, もう一つの環境E4を作り出し, squareの仮パラメタxは10に束縛される. E4の中で(* x x)を評価する.

   注意すべき重要な点は, squareの呼出し毎にxの束縛を含んだ新しい環境が作り出されることである. ここで別々のフレームがすべてx という名前の別々の局所変数を分けておくのに役立つことが分る. square手続きオブジェクトが表示した環境が大域環境なので, square が作り出した各フレームが大域環境を指していることに注意しよう.

   部分式が評価されると結果が戻される. squareの二度の呼出しで生成された値はsum-of-squaresで足され, この結果がfにより返される. ここでのわれわれの焦点は, 環境構造なので, 返された値がどう呼出しから呼出しへ渡されるかには, 立ち止らないが, これもまた評価プロセスの重要な点で, 5章でその細部へ戻ることにしよう.

問題 3.9

1.2.1節で階乗を計算する手続きの再帰版

(define (factorial n)
  (if (= n 1)
      1
      (* n (factorial (- n 1)))))

(define (factorial n)
  (fact-iter 1 1 n))

(define (fact-iter product counter max-count)
  (if (> counter max-count)
      product
      (fact-iter (* counter product)
                 (+ counter 1)
                 max-count)))

14 環境モデルでは, 解釈系はfact-iterのような手続きが末尾再帰を使って一定量のスペースで実行出来るという, 1.2.1節の主張は明らかでない. 末尾再帰については, 5.4節で解釈系の制御構造を扱った時に, 論じることにする.

[ 目次, 前節, 次節, 索引 ]