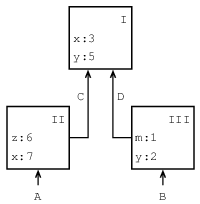
図3.1 単純な環境構造
われわれのプログラム言語に代入を一旦認めると, このような定義は最早適切でない. 特に3.1.3節で論じたように, 代入が存在すると変数はもう単に値に対する名前とは考えられない. むしろ変数は値が格納される「場所」を指示しなければならない. 評価の新しいモデルでは, これらの場所は 環境(environments)という構造の中に確保される.
環境は
フレーム(frames)の並びである. 各フレームは
束縛(bindings)の(空かも知れぬ)表である. 束縛は変数名とその値を対応づける. (一個のフレームはある変数について高々一つの束縛を持つ.) 各フレームは, それが議論のために
大域(global)であると考えられるものを除き,
外側の環境(enclosing environment)へのポインタを持つ. ある環境について,
変数の値(value of a variable)は, 環境でその変数の束縛を含んでいる最初のフレームでの変数の束縛で与えられる値である. フレームの並びのどれもがその変数の束縛を規定しなければ, その変数はその環境で
未束縛(unbound)という.

図3.1 単純な環境構造
図3.1は, I, IIおよびIIIとラベルした三つのフレームからなる単純な環境の構造を示す. A, B, CおよびDは環境へのポインタである. CとDは同じ環境を指す. 変数zとxはフレームIIで, またyとxはフレームIで束縛されている. 環境Dでのxの値は3である. 環境Bに関してxの値もまた3である. これは次のように決められる: まず並びの最初のフレーム(フレームIII)を調べる. そしてxの束縛が見つからない. そこで外側の環境Dへ進み, フレームIで束縛を見つける. 他方, 環境Aでのxの値は7である. それは並びの最初のフレーム(フレームII)がxの7への束縛を含むからだ. 環境Aに関して, フレームIIのxの7への束縛はフレームIの xの3への束縛を 隠す(shadow)という.
環境は, 式の評価される文脈を決定するので, 評価のプロセスにとって重要である. 実際プログラム言語の中の式は, それ自身では何の意味も持たないといってよいだろう. むしろ式はそれが評価される, ある環境との関りでのみ意味を獲得するのである. (+ 1 1)のような直截な式の解釈でさえ, +は加算の記号であるという文脈で演算しているという理解に依存している. このように評価のモデルでは, ある環境に関して式を評価すると, 常にいうことにする. 解釈系との関りでは, そこには
大域環境があると考える. それは唯一のフレームからなり(外側の環境はなく),
基本手続きと対応づけられた記号に対する値だけを含む. 例えば+が加算の記号だという考えは, 大域環境の中で記号+は基本加算手続きに束縛しているということで得られる.