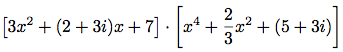
のような異る型の係数の多項式の演算が自動的に出来るようになる.
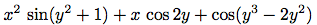
ここで完全な代数処理システムを開発するわけではない. それは相当に複雑で, 代数の深い知識と優れたアルゴリズムを必要とする. ここでは代数操作の単純だが重要な部分: 多項式の算術演算を見ることにする. そういうシステムの設計者が直面する種々の決定と, この作業を行うのに役立つ抽象データと汎用演算の考え方をどう使うか見ることにする.
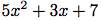
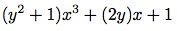
われわれは既に難しい論点に出会っている. 上の第一の多項式は, 多項式5y2 + 3y + 7と同じであるかないか. 合理的な答は「多項式を純粋に数学的関数と考えればイエスだが, 多項式を構文形式と考えればノー」である. 第二の多項式は代数的にはxの多項式を係数とするyの多項式と等価である. われわれのシステムはこれを認識すべきかどうか. その上, 多項式には他の表現法もある. ---例えば因子の積として, あるいは(一元多項式では)根の集合として, あるいは指定されたいくつかの点での多項式の値のリストとして.55 これらの疑問を巧みに解くには, われわれの代数処理システムで, 「多項式」は特定の構文形式であり, 基盤の数学的意味ではないと決めることである.
多項式の算術演算をするのにどうしたらよいか考えなければならない. この単純なシステムでは, 加算と乗算だけ考えよう. 更に組み合せる二つの多項式は同じ不定元を持っているものに限ろう.
システムの設計は, データ抽象の使い慣れた考え方でいくことにしよう. 多項式は 多項式型(poly)というデータ構造で表現するが, それは 変数と項の集りから出来ている. 多項式型からこれらの部分を取り出す選択子variableとterm-listと, 変数と項リストから多項式型を作る構成子make-polyがあると仮定する. 変数は単に記号であり, 変数を比べるのに2.3.2節の same-variable?手続きを使うことが出来る. 次の手続きは多項式型の加算と乗算を定義する:
(define (add-poly p1 p2)
(if (same-variable? (variable p1) (variable p2))
(make-poly (variable p1)
(add-terms (term-list p1)
(term-list p2)))
(error "Polys not in same var -- ADD-POLY"
(list p1 p2))))
(define (mul-poly p1 p2)
(if (same-variable? (variable p1) (variable p2))
(make-poly (variable p1)
(mul-terms (term-list p1)
(term-list p2)))
(error "Polys not in same var -- MUL-POLY"
(list p1 p2))))
多項式をわれわれの汎用算術演算システムに組み込むには型タグをつける必要がある. タグpolynomialを使うこととし, 演算表のタグつき多項式に適切な演算を設定しよう. プログラムをすべて2.5.1節のように, 多項式パッケージの設定手続きに組み込む.
(define (install-polynomial-package)
;; 内部手続き
;; 多項式型の表現
(define (make-poly variable term-list)
(cons variable term-list))
(define (variable p) (car p))
(define (term-list p) (cdr p))
⟨2.3.2節の手続きsame-variable?とvariable?⟩
;; 項と項リストの表現
⟨以下の本文にある手続きadjoin-term ...coeff⟩
(define (add-poly p1 p2) ...)
⟨add-polyが使う手続き⟩
(define (mul-poly p1 p2) ...)
⟨mul-polyが使う手続き⟩
;; システムの他の部分とのインターフェース
(define (tag p) (attach-tag 'polynomial p))
(put 'add '(polynomial polynomial)
(lambda (p1 p2) (tag (add-poly p1 p2))))
(put 'mul '(polynomial polynomial)
(lambda (p1 p2) (tag (mul-poly p1 p2))))
(put 'make 'polynomial
(lambda (var terms) (tag (make-poly var terms))))
'done)
多項式の加算は項毎に実行する. 同じ次数の(つまり不定元が同じべきを持っている)項が組み合される. これは同じ次数の新しい項を, その係数が足される項の係数の和になるように作る. もう一方の加数の同じ次数の項のない加数一つの項は, 構成される和の多項式に単に組み入れられるだけである.
項リストを操作するのに, 空の項のリストを返す構成子 the-empty-term-list, 新しい項を項リストに追加する構成子 adjoin-termがあると仮定する. また与えられた項リストが空かどうか調べる述語 empty-termlist?, 項リストの最高次の項を取り出す選択子 first-term, 最高次の項を除いたすべてを返す選択子 rest-termsがあると仮定する. 項を操作するのに次数と係数から項を構成する構成子 make-term, 項からそれぞれの次数と係数を返す選択子 orderと coeffがあると考えよう. これらの演算により, 項や項リストはデータ抽象と考えることが出来, その具体的表現はまた別に心配する.
この手続きは, 二つの多項式の和の項リストを構成する:56
(define (add-terms L1 L2)
(cond ((empty-termlist? L1) L2)
((empty-termlist? L2) L1)
(else
(let ((t1 (first-term L1)) (t2 (first-term L2)))
(cond ((> (order t1) (order t2))
(adjoin-term
t1 (add-terms (rest-terms L1) L2)))
((< (order t1) (order t2))
(adjoin-term
t2 (add-terms L1 (rest-terms L2))))
(else
(adjoin-term
(make-term (order t1)
(add (coeff t1) (coeff t2)))
(add-terms (rest-terms L1)
(rest-terms L2)))))))))
ここで注意すべき最も重要なのは, 組み合せるべき項の係数を足すのに, 汎用加算手続き
addを使ったことである. これは後で見るように強い影響力を持つ.
二つの項リストを掛けるには, 第一のリストの各項に, もう一方のリストを, 一つの項に項リストのすべての項を掛けるmul-term-by-all-termsを使って繰り返し掛ける. (第一のリストの各項について一つずつの)結果の項リストは,和に足し込まれる. 二つの項を掛けると因子の次数の和の次数で, 因子の係数の積の係数を持つ項が出来る:
(define (mul-terms L1 L2)
(if (empty-termlist? L1)
(the-empty-termlist)
(add-terms (mul-term-by-all-terms (first-term L1) L2)
(mul-terms (rest-terms L1) L2))))
(define (mul-term-by-all-terms t1 L)
(if (empty-termlist? L)
(the-empty-termlist)
(let ((t2 (first-term L)))
(adjoin-term
(make-term (+ (order t1) (order t2))
(mul (coeff t1) (coeff t2)))
(mul-term-by-all-terms t1 (rest-terms L))))))
多項式の加算と乗算に必要なものはこれだけだ.
汎用手続きaddとmulを使って項を計算するので, われわれの多項式パッケージは自動的に, 汎用算術演算パッケージが知っている型の係数を扱うことが出来る. 2.5.2節で論じたような
強制型変換機構を組み込むと
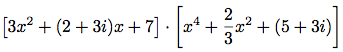
のような異る型の係数の多項式の演算が自動的に出来るようになる.
多項式の加算と乗算手続きadd-polyおよびmul-polyを汎用算術演算システムに型polynomialのaddとmul演算として設定したので, われわれのシステムは
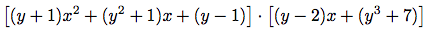
のような多項式演算を自動的に扱うことが出来る. その理由はシステムが係数を組み合せようと試みる時, addとmulが振り分けるからである. 係数それ自身は(yの)多項式なので, これらはadd-polyとmul-polyを使って組み合される. 結果は一種の
「データ主導再帰」であって, そこでは例えばmul-polyを呼び出すと係数を掛けるため, 再帰的にmul-polyが呼び出される. (三変数の多項式を表現するのに使われるように)係数の係数が多項式なら, データ手動がシステムをもう一レベルの再帰呼出しに従わせ, データの構造が命ずるままに十分なレベルまで演算が行われる.57
項リストを表現するリストをどう構造化すべきか. 一つの考えは操作しようとする多項式の「濃度」である. 多項式は殆んどの次数の項で非零の係数を持つ時,
濃い(dense)といい, 多くの零の項を持てば,
薄い(sparse)という. 例えば
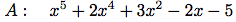
は濃い多項式であり, 一方
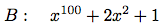
は薄い.
濃い多項式の項リストは係数のリストとして最も効率良く表現される. 例えば上のAは(1 2 0 3 -2 -5)とうまく表現出来るであろう. この表現の項の次数は, その項の係数から始まる部分リストの長さ引く1である.58 これはBのような薄い多項式にとっては恐ろしい表現である: わずかな淋しい非零項で区切られた長大な零のリストになるであろう. 薄いリストのより合理的な表現は, 各項が, 項の次数とその次数の係数を含むリストであるような非零項のリストである. この方法では多項式Bは((100 1) (2 2) (0 1))と効率よく表現される. 殆んどの多項式処理は薄い多項式についてだから, この方法を使う. 項リストは高次から低次へ配列された項のリストとして表現する. 一旦この決定をしてしまうと, 項と項リストに対する選択子の実装は直截である: 59
(define (adjoin-term term term-list)
(if (=zero? (coeff term))
term-list
(cons term term-list)))
(define (the-empty-termlist) '())
(define (first-term term-list) (car term-list))
(define (rest-terms term-list) (cdr term-list))
(define (empty-termlist? term-list) (null? term-list))
(define (make-term order coeff) (list order coeff))
(define (order term) (car term))
(define (coeff term) (cadr term))
ここで=zero?は問題2.80で定義した通りである. (次の問題2.87も参照)
多項式パッケージの利用者は(タグつけられた)多項式を手続き:
(define (make-polynomial var terms) ((get 'make 'polynomial) var terms))を使って作り出す.
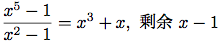
add-poly, mul-polyにならってdiv-polyを設計出来る. 手続きは二つの多項式が同じ変数を持つか調べる. そうであればdiv-poly は変数を剥し, 問題をdiv-termsに送る. それが項リストについて除算を行う. div-polyは最後にdiv-termsから貰った結果に変数を取りつける. div-termsを除算の商と剰余の両方を計算するように設計すると便利である. div-termsは引数として二つの項リストをとり, 商の項リストと剰余の項リストのリストを返す.
次のdiv-termsの定義を欠けている式を補って完成せよ. これを使って, 引数として二つの多項式型をとり, 商と剰余の多項式型のリストを返すdiv-polyを実装せよ.
(define (div-terms L1 L2)
(if (empty-termlist? L1)
(list (the-empty-termlist) (the-empty-termlist))
(let ((t1 (first-term L1))
(t2 (first-term L2)))
(if (> (order t2) (order t1))
(list (the-empty-termlist) L1)
(let ((new-c (div (coeff t1) (coeff t2)))
(new-o (- (order t1) (order t2))))
(let ((rest-of-result
⟨結果の残りを再帰的に計算する.⟩
))
⟨完全な結果を形成する.⟩
))))))
他方, 多項式代数は, データ型が自然には塔に配置出来ないシステムである. 例えば係数がyの多項式であるxの多項式を作ることが出来る. また係数がxの多項式であるyの多項式も作ることが出来る. これらの型のいずれも, 自然にはもう一方の「上に」はいない. しかしそれぞれの集合からの要素を加算することがしばしば必要になる. いくつかの方法がある. 一つの方法は, 項を展開し, 再配置し, 両方の多項式が同じ主変数を持つようにして, 一つの多項式をもう一つの型に変換するのである. 変数を順序づける, つまり常に多項式を高優先度の変数を目立たせ, 低優先度の変数を係数に埋め込み, 多項式を 「標準形」に変換することで, この上に塔状の構造を作ることが出来る. この戦略はかなりうまくいくが, 変換は多項式を無駄に展開し, 読むのを困難にし, 作業効率を落す. 塔の戦略はこの分野や, また利用者が三角関数, べき級数, 積分のように, いろいろ組み合せて古い型を使い, 新しい型を動的に発明する分野では自然でない.
強制型変換の制御が, 大規模代数処理システムの設計で重要な問題であることは驚くに当らない. こういうシステムの複雑さの多くは, 多様な型の間の関係によるものである. 実際われわれはまだ強制型変換を完全には理解していないといってよいであろう. 実はわれわれはデータ型の考え方も十分には理解していない. それでもわれわれの知識は巨大システムの設計を支える強力な構造化と部品化の原則をもたらせてくれる.
問題 2.92
変数に順序をつけることで, 多項式パッケージを拡張し, 異る変数の多項式に対しても多項式の加算と乗算が出来るようにせよ. (易しくはない)
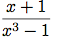
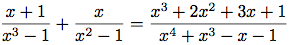
有理数算術演算パッケージを修正し, 汎用演算が使えるようにすると, 分数を最低の項まで引き下げる問題を除き, やりたいことは出来るようになる.
問題 2.93
有理数演算パッケージを汎用演算を使うように修正せよ. make-ratを変更し分数を最低の項まで引き下げようとしないようにせよ. そのシステムを二つの多項式についてmake-rationalを呼び出し, 有理関数を作ってテストせよ.
(define p1 (make-polynomial 'x '((2 1)(0 1)))) (define p2 (make-polynomial 'x '((3 1)(0 1)))) (define rf (make-rational p2 p1))さてaddを使ってrfに自分自身を足せ. この加算手続きは分数を最低項まで引き下げないことを見よ.
整数の時に使ったのと同じ考えで, 分子と分母をその最大公約数で割るように修正して, 多項式分数を最低項へ引き下げることが出来る. 「最大公約数」は多項式にも意味がある. 実際, 整数に働くEuclidアルゴリズムと実質的に同じものを使って二つの多項式のGCDが計算出来る.60 整数版は
(define (gcd a b)
(if (= b 0)
a
(gcd b (remainder a b))))
これを使って多項式リストに働くGCD演算を定義するため自明な修正をする.
(define (gcd-terms a b)
(if (empty-termlist? b)
a
(gcd-terms b (remainder-terms a b))))
ここでremainder-termsは問題2.91で実装した項リスト除算演算div-termsの返したリストから, 剰余の部分を取り出す.
(define p1 (make-polynomial 'x '((4 1) (3 -1) (2 -2) (1 2)))) (define p2 (make-polynomial 'x '((3 1) (1 -1)))) (greatest-common-divisor p1 p2)を試み, 結果を手計算で調べよ.
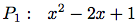
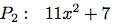
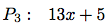
問題2.95の示した問題はGCDアルゴリズムに(整数係数の多項式の場合にしか動かない)次の修正をすれば解決出来る. GCD計算で多項式除算を実行する前に, 除算の最中に分数が現れないことを保証するように選んだ整定数を被除数に掛ける. 答はそれで実際のGCDより整定数倍だけ違うが, 有理関数を最低の項まで引き下げる場合には問題ない: このGCDは分子と分母の両方を割るのに使うから, 整数倍は打ち消し合う.
より正確には, PとQを多項式とし, O1をPの次数(Pの最高項の次数)
, O2をQの次数とする. cをQの先頭の係数とする. Pに
整数化因子(integerizing factor) c1+O1-O2を掛けると, 結果の多項式はdiv-termsアルゴリズムを使うと, 分数を持ち込むことなく,
Qで割り切ることが示せる. 被除数にこの定数を掛け, 次に割る計算はPのQによる
擬除算(pseudodivision)ということがある. この除算の剰余は擬剰余
(pseudoremainder)という.
問題 2.96
a. div-termsを呼び出す前に上に述べた整数化因子を被除数に掛けることの他はremainder-termsと同じである手続きpseudoremainder-termsを実装せよ. gcd-termsを修正し,
pseudoremainder-termsを使うようにし, greatest-common-divisor
は今では, 問題2.95の例でも整数係数を持つ答が生成出来ることを調べよ.
b. GCDは今や整数係数を持つ. しかしそれはP1のより大きい.
gcd-termsを変更し, 全係数を(整数の)最大公約数で割ることで, 答の整数から共通因子を除け.
これが有理関数を最低の項まで引き下げる方法である:
•gcd-termsの問題2.96の版を使い, 分子と分母のGCDを計算する.
•GCDを得たら, GCDで割る前に, 非整数係数を持ち込まないように,
分子と分母に同じ整数化因子を掛ける. 使える因子としては, GCDの第一係数を1 + O1 - O2乗する. ここでO2はGCDの次数, O1は分子と分母の次数の大きい方である. これは分子, 分母をGCDで割っても, 分数は出てこないことを保証する.
•この演算の結果は, 整数係数を持つ分子と分母である. 係数は, すべての整数化因子のせいで通常非常に大きい. そこで最後の段階は, 分子と分母の全係数の(整数)最大公約数を計算し, それで割り, 冗長な因子を取り除く.
問題 2.97
a. このアルゴリズムを, 二つの項リストnとdを引数としてとり,
上のアルゴリズムにより, nとdが最低項まで引き下げられたリストnnとddを返す手続きreduce-termsとして実装せよ.
add-polyに似た手続きreduce-polyを書け. それは二つの多項式型が同じ変数を持つか調べ, 同じ変数ならreduce-polyは変数を剥し, 問題をreduce-termsに渡し, reduce-termsから返された二つの項リストに変数を再び取りつける.
b. reduce-termsに似た, 元々のmake-ratが整数に対して行ったようなことをする手続きを定義せよ.
(define (reduce-integers n d)
(let ((g (gcd n d)))
(list (/ n g) (/ d g))))
そしてapply-genericを呼び出して, (polynomial引数なら)
reduce-polyへ, (scheme-number引数なら)
reduce-integerへ振り分ける手続きreduceを汎用演算として定義せよ. こうして有理数演算パッケージに, make-ratに分子と分母を結合して有理数を作る前に, reduceを呼び出させることで, 分数を最低の項まで引き下げさせることが出来る. このシステムは今では整数でも多項式でも有理式を扱うことが出来る. プログラムをテストするのに, この拡張問題の最初の例を試みよ.
(define p1 (make-polynomial 'x '((1 1)(0 1)))) (define p2 (make-polynomial 'x '((3 1)(0 -1)))) (define p3 (make-polynomial 'x '((1 1)))) (define p4 (make-polynomial 'x '((2 1)(0 -1)))) (define rf1 (make-rational p1 p2)) (define rf2 (make-rational p3 p4)) (add rf1 rf2)最低の項まで正しく引き下げられている正しい答を得たか調べよ.
GCD計算は, 有理関数の演算を行うシステムの中心にある. 上で使ったアルゴリズムは数学的に直截であるが, 非常に遅い. この遅さは部分的には除算の回数の多さにより, また部分的には, 擬除算によって生成された中間の係数の巨大さによる. 代数処理システム開発の活動分野の一つは, 多項式GCD計算のよりよいアルゴリズムの設計である.62
54
他方で係数がそれ自体, 他の変数の多項式である多項式は許すことにする. これにより本質的には多元システムと同じ表現力を持つことが出来るが,
後で論じるように強制型変換の問題が出てくる.
55
一元多項式では, 与えられた点の集合での多項式の値を与えることは,
特に良好な表現である. これは多項式算術演算を非常に単純にする. この方法で表現された二つの多項式の和を求めるには, 対応する点の多項式の値を足すだけでよい. よく見なれた表現に直すには, n + 1個の点における多項式の値からn次の多項式の係数を求める
Lagrangeの内挿公式を使うことが出来る.
56
この演算は問題2.62で開発した順序づけられたunion-set演算と非常によく似ている.
実際多項式の項を不定元の次数に従って順序づけられた集合と考えれば, 和の項リストを作るプログラムはunion-setと殆んど同じである.
57
これが完全に円滑に行われるためには,
汎用算術演算システムに「数」を係数がその数である零次の多項式として, 多項式への強制型変換の機能を加えよう. これは
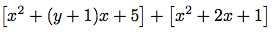
のように係数y + 1を係数2に足さなければならない演算を実行する時に必要である.
58
これらの多項式の例では, 問題2.78で示した型機構を使った汎用算術演算システムが実装してあると仮定する. だから通常の数の係数は, (carが記号scheme-numberである対ではなく,) 数それ自身として表現される.
59
項リストは順序づけられていると仮定しているが, adjoin-termは新しい項を既存の項リストに単にconsするよう実装した. adjoin-termを使う(add-termsのような)手続きが常にリストに現れるのより高次の項を持って呼び出されると保証出来るなら, これで済ますことが出来る. そういう保証がしたくなければadjoin-termを順序づけられたリストの表現(問題2.61)のadjoin-set構成子に似た方法で実装していたであろう.
60
Euclidのアルゴリズムが多項式にも働くのは, 代数では多項式は
Euclid環という代数領域の一種を形成するということで形式化される.
Euclid環は環の各要素xに正整数「測度」m(x)を代入する加算, 減算および交換可能な乗算を認める領域である. 任意の非零xとyについてm(xy)≥m(x)であり, 任意のx, yについて, y = qx +rでかつr = 0
かm(r) < m(x)なるqが存在する. 抽象的観点からは, Euclidアルゴリズムが働くことを証明するのに必要なものである. 整数の領域では, 整数の測度mは整数自身の絶対値である. 多項式の領域では, 多項式の次数である.
61
MIT Schemeの実装では, 実際にQ1とQ2の有理係数のついた除数である多項式を計算する. 他の多くのSchemeシステムでは, 整数の除算が有限精度の十進数を生成するので, 正しい除数が得られないかも知れない.
62
多項式GCD計算の非常に効率のよい, きれいな方法は
Richard Zippel(1979)が発見した. この方法は1章で議論した, 素数性の高速テストのような, 確率アルゴリズムである. Zippelの本(1993)にはその方法と,
他の多項式GCD計算の方法が述べてある.