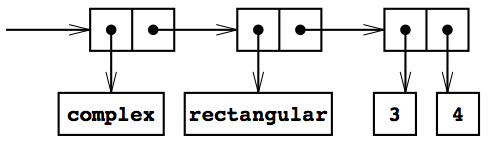
図2.24 直交座標形式での3 + 4iの表現
汎用算術演算手続きを次のように定義する:
(define (add x y) (apply-generic 'add x y)) (define (sub x y) (apply-generic 'sub x y)) (define (mul x y) (apply-generic 'mul x y)) (define (div x y) (apply-generic 'div x y))
通常(ordinary)の, つまりわれわれの言語に基本の数を扱うパッケージの設定から始める. これらに記号scheme-numberのタグをつける. このパッケージの算術演算は基本の算術演算手続きである. (だからタグをはずした数を扱う手続きを定義する必要はない.) これらの演算は二つの引数をとるので, 表にはリスト(scheme-number scheme-number)のキーで設定する:
(define (install-scheme-number-package)
(define (tag x)
(attach-tag 'scheme-number x))
(put 'add '(scheme-number scheme-number)
(lambda (x y) (tag (+ x y))))
(put 'sub '(scheme-number scheme-number)
(lambda (x y) (tag (- x y))))
(put 'mul '(scheme-number scheme-number)
(lambda (x y) (tag (* x y))))
(put 'div '(scheme-number scheme-number)
(lambda (x y) (tag (/ x y))))
(put 'make 'scheme-number
(lambda (x) (tag x)))
'done)
Scheme数パッケージの利用者は, (タグつきの)通常の数を手続き:
(define (make-scheme-number n) ((get 'make 'scheme-number) n))を使って作り出す.
汎用算術演算システムの枠組が出来たので, 次の種類の数を取り込もう. これは有理数算術演算を実行するパッケージである. 加法性のおかげで, 2.1.1節の有理数のプログラムを, このパッケージの内部手続きとして, 修正なしに使うことが出来る:
(define (install-rational-package)
;; 内部手続き
(define (numer x) (car x))
(define (denom x) (cdr x))
(define (make-rat n d)
(let ((g (gcd n d)))
(cons (/ n g) (/ d g))))
(define (add-rat x y)
(make-rat (+ (* (numer x) (denom y))
(* (numer y) (denom x)))
(* (denom x) (denom y))))
(define (sub-rat x y)
(make-rat (- (* (numer x) (denom y))
(* (numer y) (denom x)))
(* (denom x) (denom y))))
(define (mul-rat x y)
(make-rat (* (numer x) (numer y))
(* (denom x) (denom y))))
(define (div-rat x y)
(make-rat (* (numer x) (denom y))
(* (denom x) (numer y))))
;; システムの他の部分へのインターフェース
(define (tag x) (attach-tag 'rational x))
(put 'add '(rational rational)
(lambda (x y) (tag (add-rat x y))))
(put 'sub '(rational rational)
(lambda (x y) (tag (sub-rat x y))))
(put 'mul '(rational rational)
(lambda (x y) (tag (mul-rat x y))))
(put 'div '(rational rational)
(lambda (x y) (tag (div-rat x y))))
(put 'make 'rational
(lambda (n d) (tag (make-rat n d))))
'done)
(define (make-rational n d)
((get 'make 'rational) n d))
タグcomplexを使い, 複素数を扱う同様なパッケージが設定出来る. このパッケージを作るのに, われわれは表から, 直交座標と極座標パッケージで定義された演算make-from-real-imagとmake-from-mag-angを取り出す. 加法性により, 内部手続きとして2.4.1節のadd-complex, sub-complex, mul-complexおよびdiv-complexを使うことが出来る.
(define (install-complex-package)
;; 直交座標と極座標パッケージから取り入れた手続き
(define (make-from-real-imag x y)
((get 'make-from-real-imag 'rectangular) x y))
(define (make-from-mag-ang r a)
((get 'make-from-mag-ang 'polar) r a))
;; 内部手続き
(define (add-complex z1 z2)
(make-from-real-imag (+ (real-part z1) (real-part z2))
(+ (imag-part z1) (imag-part z2))))
(define (sub-complex z1 z2)
(make-from-real-imag (- (real-part z1) (real-part z2))
(- (imag-part z1) (imag-part z2))))
(define (mul-complex z1 z2)
(make-from-mag-ang (* (magnitude z1) (magnitude z2))
(+ (angle z1) (angle z2))))
(define (div-complex z1 z2)
(make-from-mag-ang (/ (magnitude z1) (magnitude z2))
(- (angle z1) (angle z2))))
;; システムの他の部分へのインターフェース
(define (tag z) (attach-tag 'complex z))
(put 'add '(complex complex)
(lambda (z1 z2) (tag (add-complex z1 z2))))
(put 'sub '(complex complex)
(lambda (z1 z2) (tag (sub-complex z1 z2))))
(put 'mul '(complex complex)
(lambda (z1 z2) (tag (mul-complex z1 z2))))
(put 'div '(complex complex)
(lambda (z1 z2) (tag (div-complex z1 z2))))
(put 'make-from-real-imag 'complex
(lambda (x y) (tag (make-from-real-imag x y))))
(put 'make-from-mag-ang 'complex
(lambda (r a) (tag (make-from-mag-ang r a))))
'done)
複素数パッケージ外のプログラムは, 実部と虚部とから, または絶対値と偏角とから複素数を構成することが出来る. 元々直交座標や極座標パッケージで定義した基盤になる手続きが, 複素数パッケージへ持ち出され, 更に外の世界に持ち出される方法に注意しよう.
(define (make-complex-from-real-imag x y) ((get 'make-from-real-imag 'complex) x y)) (define (make-complex-from-mag-ang r a) ((get 'make-from-mag-ang 'complex) r a))
ここにあるのは二レベルのタグシステムで, 直交座標の3 + 4iのような普通の複素数は図2.24のように表現される. 外側のタグ(complex)は数を複素数パッケージへ導くのに使われる. 複素数パッケージに入れば次のタグ(rectangular)が数を直交座標パッケージへ導くのに使われる. 大きく複雑なシステムでは, 多くのレベルがあり, 各レベルが汎用演算により次のシステムとインターフェースをとる. データオブジェクトが「下方へ」渡されるにつれ,
適切な手続きへ導くのに使われた外方のタグは, (contentsを作用させて)剥され, 次のレベルのタグが(あるなら)更なる振分けに使えるよう, 見えてくる.

図2.24 直交座標形式での3 + 4iの表現
上のパッケージで, add-ratやadd-complexや他の算術演算の手続きは, 元々書いた通りに使った. しかしこれらの定義が異る実装手続きの内部になると, それらは相互に違う名前である必要はない: それらのパッケージの中で, 単にadd, sub, mulおよびdivと名づけることが出来る.
問題 2.77
Louis Reasonerはzを図2.24に示すオブジェクトとして, 式(magnitude z)を評価しようとした. 驚いたことに答の5の代りに, 型(complex)には演算magnitudeは対応する手続きはないというapply-genericのエラーメッセージを得た. この対話をAlyssa P. Hackerに見せると, 彼女は「complex数に対して複素数の選択子は定義されていず,
polarとrectangularだけ定義されているのが問題である. これが働くようにするには, complexパッケージに次のものを追加しなければならない」という:
(put 'real-part '(complex) real-part) (put 'imag-part '(complex) imag-part) (put 'magnitude '(complex) magnitude) (put 'angle '(complex) angle)どうしてこれが働くか詳しく述べよ. 例えばzが図2.24に示すオブジェクトとして, 式(magnitude z)を評価する時, 呼び出されるすべての手続きをトレースせよ. 特にapply-genericは何回呼び出されるか. それぞれの場合どの手続きが振り分けられるか.