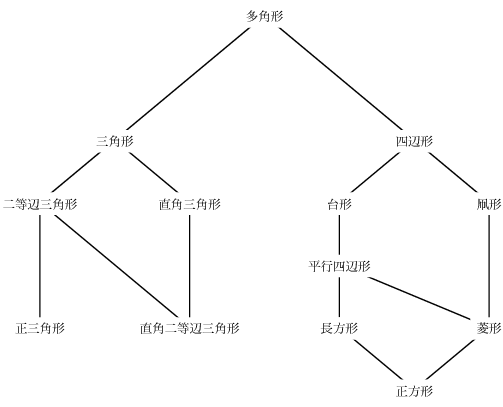
図2.26 幾何学図形の型の間の関係
型の間の演算を扱う一つの方法は, 演算が許されている型の組合せ毎に別の手続きを設計することである. 例えば複素数パッケージを拡張し, 複素数を通常の数に足す手続きを用意し, これをタグ(complex scheme-number)を使って設定するのである:49
;; 複素数パッケージに組み込まれる.
(define (add-complex-to-schemenum z x)
(make-from-real-imag (+ (real-part z) x)
(imag-part z)))
(put 'add '(complex scheme-number)
(lambda (z x) (tag (add-complex-to-schemenum z x))))
この技法はうまくいくが煩わしい. こういうシステムでは, 新しい型を導入するコストは, その型のパッケージを構成するだけでなく, 型の間の演算を実装する手続きの構成と設定にある. これは型自体の演算を定義するのに必要なプログラムを簡単に越えてしまう. この方法はまたわれわれの別々のパッケージを加法的に組み合せる能力を危うくし, 少なくとも個々のパッケージの実装者が, 他のパッケージに対して注意を払う限度を制限する能力を危うくする. 例えば上の例では, 複素数と通常の数の混合演算を扱うのが, 複素数パッケージの責任なのは合理的に思える. しかし有理数と複素数の統合は, 複素数パッケージか, 有理数パッケージか, 二つのパッケージから取り出した演算を使う第三者パッケージか, どれがやるかである. パッケージ間の責任の分割に一貫した方針をうち建てるのは, 多くのパッケージと多くの型のあるシステムでは, 苦難の事業であろう.
一般に, この考えを, 一つの型のオブジェクトを他の型の等価なオブジェクトに変更する強制型変換手続きを設計することで実装する. この代表的な強制型変換手続きは, 与えられた通常の数を, その実部と零の虚部を持つ複素数に変更する:
(define (scheme-number->complex n) (make-complex-from-real-imag (contents n) 0))この強制型変換手続きを, 二つの型で引く特別の強制型変換表に設定する:
(put-coercion 'scheme-number 'complex scheme-number->complex)(われわれはput-coercionとget-coercion手続きがこの表を操作するために使えると仮定する.) それぞれの型の任意のオブジェクトを, 他の型に強制変換するのは, 一般に可能ではないから, 一般に表のあるスロットは空であろう. 例えば任意の複素数を通常の数に強制変換する方法はないので, この表には一般的なcomplex->scheme-number手続きはない.
強制型変換の表が一旦出来ると, 2.4.3節のapply-generic手続きを修正することで, 強制型変換を画一的に扱うことが出来る. 演算を作用させようとすると, 以前のように, 引数の型に対する演算が定義されているか調べる. そうであれば演算対型の表で見つけた手続きに振り分ける. そうでなければ強制型変換を試みる. 単純にするため, 引数が二個の場合だけ考えよう. 50 強制型変換の表を調べ, 第一の型のオブジェクトが第二の型へ強制変換出来るかを見る. 出来るなら, 第一引数の型を強制変換し, 演算をもう一度試みる. 第一の型が一般に第二の型に強制変換出来なければ, 強制型変換を反対に調べ, 第二引数を第一引数の型に強制変換する方法はないか見る. 最後に, どちらの型ももう一方の型へ強制変換する既知の方法がなければ, 諦める. これが手続きだ:
(define (apply-generic op . args)
(let ((type-tags (map type-tag args)))
(let ((proc (get op type-tags)))
(if proc
(apply proc (map contents args))
(if (= (length args) 2)
(let ((type1 (car type-tags))
(type2 (cadr type-tags))
(a1 (car args))
(a2 (cadr args)))
(let ((t1->t2 (get-coercion type1 type2))
(t2->t1 (get-coercion type2 type1)))
(cond (t1->t2
(apply-generic op (t1->t2 a1) a2))
(t2->t1
(apply-generic op a1 (t2->t1 a2)))
(else
(error "No method for these types"
(list op type-tags))))))
(error "No method for these types"
(list op type-tags)))))))
強制型変換の方法は上に述べたように, 明示的に型の間の演算を定義する方法より多くの利点を持っている. 依然として型を関係づける手続き(n個の型を持つシステムには, 可能性としてはn2個の手続き)を書く必要はあるが, 型のそれぞれの対について一つの手続きを書けばよいので, 型と汎用演算の集りのそれぞれに別の手続きを書かなくてよい.51 われわれがここで期待するのは, 型の間の変換は型自身によるのであり, 作用させる演算にはよらないという事実である.
他方, 強制型変換の方式が十分に一般的でない応用もある. 統合しようとするオブジェクトのいずれもがもう一方の型に変換出来ない時でも, 両オブジェクトを第三の型へ変換することで, 演算を実行することが可能かも知れない. そういう複雑性を扱い, プログラムの部品化性を維持するためには, 次で論じるように, 型の間の関係の更なる構造の利点を使わなければならない.
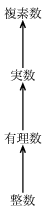
塔の構造があれば, 階層構造に新しい型を追加する問題は非常に単純化出来る. 新しい型はその上の拡大型のところにどう組み込まれ, 下の型のどういう拡大型であるかを指定するだけでよい. 例えば整数を複素数に足そうと思えば, 特別な強制型変換手続きinteger->complexを明示的に用意する必要はない. そうではなく, 整数をどう有理数へ変換し, 有理数をどう実数へ変換し, 実数をどう複素数へ変換するかを定義する. それからシステムに整数をこれらの段階を踏んで複素数へ変換させ, 二つの複素数を足させる.
apply-genericを次のように再設計する: 各型にはraise手続きを補わなくてはならない. それはその型のオブジェクトを塔の中で一レベル「高める」. システムが異る型のオブジェクトに演算させられる時, すべてのオブジェクトが塔の中で同じレベルになるまで, 低い方の型を順次高めることが出来る. (問題2.83と2.84は, この戦略の実装の詳細に関するものである.)
塔のもう一つの利点は, 各型が拡大型で定義されたすべての演算を「継承する」考え方を容易に実装出来ることだ. たとえば, 整数の実部を探す特別な手続きを補わなくても, 整数が複素数の部分型であるため, 整数に対してreal-partが定義出来るであろうと期待出来る. 塔があれば, apply-genericを修正することで, こういうことが画一的に出来るようになる. 要求された演算が与えられたオブジェクトに直接定義してなくても, オブジェクトを拡大型に高め, もう一度試みる. われわれはこうして塔を登り, それに従って引数を変換し, ついには望みの演算が実行出来るレベルが見つかるか, 塔頂に達する(その時は諦める)かである.
より一般的な階層構造に比べ, 塔の更にもう一つの利点は, データオブジェクトを最簡な表現にまで「降ろす」単純な方法があることだ. 例えば2 + 3iと4 - 3iを足すと, 答が複素数6 + 0iではなく, 整数6になると嬉しい. 問題2.85は下降演算を実装する方法を論じている. (6 + 0iのような下降出来るオブジェクトを, 6 + 2iのような下降出来ないものから区別する一般的方法を必要とするのがトリックである.)

図2.26 幾何学図形の型の間の関係
(define (scheme-number->scheme-number n) n)
(define (complex->complex z) z)
(put-coercion 'scheme-number 'scheme-number
scheme-number->scheme-number)
(put-coercion 'complex 'complex complex->complex)
としようとする. (define (exp x y) (apply-generic 'exp x y))が定義してあり, scheme数パッケージのべき乗の手続き
;; 次はScheme数パッケージへ追加する
(put 'exp '(scheme-number scheme-number)
(lambda (x y) (tag (expt x y)))) ; 基本手続きexptを使う.
はあるが, 他のパッケージにはないとしよう. 引数に二つの複素数を持ってexpを呼び出すと何が起きるか.
49
殆んど同じ手続きで(scheme-number complex)を扱う手続きも用意しなければならない.
50
一般化については, 問題2.82参照
51
うまくやればn2個より少ない強制変換の手続きで済ませられる. 例えば型1から型2への変換法と, 型2
から型3への変換法を知っていれば, この知識を使って型1から型3へ変換出来る. これは新しい型をシステムに追加した時, 積極的に補わなければならない強制型変換手続きの数を格段に減らす. われわれがシステムに必要な限りの技巧を組み込もうとするなら, 型の間の関係の「グラフ」を探させ, 明示的に与えられたものから推論出来る, 強制型変換手続きを自動的に生成させられる.
52
本書の第一版にもあったこの記述は, 十二年前に書いた時に真であったのと同様に, 今でも真である. ものの異る型の間の関係を表す, 有用で一般的な(哲学者が「存在論」と呼ぶ)枠組を開発することは, 扱い難いまでに難しい. 十年前に存在した混乱と, 今存在する混乱との違いは, 今では多くの不十分な存在論上の理論が, 対応した不十分なプログラム言語の多くの中に具体化されていることである. 例えば
オブジェクト指向プログラミング言語の複雑さの多くは---そして現今のオブジェクト指向言語間の微妙で混乱させるような差異は---相互に関係する型の汎用演算の扱いに集中している. 3章の計算オブジェクトに関するわれわれの議論は, こういう論点を全く避けている. オブジェクト指向プログラミングに精通している読者は, われわれが3章において, 局所状態については多くを語るが, 「クラス」や「継承」については語らないことに気がつくであろう. 実際われわれは, この問題は知識表現や自動推論の研究に頼らず, 計算機言語の設計だけでは適切には語れないと思う.
53
実数は整数へ, 引数に最も近い整数を返す
round手続きを使って投影することが出来る.